Unitary representation
of a topological group
A representation of the topological group by unitary operators in a Hilbert space (cf. Unitary operator). The theory of unitary representations is one of the most developed parts of the theory of representations of topological groups, which is connected both with its numerous applications and with the presence of a number of properties facilitating the study of unitary representations. Thus, any unitary representation is completely reducible; for a unitary representation the conditions of complete irreducibility, tensor irreducibility, topological irreducibility, and operator irreducibility are all equivalent; from the continuity of a unitary representation with respect to the weak operator topology follows its continuity with respect to the strong operator topology; for a unitary representation one can define the operation of tensor product of representations, as well as the operation of passing to the contragredient representation (in the Hilbert space which is the complex conjugate of the given one), and for the operations of direct sum, tensor product and passing to the contragredient representation there hold a number of natural algebraic relations.
The most highly developed part of the general theory of unitary representations and the most important in applications is the theory of unitary representations of locally compact groups. There does not exist a description of the class of groups for which the unitary representations (or the irreducible unitary representations) separate the points of the group (1992). However, if the group $ G $ is locally compact, then for every non-identity element $ g \in G $ there exists an irreducible unitary representation $ \pi $ of $ G $ such that $ \pi ( g) $ is a non-identity operator in the space of the representation (the Gel'fand–Raikov theorem). Further, between the non-degenerate symmetric representations of the group algebra $ L _ {1} ( G) $( constructed with the left Haar measure) and the continuous unitary representations of the group $ G $ there exists a natural one-one correspondence $ \pi ^ \prime \mapsto \pi $, defined by the formula
$$ \pi ^ \prime ( f ) = \ \int\limits _ { G } f ( y) \pi ( g) dm ( g),\ \ f \in L _ {1} ( G); $$
moreover, the representation $ \pi ^ \prime $ of the algebra $ L _ {1} ( G) $ is topologically irreducible (is a quotient representation, a representation of a given type, a representation equivalent or quasi-equivalent to another) if and only if the corresponding unitary representation $ \pi $ of the group has the same property.
The theory of cyclic unitary representations of a locally compact group $ G $, which is related to the theory of positive linear functionals on $ L _ {1} ( G) $, may be studied by means of appropriate spherical functions (cf. Representation of a topological group). The spherical functions connected with unitary representations of a locally compact group $ G $ are continuous positive-definite functions on the group, and, conversely, any continuous positive-definite function on $ G $, equal to 1 at the identity, is a spherical function connected with a cyclic unitary representation (and defined by the cyclic vector of this unitary representation). The set $ B ( G) $ of all linear combinations of continuous positive-definite functions on $ G $ forms a commutative Banach algebra (relative to the usual multiplication), called the Fourier–Stieltjes algebra of $ G $; the closed ideal $ A ( G) $ in $ B ( G) $ generated by the functions of the form $ \phi ^ {*} \psi $, where $ \phi , \psi \in L _ {2} ( G) $, is called the Fourier algebra of $ G $. The Banach algebras $ A ( G) $ and $ B ( G) $ define the group $ G $ up to an isomorphism or anti-isomorphism.
On the set $ P _ {1} $ of continuous positive-definite functions on $ G $, equal to 1 at the unit element of the group, the topology of uniform convergence on compact subsets of $ G $ coincides with the weak topology defined by the duality between $ L _ {1} ( G) $ and $ L _ \infty ( G) $ and the imbedding of $ P _ {1} $ in $ L _ \infty ( G) $. Any function $ \phi $ in $ P _ {1} $ is the limit (in this topology) of a net of convex combinations of positive-definite functions, connected with irreducible unitary representations of $ G $; if further $ G $ is a separable group, then there exists a positive measure $ \mu _ \phi $ on the compact set of continuous positive-definite functions on $ G $, not exceeding 1 in absolute value, concentrated on $ P _ {1} $ and such that
$$ \phi ( g) = \ \int\limits _ {P _ {1} } \chi ( g) d \mu _ \phi ( \chi ) \ \textrm{ for } \textrm{ all } g \in G. $$
The construction of unitary representations from positive-definite functions allows a generalization to the case of positive-definite measures on $ G $. If $ G $ is a separable group, then any representation defined by a positive-definite measure is cyclic.
A unitary representation $ \pi $ of a locally compact group $ G $ in a Hilbert space $ H $ admits a decomposition as a topological direct integral of irreducible unitary representations of $ G $, if either $ G $ or $ H $ is separable (for non-separable groups and spaces this is not generally true). Moreover, in this case the unitary representation $ \pi $ admits an essentially unique decomposition as a direct integral of quotient representations. In connection with this fact an essential role is played by the dual space $ \widehat{G} $( the quotient space of the space of irreducible unitary representations of $ G $, considered with the topology defined by uniform convergence of matrix entries on compact sets and with the Borel structure subordinate to this topology, with respect to the equivalence defined by unitary equivalence of unitary representations) and the quasi-dual space $ \widetilde{G} $( the quotient space of the space of quotient representations of $ G $, considered with the Borel structure subordinate to the topology of uniform convergence of matrix entries on compact sets). Thus, $ \widehat{G} $ is a topological and a Borel space, and $ \widetilde{G} $ is a Borel space, which for a separable group may be equipped with the topology extending the topology on $ \widehat{G} $. The group $ G $ is said to be a group of type I if all its quotient representations are of type I; for such groups questions of the theory of unitary representations can be solved more simply than in the general case. Groups of type I include algebraic Lie groups and algebraic Chevalley groups over $ p $- adic fields, nilpotent Lie groups, and others. A characterization of the simply-connected solvable Lie groups of type I is known. A group $ G $ is called a CCR-group if for any irreducible unitary representation $ \pi $ of $ G $ the image $ \widetilde \pi ( L _ {1} ( G)) $ under the representation $ \widetilde \pi $ is contained in the set $ \mathop{\rm BC} ( H _ \pi ) $ of compact operators in the space $ H _ \pi $ of the representation $ \pi $. Every CCR-group is of type I. A group of type I is a CCR-group if and only if its dual space is a $ T _ {1} $- space. Nilpotent Lie groups and linear semi-simple Lie groups are CCR-groups. The image of the representation $ ( \pi \otimes \sigma ) \widehat{ {}} $ is contained in $ \mathop{\rm BC} ( H _ {\pi \otimes \sigma } ) $ for all irreducible unitary representations $ \pi , \sigma $ of $ G $ if and only if all irreducible unitary representations are finite-dimensional.
A separable locally compact group is of type I if and only if its dual space satisfies the separation axiom $ T _ {0} $. Other topological properties of the spectra ( $ T _ {1} $- separation, the Hausdorff property, discreteness, and others) are also connected with properties of the group. A particularly close link between the topological and algebraic properties of the group and its dual space exists in classes of groups satisfying various compactness conditions. Among these classes of locally compact groups are included: 1) the class $ [ \mathop{\rm MAP} ] $ of maximal almost-periodic groups (admitting a continuous imbedding in a compact group); 2) the class $ [ \mathop{\rm SIN} ] $ of groups containing a fundamental system of neighbourhoods of the unit element that are invariant under inner automorphisms; 3) the class $ [ \mathop{\rm FC} ] ^ {-} $ of groups with pre-compact classes of conjugate elements; 4) the class $ [ \mathop{\rm FIA} ] ^ {-} $ of groups with a pre-compact group of inner automorphisms; 5) the class $ [ \mathop{\rm FIR} ] \subset [ \mathop{\rm MAP} ] \cap [ \mathop{\rm SIN} ] $ of groups all irreducible unitary representations of which are finite-dimensional; and 6) the class $ [ Z] \subset [ \mathop{\rm FIR} ] $ of groups whose quotient group by the centre is compact. The dual spaces of groups of class $ [ \mathop{\rm FC} ] ^ {-} $ are Hausdorff spaces, and a group of class $ [ \mathop{\rm FIR} ] $ is discrete if and only if its dual space is compact (though not necessarily separable). The theory of unitary representations of groups of class $ [ \mathop{\rm MAP} ] $ is connected with the theory of almost-periodic functions on locally compact groups.
The character of a unitary representation of a locally compact group $ G $ is the faithful normal semi-finite trace $ t $( cf. Trace on a $ C ^ {*} $- algebra) on the set of positive elements of the von Neumann algebra $ \mu _ \pi $ generated by the family $ \pi ( G) $, such that the set of elements $ x $ of the group $ C ^ {*} $- algebra $ C ^ {*} ( G) $ of $ G $( the enveloping $ C ^ {*} $- algebra of the group algebra $ L _ {1} ( G) $) for which $ t ( \pi ( x ^ {*} , x)) $ is finite, goes over into the set generated by the von Neumann algebra $ \pi ( G) ^ {\prime\prime} $. If $ \pi $ is a quotient representation (respectively, an irreducible unitary representation), then the character $ t $ defines the unitary representation $ \pi $ uniquely up to a quasi-equivalence (respectively, an equivalence). If $ \pi _ {1} $, $ \pi _ {2} $ are irreducible unitary representations of $ G $ with characters $ t _ {1} $, $ t _ {2} $, respectively, then the product of these traces defines a trace on the von Neumann algebra induced by the unitary representation $ \pi _ {1} \otimes \pi _ {2} $. If this trace is the character of the representation $ \pi _ {1} \otimes \pi _ {2} $, then (for separable groups or separable representation spaces) it defines a decomposition of the unitary representation $ \pi _ {1} \otimes \pi _ {2} $ into a direct integral of quotient representations with a trace with respect to a uniquely defined measure (the Plancherel measure for $ \pi _ {1} \otimes \pi _ {2} $) on the quasi-spectrum $ \widetilde{G} $. The determination of the Plancherel measure on the tensor product of unitary representations is one of the general problems in the theory of unitary representations; in a number of cases (in particular, for the groups $ \mathop{\rm SL} ( 2, \mathbf C ) $, $ \mathop{\rm SL} ( 2, \mathbf R ) $, certain unitary representations of other semi-simple Lie groups, and certain solvable Lie groups) this problem has been solved (using the spectral decomposition of the Laplace operator, the orbit method or the horosphere method).
Sometimes one understands by the character of a unitary representation $ \pi $ in a Hilbert space $ H $ a linear functional $ \chi \pi $ on a translation-invariant subalgebra $ D _ \pi ( G) $ of $ M ( G) $, defined by the equation $ \chi \pi ( a) = \mathop{\rm Tr} \widetilde \pi ( a) $, $ a \in D _ \pi ( G) $, where $ \widetilde \pi $ is the representation of $ D _ \pi ( G) $ defined by $ \pi $( assuming that $ \pi $ is uniquely determined by the representation $ \widetilde \pi $, the operators of $ \widetilde \pi $ are nuclear and the mapping $ \widetilde \pi $ of the algebra $ D _ \pi ( G) $ into the space of nuclear operators is continuous). The characters of irreducible unitary representations of semi-simple and nilpotent Lie groups are defined by generalized functions, which in the case of semi-simple groups are measurable and locally integrable. The characters of irreducible unitary representations of solvable Lie groups of type I are defined, generally speaking, only on a subalgebra of the algebra $ C _ {0} ^ \infty ( G) $ of infinitely-differentiable functions on $ G $ with compact support. In general, the calculation of the characters is based on formulas for the characters of induced representations.
A compact subgroup $ K $ of a group $ G $ is called rich (or massive) if the restriction of any unitary representation $ \pi $ of $ G $ to $ K $ contains any irreducible unitary representation $ \sigma $ of $ K $ with finite multiplicity. Let $ P _ \sigma ^ \pi $ be the projector from the space $ H _ \pi $ of the representation $ \pi $ onto the subspace on which that representation of $ K $ acts which is a multiple of $ \sigma $; the functions of the form
$$ \phi _ \sigma ^ \pi ( g) = \ \mathop{\rm Tr} ( P _ \sigma ^ \pi \pi ( g) ) ,\ \ g \in G, $$
are called $ K $- spherical functions of the representation $ \pi $( cf. Representation function). A group $ G $ with a rich compact subgroup is of type I; every irreducible unitary representation of $ G $ has a character and is defined uniquely up to an equivalence by any non-zero spherical function; the dual space $ \widehat{G} $ of the group $ G $ can be expressed as a countable union of (intersecting) locally compact Hausdorff spaces (describing the $ \pi \in \widehat{G} $ for which $ \phi _ \sigma ^ \pi = 0 $ for a given $ \sigma \in \widehat{K} _ \pi $, and the dimension of the corresponding projector $ P _ \sigma ^ \pi $ has a given value). The linear semi-simple Lie groups and the $ [ Z] $- groups are groups with rich compact subgroups.
Let $ \pi $ be a unitary representation of a group $ G $ in a Hilbert space $ H $, and let $ M _ \pi $ be the von Neumann algebra generated by the family $ \pi ( G) $. The representation $ \pi $ is said to be trace-admissible if there exists a trace on $ M _ \pi ^ {+} $ which is a character for $ \pi $. By a trace on the group $ G $ one understands a semi-finite lower semi-continuous trace on $ C ^ {*} ( G) ^ {+} $; a trace on $ G $ is called a character of $ G $ if the corresponding unitary representation of $ G $ is a quotient representation. There is a canonical one-to-one correspondence between the set of characters of $ G $, defined up to a positive factor, and the set of quasi-equivalence classes of trace-admissible quotient representations of $ G $; moreover, a quotient representation of finite type corresponds to a continuous central positive-definite function on $ G $.
The regular representation of a locally compact group $ G $ in the Hilbert space $ L _ {2} ( G) $ is a faithful continuous unitary representation; the $ C ^ {*} $- algebra generated by the image of the corresponding representation of the algebra $ L _ {1} ( G) $ is called the reduced $ C ^ {*} $- algebra of the group $ G $ and is denoted by $ C _ {r} ^ {*} ( G) $; let $ N $ be the kernel of the canonical epimorphism of $ C ^ {*} ( G) $ onto $ C _ {r} ^ {*} ( G) $ defined by the regular representation. The group $ G $ is amenable, i.e. there is an invariant mean on $ L _ \infty ( G) $, if and only if $ N = \{ 0 \} $( bounded representations of amenable groups in a Hilbert space are equivalent to unitary representations). The family of unitary representations $ \pi \in \widehat{G} $ for which the kernel of the corresponding representation of $ C ^ {*} ( G) $ contains $ N $ is called the fundamental series. The remaining unitary representations $ \pi \in \widehat{G} $ form the supplementary series.
Let $ G $ be a unimodular separable locally compact group of type I, and let $ W ^ {*} ( G) $ be the von Neumann algebra $ \mu _ \lambda $, where $ \lambda $ is the regular unitary representation of $ G $. There exists a unique positive measure $ \overline \mu \; $ on the spectrum $ \widehat{G} $ of $ G $ satisfying the condition
$$ \tag{* } \int\limits _ { G } | f ( g) | ^ {2} d \mu ( g) = \ \int\limits _ {\widehat{G} } \mathop{\rm Tr} ( \pi ( f ) \pi ( f ) ^ {*} ) d \widehat \mu ( \pi ) $$
for all $ f \in L _ {1} ( G) \cap L _ {2} ( G) $. The measure $ \widehat \mu $ is called the Plancherel measure. Further, there exists an isomorphism of the space $ L _ {2} ( G) $ onto a direct integral of Hilbert–Schmidt operators in the space of the representation $ \pi \in \widehat{G} $ with respect to the measure $ \widehat \mu $, which transforms the left-regular unitary representation $ \lambda $ into a direct integral of unitary representations that are multiples of $ \pi $, and transforms the trace on $ W ^ {*} ( G) $ defined by the trace $ {\mathcal E} _ {e} $ on $ G $( $ {\mathcal E} _ {e} ( f ) = f( e) $ for $ f \in K ( G) $) into the direct integral of traces, $ T \otimes 1 \rightarrow \mathop{\rm Tr} T $ on $ ( \mu \otimes C _ {1} ) ^ {+} $. The trace $ {\mathcal E} _ {e} $ on $ C ^ {*} ( G) ^ {+} $ coincides with the trace $ f \rightarrow \int _ {\widehat{G} } \mathop{\rm Tr} \pi ( f ) d \widehat \mu ( \pi ) $, $ f \in C ^ {*} ( G) $. The formula (*) is called the Plancherel formula; it admits a generalization to non-separable unimodular locally compact groups of type I, as well as to non-unimodular separable locally compact groups and separable groups not of type I. One of the tasks of the theory of unitary representations is the explicit construction of a Plancherel measure for a given locally compact group. This problem has only been partly solved (for example, for semi-simple real Lie groups, for solvable Lie groups of type I, as well as for certain groups of motions, certain Chevalley groups, and certain groups satisfying a compactness condition). The decomposition of the regular unitary representation and the Plancherel formula are connected with the theory of square-integrable representations, discrete series (of representations) and integrable representations (cf. Integrable representation).
A complete description of the irreducible unitary representations of locally compact groups is unknown, even in the case of Lie groups. It has been obtained only for solvable Lie groups of type I, certain reductive Lie groups, as well as for Chevalley groups (of low dimensions), certain nilpotent locally compact Lie groups and certain semi-direct products. In this description a decisive role is played by the inducing operator (and its generalizations); in particular, the orbit method (and its generalizations). The problem of studying more general projective unitary representations and unitary representations with multipliers is connected with the theory of ordinary unitary representations by means of the theory of (continuous or Borel) cohomology groups. For groups that are not of type I a complete description of the quotient representations (up to a quasi-equivalence) does not exist, although for some of them a description of the quotient representations of finite type has been obtained.
The theory of unitary representations plays a fundamental role in the theory of series on (Banach and topological) group algebras: in the study of Wiener properties and complete symmetry, in the description of the maximal one-sided and two-sided ideals, etc. The theory of unitary representations plays an important role, also, in questions of representation theory and harmonic analysis, requiring a use of non-unitary representations — as in the construction of the bounded series and the supplementary series; in the definition of operators in explicit form; in splitting representations from the analytic continuation of the basic series of unitary representations; in the study of intertwining of completely-reducible representations; in the development of harmonic analysis in function spaces on groups and homogeneous spaces other than the space $ L _ {2} $; and in the study on the structure and properties of group algebras (measure algebras, the algebra $ L _ {1} ( G) $, the topological algebra $ K ( G) $).
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | A.I. Shtern, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [3] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [4] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [5] | D.P. Zhelobenko, A.I. Shtern, "Representations of Lie groups" , Moscow (1983) (In Russian) |
| [6] | J. Dixmier, "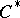 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [7] | I.M. Gel'fand, M.I. Graev, I.I. Pyatetskii-Shapiro, "Generalized functions" , 6. Representation theory and automorphic functions , Saunders (1969) (Translated from Russian) |
| [8] | N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [9] | A.O. Barut, R. Raçzka, "Theory of group representations and applications" , 1–2 , PWN (1977) |
| [10] | A.U. Klimyk, "Matrix elements and Clebsch–Gordan coefficients of group representations" , Kiev (1979) (In Russian) |
| [11] | G.W. Mackey, "Unitary group representations in physics, probability and number theory" , Benjamin/Cummings (1978) |
| [12] | P. Bernal, et al., "Répresentation des groupes de Lie résolubles" , Dunod (1972) |
| [13] | J. Brezin, "Harmonic analysis on compact solvmanifolds" , Springer (1977) |
| [14] | G. Carmona (ed.) M. Vergne (ed.) , Non-commutative harmonic analysis (Marseille, 1978) , Lect. notes in math. , 728 , Springer (1979) |
Comments
See also (the editorial comments to) Representation function and Spherical functions for another usage of the term "spherical function" . In [8] and [a1] a subgroup $ H $ of $ G $ is called massive if the trivial representation of $ H $ occurs with multiplicity at most $ 1 $ in each irreducible representation of $ G $. See [8], [10] and [a1] for interpretations of special functions as matrix elements of unitary representations.
References
| [a1] | N.Ya. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , 1 , Kluwer (1991) (Translated from Russian) |
Unitary representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_representation&oldid=49085