Tate module
A free $ \mathbf Z _ {p} $-
module $ T ( G) $
associated to a $ p $-
divisible group $ G $
defined over a complete discrete valuation ring $ R $
of characteristic 0 with residue field $ k $
of characteristic $ p $.
Let $ G = \{ G _ \nu , i _ \nu \} $,
$ \nu \geq 0 $,
and $ T ( G) = \lim\limits _ \leftarrow G _ \nu ( \overline{K}\; ) $,
where $ \overline{K}\; $
is the algebraic closure of the quotient field $ K $
of the ring $ R $;
the limit is taken with respect to the mappings $ j _ \nu : G _ {\nu + 1 } \rightarrow G _ \nu $
for which $ i _ \nu \circ j _ \nu = p $.
Then $ T ( G) = \mathbf Z _ {p} ^ {h} $,
where $ h $
is the height of the group $ G $
and $ T ( G) $
has the natural structure of a $ G ( \overline{K}\; /K) $-
module. The functor $ G \rightarrow T ( G) $
allows one to reduce a number of questions about the group $ G $
to simpler questions about $ G ( \overline{K}\; /K) $-
modules.
The Tate module is defined similarly for an Abelian variety. Let $ A $ be an Abelian variety defined over $ k $, and let $ A _ {p ^ {n} } $ be the group of points of order $ p ^ {n} $ in $ A ( \overline{k}\; ) $. Then $ T ( A) $ is defined as $ \lim\limits _ \leftarrow A _ {p ^ {n} } $. The Tate module of a curve $ X $ is the Tate module of its Jacobi variety.
The construction of the module $ T _ {p} ( X) $ can be extended to number fields. Let $ K $ be an algebraic number field and let $ k _ \infty $ be a $ \mathbf Z _ {p} $- extension of the field $ k $( an extension with Galois group isomorphic to $ \mathbf Z _ {p} $). For the intermediate field $ k _ {n} $ of degree $ p ^ {n} $ over $ k $, let $ \mathop{\rm Cl} ( k _ {n} ) _ {p} $ be the $ p $- component of the ideal class group of the field $ k _ {n} $. Then $ T _ {p} ( k _ \infty ) = \lim\limits _ \leftarrow \mathop{\rm Cl} ( k _ {n} ) _ {p} $, where the limit is taken with respect to norm-mappings $ \mathop{\rm Cl} ( k _ {m} ) _ {p} \rightarrow \mathop{\rm Cl} ( k _ {n} ) _ {p} $ for $ m > n $. The module $ T _ {p} ( k _ \infty ) $ is characterized by its Iwasawa invariants $ \lambda $, $ \mu $ and $ \nu $, defined by
$$ | \mathop{\rm Cl} ( k _ {n} ) _ {p} | = \ p ^ {e _ {n} } , $$
where $ e _ {n} = \lambda n + \mu p ^ {n + \nu } $ for all sufficiently large $ n $. For cyclotomic $ \mathbf Z _ {p} $- extensions the invariant $ \mu $ is equal to 0. This was also proved for Abelian fields [4]. Examples are known of non-cyclotomic $ \mathbf Z _ {p} $- extensions with $ \mu > 0 $( see [3]). Even in the case when $ \mu = 0 $, $ T _ {p} ( k _ \infty ) $ is not necessarily a free $ \mathbf Z _ {p} $- module.
References
| [1] | J.T. Tate, "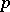 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 |
| [2] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [3] | K. Iwasawa, "On the 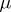 -invariants of -invariants of 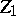 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 |
| [4] | B. Ferrero, L.C. Washington, "The Iwasawa invariant 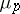 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 |
Tate module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tate_module&oldid=48951