Quasi-equivalent representations
Two unitary representations (cf. Unitary representation) $ \pi _ {1} , \pi _ {2} $
of a group $ X $(
or symmetric representations of a symmetric algebra $ X $)
in Hilbert spaces $ H _ {1} $
and $ H _ {2} $,
respectively, satisfying one of the following four equivalent conditions: 1) there exist unitarily-equivalent representations $ \rho _ {1} $
and $ \rho _ {2} $
such that $ \rho _ {1} $
is a multiple of $ \pi _ {1} $
and $ \rho _ {2} $
is a multiple of $ \pi _ {2} $;
2) the non-zero subrepresentations of $ \pi _ {1} $
are not disjoint from $ \pi _ {2} $,
and the non-zero subrepresentations of $ \pi _ {2} $
are not disjoint from $ \pi _ {1} $;
3) $ \pi _ {2} $
is unitarily equivalent to a subrepresentation of some multiple representation $ \rho _ {1} $
of $ \pi _ {1} $
that has unit central support; or 4) there exists an isomorphism $ \Phi $
of the von Neumann algebra generated by the set $ \pi _ {1} ( X) $
onto the von Neumann algebra generated by the set $ \pi _ {2} ( X) $
such that $ \Phi ( \pi _ {1} ( x) ) = \pi _ {2} ( x) $
for all $ x \in X $.
Unitarily-equivalent representations are quasi-equivalent representations; irreducible quasi-equivalent representations (cf. Irreducible representation) are unitarily equivalent. If $ \pi _ {1} $
and $ \pi _ {2} $
are quasi-equivalent representations and $ \pi _ {1} $
is a factor representation, then so is $ \pi _ {2} $;
a factor representation and a non-zero subrepresentation of it are quasi-equivalent representations; two factor representations are either disjoint or quasi-equivalent. The notion of quasi-equivalent representations leads to that of a quasi-dual object and a quasi-spectrum for locally compact groups and symmetric algebras, respectively.
References
| [1] | J. Dixmier, "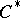 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Comments
Two representations $ \pi $ and $ \pi ^ \prime $( of a group or algebra) with representation spaces $ H $ and $ H ^ \prime $, respectively, are said to be disjoint is there is no non-zero intertwining operator between $ \pi $ and $ \pi ^ \prime $. Here, an intertwining operator between $ \pi $ and $ \pi ^ \prime $ is a continuous linear operator $ T : H \rightarrow H ^ \prime $ such that $ T \pi ( x) = \pi ^ \prime T ( x) $ for all $ x $.
Quasi-equivalent representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-equivalent_representations&oldid=48381