Difference between revisions of "Zygmund class of functions"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | z0993401.png | ||
| + | $#A+1 = 31 n = 1 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/Z099/Z.0909340 Zygmund class of functions | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ M $ | |
| + | be a positive real number. The Zygmund class $ Z _ {M} $ | ||
| + | is the class of continuous $ 2 \pi $- | ||
| + | periodic functions $ f $ | ||
| + | with the property that for all $ x $ | ||
| + | and all $ h > 0 $ | ||
| + | the inequality | ||
| − | + | $$ | |
| + | | f ( x + h ) - 2f ( x) + f ( x - h ) | \leq M h | ||
| + | $$ | ||
| − | + | holds. The class $ Z _ {M} $ | |
| + | was introduced by A. Zygmund [[#References|[1]]]. In terms of this class one can obtain a conclusive solution to the Jackson–Bernstein problem on direct and inverse theorems in the theory of approximation of functions (cf. [[Bernstein theorem|Bernstein theorem]]; [[Jackson theorem|Jackson theorem]]). For example: A continuous $ 2 \pi $- | ||
| + | periodic function $ f $ | ||
| + | belongs to the Zygmund class $ Z _ {M} $ | ||
| + | for some $ M > 0 $ | ||
| + | if and only if its best uniform approximation error $ E _ {n} ( f ) $ | ||
| + | by trigonometric polynomials of degree $ \leq n $ | ||
| + | satisfies the inequality | ||
| − | + | $$ | |
| + | E _ {n} ( f ) \leq | ||
| + | \frac{A}{n} | ||
| + | , | ||
| + | $$ | ||
| − | in which the constant | + | where $ A > 0 $ |
| + | is a constant. The modulus of continuity $ \omega ( \delta , f ) $ | ||
| + | of any function $ f \in Z _ {M} $ | ||
| + | admits the estimate | ||
| + | |||
| + | $$ | ||
| + | \omega ( \delta , f ) \leq | ||
| + | \frac{M}{2 \mathop{\rm ln} \sqrt {2 } + 1 } | ||
| + | |||
| + | \delta \mathop{\rm ln} | ||
| + | \frac \pi \delta | ||
| + | + O ( \delta ) | ||
| + | $$ | ||
| + | |||
| + | in which the constant $ M / 2 \mathop{\rm ln} ( \sqrt {2 } + 1 ) $ | ||
| + | cannot be improved on for the entire class $ Z _ {M} $[[#References|[3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Zygmund, "Smooth functions" ''Duke Math. J.'' , '''12''' : 1 (1945) pp. 47–76 ((Also: Selected papers of Antoni Zygmund, Vol. 2, Kluwer, 1989, pp. 184–213.))</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.V. Efimov, "Estimation of the modules of continuity of functions of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z099/z099340/z09934022.png" />" ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''21''' : 2 (1957) pp. 283–288 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Zygmund, "Smooth functions" ''Duke Math. J.'' , '''12''' : 1 (1945) pp. 47–76 ((Also: Selected papers of Antoni Zygmund, Vol. 2, Kluwer, 1989, pp. 184–213.))</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.V. Efimov, "Estimation of the modules of continuity of functions of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z099/z099340/z09934022.png" />" ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''21''' : 2 (1957) pp. 283–288 (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
The quantity | The quantity | ||
| − | + | $$ | |
| + | \omega _ {f} ^ {*} ( h) = \sup _ { x } | ||
| + | \sup _ {| \delta | \leq n } \ | ||
| + | | f( x+ \delta ) - 2f( x) + f( x- \delta ) | , | ||
| + | $$ | ||
| − | for a | + | for a $ 2 \pi $- |
| + | periodic function $ f $, | ||
| + | is its Zygmund modulus. In terms of this, Zygmund's theorem above can also be stated as: A $ 2 \pi $- | ||
| + | periodic function $ f $ | ||
| + | satisfies $ E _ {n} ( f ) \leq n ^ {-} 1 A $ | ||
| + | for some $ A $ | ||
| + | if and only if $ \omega _ {f} ^ {*} ( h ) \leq Bh $( | ||
| + | $ h > 0 $) | ||
| + | for some $ B $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff</TD></TR></table> | ||
Revision as of 08:30, 6 June 2020
Let $ M $
be a positive real number. The Zygmund class $ Z _ {M} $
is the class of continuous $ 2 \pi $-
periodic functions $ f $
with the property that for all $ x $
and all $ h > 0 $
the inequality
$$ | f ( x + h ) - 2f ( x) + f ( x - h ) | \leq M h $$
holds. The class $ Z _ {M} $ was introduced by A. Zygmund [1]. In terms of this class one can obtain a conclusive solution to the Jackson–Bernstein problem on direct and inverse theorems in the theory of approximation of functions (cf. Bernstein theorem; Jackson theorem). For example: A continuous $ 2 \pi $- periodic function $ f $ belongs to the Zygmund class $ Z _ {M} $ for some $ M > 0 $ if and only if its best uniform approximation error $ E _ {n} ( f ) $ by trigonometric polynomials of degree $ \leq n $ satisfies the inequality
$$ E _ {n} ( f ) \leq \frac{A}{n} , $$
where $ A > 0 $ is a constant. The modulus of continuity $ \omega ( \delta , f ) $ of any function $ f \in Z _ {M} $ admits the estimate
$$ \omega ( \delta , f ) \leq \frac{M}{2 \mathop{\rm ln} \sqrt {2 } + 1 } \delta \mathop{\rm ln} \frac \pi \delta + O ( \delta ) $$
in which the constant $ M / 2 \mathop{\rm ln} ( \sqrt {2 } + 1 ) $ cannot be improved on for the entire class $ Z _ {M} $[3].
References
| [1] | A. Zygmund, "Smooth functions" Duke Math. J. , 12 : 1 (1945) pp. 47–76 ((Also: Selected papers of Antoni Zygmund, Vol. 2, Kluwer, 1989, pp. 184–213.)) |
| [2] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [3] | A.V. Efimov, "Estimation of the modules of continuity of functions of class 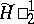 " Izv. Akad. Nauk. SSSR Ser. Mat. , 21 : 2 (1957) pp. 283–288 (In Russian) " Izv. Akad. Nauk. SSSR Ser. Mat. , 21 : 2 (1957) pp. 283–288 (In Russian) |
Comments
The quantity
$$ \omega _ {f} ^ {*} ( h) = \sup _ { x } \sup _ {| \delta | \leq n } \ | f( x+ \delta ) - 2f( x) + f( x- \delta ) | , $$
for a $ 2 \pi $- periodic function $ f $, is its Zygmund modulus. In terms of this, Zygmund's theorem above can also be stated as: A $ 2 \pi $- periodic function $ f $ satisfies $ E _ {n} ( f ) \leq n ^ {-} 1 A $ for some $ A $ if and only if $ \omega _ {f} ^ {*} ( h ) \leq Bh $( $ h > 0 $) for some $ B $.
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff |
Zygmund class of functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zygmund_class_of_functions&oldid=49251