Zarankiewicz crossing number conjecture
Turán brick factory problem
P. Turán [a6] tells about how he posed the following problem while in a forced labour camp in World War II: "There were some kilns where the bricks were made and some open storage yards where the bricks were stored. All the kilns were connected by rail with all storage yards. … the trouble was only at crossings. The trucks generally jumped the rails there, and the bricks fell out of them; in short this caused a lot of trouble and loss of time … the idea occurred to me that this loss of time could have been minimized if the number of crossings of the rails had been minimized. But what is the minimum number of crossings?"
Recall that a drawing of a finite graph 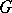 on the plane consists of placing the vertices of
on the plane consists of placing the vertices of 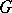 on the plane and drawing the edges of
on the plane and drawing the edges of 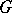 using continuous curves of the plane, connecting corresponding vertices as endpoints of the curve such that no curve has a vertex as an internal point and no point is an internal point of
using continuous curves of the plane, connecting corresponding vertices as endpoints of the curve such that no curve has a vertex as an internal point and no point is an internal point of  curves. The crossing number
curves. The crossing number 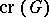 of a graph
of a graph 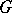 is the minimum number of intersection points among the curves representing edges, over all possible drawings of the graph. It is not hard to see that the crossing number can always be realized by a drawing with the following properties:
is the minimum number of intersection points among the curves representing edges, over all possible drawings of the graph. It is not hard to see that the crossing number can always be realized by a drawing with the following properties:
i) there is no self-crossing of edges;
ii) edges with the same endpoint do not cross;
iii) intersection points among the curves representing edges are crossing points, i.e. the curves do not touch each other; and
iv) any two edges intersect at most once. For variations in the definition of crossing numbers, see [a1].
Put in the technical terms above, Zarankiewicz' crossing number conjecture, or Turán's brick factory problem, is as follows: "what is the crossing number crKn,m of the complete bipartite graph Kn,m?"
Place 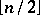 vertices to negative positions on the
vertices to negative positions on the  -axis,
-axis, 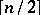 vertices to positive positions on the
vertices to positive positions on the  -axis,
-axis, 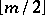 vertices to negative positions on the
vertices to negative positions on the 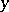 -axis,
-axis, 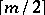 vertices to positive positions on the
vertices to positive positions on the 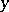 -axis, and draw
-axis, and draw 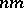 edges by straight line segments to obtain a drawing of
edges by straight line segments to obtain a drawing of 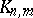 . It is not hard to check that the following formula gives the number of crossings in this particular drawing:
. It is not hard to check that the following formula gives the number of crossings in this particular drawing:
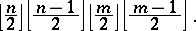 | (a1) |
K. Zarankiewicz [a10] and K. Urbaník [a7] independently claimed and published that 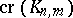 was actually equal to (a1), their argument was reprinted in a book, cited, and used in follow-up papers. However, P. Kainen and G. Ringel discovered a flaw in the argument and the flaw has withstood all attempts for correction (up till 2000). R. Guy deserves much credit for rectifying this confused state of art, see [a2] and [a3].
was actually equal to (a1), their argument was reprinted in a book, cited, and used in follow-up papers. However, P. Kainen and G. Ringel discovered a flaw in the argument and the flaw has withstood all attempts for correction (up till 2000). R. Guy deserves much credit for rectifying this confused state of art, see [a2] and [a3].
D.J. Kleitman showed that (a1) holds for 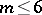 [a4] and also proved that the smallest counterexample to the Zarankiewicz conjecture must occur for odd
[a4] and also proved that the smallest counterexample to the Zarankiewicz conjecture must occur for odd  and
and 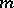 . D.R. Woodall [a9] used an elaborate computer search to show that (a1) holds for
. D.R. Woodall [a9] used an elaborate computer search to show that (a1) holds for 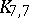 and
and 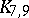 . Thus, the smallest unsettled instances of Zarankiewicz's conjecture are
. Thus, the smallest unsettled instances of Zarankiewicz's conjecture are 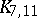 and
and 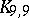 . It is known that
. It is known that
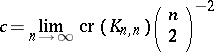 |
exists; however, the value of the limit is not known (as of 2000) [a5]. Woodall's result for 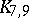 implies
implies 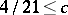 by a standard counting argument, while
by a standard counting argument, while 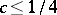 follows from the drawing shown. If (a1) always holds, then
follows from the drawing shown. If (a1) always holds, then 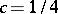 .
.
References
| [a1] | J. Pach, G. Tóth, "Which crossing number is it anyway?" , Proc. 39th Ann. Symp. Foundation of Computer Sci. , IEEE Press (1998) pp. 617–626 |
| [a2] | R.K. Guy, "The decline and fall of Zarankiewicz's theorem" F. Harary (ed.) , Proof Techniques in Graph Theory , Acad. Press (1969) pp. 63–69 |
| [a3] | R.K. Guy, "# 21749" Math. Rev. , 58 (1974) |
| [a4] | D.J. Kleitman, "The crossing number of 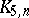 " J. Combin. Th. , 9 (1970) pp. 315–323 " J. Combin. Th. , 9 (1970) pp. 315–323 |
| [a5] | R.B. Richter, C. Thomassen, "Relations between crossing numbers of complete and complete bipartite graphs" Amer. Math. Monthly , 104 (1997) pp. 131–137 |
| [a6] | P. Turán, "A note of welcome" J. Graph Th. , 1 (1977) pp. 7–9 |
| [a7] | K. Urbaník, "Solution du problème posé par P. Turán" Colloq. Math. , 3 (1955) pp. 200–201 |
| [a8] | A.T. White, L.W. Beineke, "Topological graph theory" L.W. Beineke (ed.) R.J. Wilson (ed.) , Selected Topics in Graph Theory , Acad. Press (1978) pp. 15–50 |
| [a9] | D.R. Woodall, "Cyclic-order graphs and Zarankiewicz's crossing-number conjecture" J. Graph Th. , 17 (1993) pp. 657–671 |
| [a10] | K. Zarankiewicz, "On a problem of P. Turán concerning graphs" Fundam. Math. , 41 (1954) pp. 137–145 |
Zarankiewicz crossing number conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zarankiewicz_crossing_number_conjecture&oldid=18710