Young criterion
From Encyclopedia of Mathematics
One of the sufficiency criteria for the convergence of a Fourier series at a point. Let a function 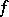 have period
have period 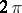 , be Lebesgue integrable over the interval
, be Lebesgue integrable over the interval 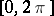 and, on putting
and, on putting  , let it satisfy at the point
, let it satisfy at the point 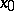 the conditions: 1)
the conditions: 1) 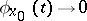 as
as 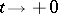 ; 2) the function
; 2) the function 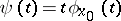 is of finite variation
is of finite variation 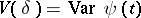 on the interval
on the interval 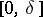 ,
, 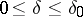 , where
, where 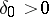 is some fixed number; and 3)
is some fixed number; and 3)  as
as 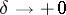 . Then the Fourier series of
. Then the Fourier series of 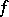 at
at 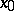 converges to
converges to 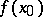 (cf. [2]). Young's criterion is stronger than the Jordan criterion. It was established by W.H. Young [1].
(cf. [2]). Young's criterion is stronger than the Jordan criterion. It was established by W.H. Young [1].
References
| [1] | W.H. Young, "On the convergence of the derived series of Fourier series" Proc. London Math. Soc. , 17 (1916) pp. 195–236 |
| [2] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
Comments
References
| [a1] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
How to Cite This Entry:
Young criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_criterion&oldid=19222
Young criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_criterion&oldid=19222
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article