Wreath product
The wreath product of two groups $A$ and $B$ is constructed in the following way. Let $A^B$ be the set of all functions defined on $B$ with values in $A$. With respect to pointwise multiplication, this set is a group which is the complete direct product of $|B|$ copies of $A$ ($|B|$ denotes the cardinality of $B$); $B$ acts on $A^B$ as a group of automorphisms in the following way: if $b \in B$, $\phi \in A^B$, then $\phi^b(x) = \phi(xb^{-1})$ for $x \in B$. With respect to this operation, one can form the semi-direct product $W$ of $B$ and $A^B$, that is, the set of all pairs $(b,\phi)$, where $b \in B$, $\phi \in A^B$, with multiplication operation given by $$ (b,\phi) (c,\psi) = (bc, \phi^c \psi) \ . $$
The resulting group $W$ is called the Cartesian (or complete) wreath product of $A$ and $B$, and is denoted by $A \mathop{Wr} B$ (or $A \bar{\wr} B$, a denotation of Ph. Hall). If instead of $A^B$ one takes the smaller group $A^{(B)}$ consisting of all functions with finite support, that is, functions taking only non-identity values on a finite set of points, then one obtains a subgroup of $W$ called the wreath product (direct wreath product, discrete wreath product) of $A$ and $B$; it is denoted by $A \mathop{wr} B$ (or $A \wr B$). Both wreath products are widely used for constructing various examples of groups.
References
| [1] | H. Neumann, "Varieties of groups" , Springer (1967) |
| [2a] | M. Krasner, L. Kaloujnine, "Produit complet des groupes de permutations et problème d'extension de groupes I" Acta Sci. Math. Szeged , 13 (1950) pp. 208–230 |
| [2b] | M. Krasner, L. Kaloujnine, "Produit complet des groupes de permutations et problème d'extension de groupes II" Acta Sci. Math. Szeged , 14 (1951) pp. 39–66; 69–82 |
Comments
More generally, let 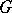 be a group and
be a group and 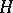 a permutation group, i.e. a group
a permutation group, i.e. a group  acting on a set
acting on a set 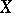 (not transitively or faithfully). Consider the set all pairs
(not transitively or faithfully). Consider the set all pairs
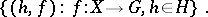 |
A product on this set is defined by
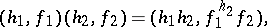 |
where 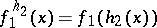 (and
(and 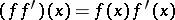 ). This defines a group structure and the resulting group is denoted
). This defines a group structure and the resulting group is denoted  and is called the (complete) wreath product of
and is called the (complete) wreath product of 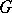 with
with 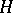 . If
. If 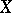 is infinite, then by taking only mappings
is infinite, then by taking only mappings 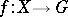 such that
such that 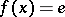 , the unit element in
, the unit element in 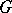 , for almost-all
, for almost-all  one obtains the (restricted) wreath product.
one obtains the (restricted) wreath product.
In the special case where 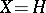 with
with 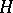 acting on itself by the right regular permutation representation
acting on itself by the right regular permutation representation 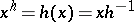 , one obtains the wreath products described above. These are often called the standard wreath product or the regular wreath product.
, one obtains the wreath products described above. These are often called the standard wreath product or the regular wreath product.
If 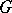 is also a permutation group acting on a set
is also a permutation group acting on a set 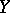 , then
, then 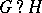 can be seen as a permutation group acting on the set
can be seen as a permutation group acting on the set 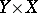 with
with 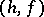 acting as
acting as
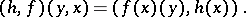 |
Many natural subgroups of the symmetric groups, such as centralizers of elements, normalizers of certain subgroups, Sylow subgroups, are direct products of wreath products. For instance, the normalizer of the Young subgroup, 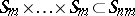 is the wreath product
is the wreath product 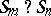 . The wreath product
. The wreath product 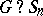 for
for 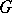 an arbitrary group has been called the complete monomial group of degree
an arbitrary group has been called the complete monomial group of degree  of
of 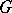 , or the symmetry of degree
, or the symmetry of degree  of
of 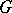 . The wreath products
. The wreath products 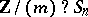 and
and 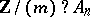 are sometimes termed generalized symmetric groups and generalized alternating groups;
are sometimes termed generalized symmetric groups and generalized alternating groups; 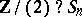 is a hyper-octahedral group.
is a hyper-octahedral group.
A more general standard product is the twisted wreath product, which incorporates an action of a subgroup 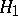 of
of 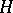 on
on 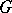 , cf. [a4].
, cf. [a4].
References
| [a1] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) pp. §15 |
| [a2] | M. Hall jr., "The theory of groups" , Macmillan (1959) pp. 81ff |
| [a3] | A. Kerber, "Representations of permutation groups" , I-II , Springer (1971–1975) |
| [a4] | M. Suzuki, "Group theory" , 1 , Springer (1982) |
The wreath product of semi-groups is a construction assigning to two semi-groups a third in the following way: The wreath product 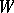 of
of 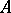 and
and 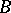 has as underlying set
has as underlying set 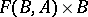 , where
, where 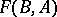 is the semi-group of all mappings from
is the semi-group of all mappings from 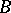 into
into 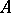 under pointwise multiplication, and the operation on
under pointwise multiplication, and the operation on 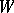 is given by the formula:
is given by the formula: 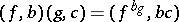 , where the mapping
, where the mapping  is defined by
is defined by 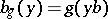 . The wreath product of
. The wreath product of 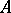 and
and 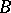 is written as
is written as 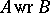 . This is the standard wreath product; for other definitions and generalizations of the wreath product see [1], [2], [4]–[7].
. This is the standard wreath product; for other definitions and generalizations of the wreath product see [1], [2], [4]–[7].
The wreath product of 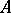 and
and 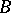 contains the direct product
contains the direct product 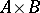 as a sub-semi-group. If
as a sub-semi-group. If 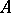 has an identity, then any ideal extension of
has an identity, then any ideal extension of 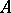 by
by 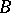 can be imbedded in
can be imbedded in 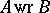 (see [3]).
(see [3]).
The question of when 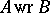 inherits various properties of
inherits various properties of 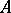 and
and  has been investigated mainly for various types of simplicity (see Simple semi-group). Some examples follow. If
has been investigated mainly for various types of simplicity (see Simple semi-group). Some examples follow. If 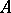 and
and  are ideally-simple semi-groups and
are ideally-simple semi-groups and 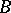 is a semi-group with right cancellation, then
is a semi-group with right cancellation, then 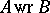 is an ideally-simple semi-group. If
is an ideally-simple semi-group. If 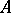 and
and 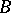 are completely-simple semi-groups and
are completely-simple semi-groups and 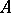 is left-simple, then
is left-simple, then 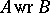 is completely simple [3]. If
is completely simple [3]. If 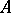 and
and  are semi-groups with completely-simple kernels (see Kernel of a semi-group), then
are semi-groups with completely-simple kernels (see Kernel of a semi-group), then 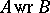 has a completely-simple kernel [4], and, moreover, the kernel of
has a completely-simple kernel [4], and, moreover, the kernel of 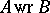 is equal to the square of the wreath product of the kernels [7]. If one of
is equal to the square of the wreath product of the kernels [7]. If one of 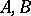 is regular and the other is left-simple, then
is regular and the other is left-simple, then 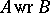 is regular [6]. Let
is regular [6]. Let 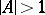 ; then
; then 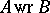 is an inverse semi-group (cf. Inversion semi-group) (or right group) if and only if
is an inverse semi-group (cf. Inversion semi-group) (or right group) if and only if 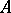 is an inverse semi-group (or right group, respectively) and
is an inverse semi-group (or right group, respectively) and 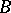 is a group [6].
is a group [6].
Wreath products can be used to give a compact proof of Evan's theorem that every countable semi-group 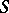 can be imbedded in a semi-group with two generators [1], and in the case when
can be imbedded in a semi-group with two generators [1], and in the case when 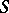 is finitely generated and periodic it can be imbedded in a periodic semi-group with two generators.
is finitely generated and periodic it can be imbedded in a periodic semi-group with two generators.
The wreath product and its generalizations play an important role in the algebraic theory of automata. For example, they can be used to prove the theorem on the decomposition of every finite semi-group automaton into a step-by-step combination of flip-flops and simple group automata ([2], see also [5]), the so-called Krohn–Rhodes theorem.
References
| [1] | B.H. Neumann, "Embedding theorems for semigroups" J. London Math. Soc. , 35 : 138 (1960) pp. 184–192 |
| [2] | K. Krohn, J. Rhodes, "Algebraic theory of machines. I Prime decomposition theorem for finite semigroups and machines" Trans. Amer. Math. Soc. , 116 (1965) pp. 450–464 |
| [3] | R.P. Hunter, "Some results on wreath products of semigroups" Bull. Soc. Math. Belgique , 18 : 1 (1966) pp. 3–16 |
| [4] | J.D., jr. McKnight, E. Sadowski, "The kernel of the wreath product of semigroups" Semigroup Forum , 4 (1972) pp. 232–236 |
| [5] | M.A. Arbib (ed.) , Algebraic theory of machines, languages and semigroups , Acad. Press (1968) |
| [6] | Yu.G. Koshelev, "Wreath products and equations in semigroups" Semigroup Forum , 11 : 1 (1975) pp. 1–13 (In Russian) ((English abstract.)) |
| [7] | S. Nakajima, "On the kernel of the wreath product of completely simple semigroups II" , Proc. First Symp. Semigroups (Shimane Univ. Matsue, 1977) , Shimane Univ. Matsue (1977) pp. 84–88 |
E.A. GolubovL.N. Shevrin
Wreath product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wreath_product&oldid=35297