Witt vector
An element of an algebraic construct, first proposed by E. Witt [1] in 1936 in the context of the description of unramified extensions of $p$-adic number fields. Witt vectors were subsequently utilized in the study of algebraic varieties over a field of positive characteristic [3], in the theory of commutative algebraic groups [4], [5], and in the theory of formal groups [6]. Let $A$ be an associative, commutative ring with unit element. Witt vectors with components in $A$ are infinite sequences $a = (a_0,a_1,\ldots)$, $a_i \in A$, which are added and multiplied in accordance with the following rules: $$ (a_0,a_1,\ldots) \oplus (b_0,b_1,\ldots) = (S_0(a_0;b_0), S_1(a_0,a_1;b_0,b_1), \ldots) $$ $$ (a_0,a_1,\ldots) \otimes (b_0,b_1,\ldots) = (M_0(a_0;b_0), M_1(a_0,a_1;b_0,b_1), \ldots) $$
where $S_n,M_n$ are polynomials in the variables $X_0,\ldots,X_n$, $Y_0,\ldots,Y_n$ with integer coefficients, uniquely defined by the conditions $$ \Phi_n(S_0,\ldots,S_n) = \Phi_n(X_0,\ldots,X_n) + \Phi_n(Y_0,\ldots,Y_n) $$ $$ \Phi_n(M_0,\ldots,M_n) = \Phi_n(X_0,\ldots,X_n) \cdot \Phi_n(Y_0,\ldots,Y_n) $$ where $$ \Phi_n(Z_0,\ldots,Z_n) = Z_0^{p^n} + p Z_1^{p^{n-1}} + \cdots + p^n Z^n $$ are polynomials, $n \in \mathbf{N}$ and $p$ is a prime number. In particular, $$ S_0 = X_0 + Y_0 \ ;\ \ \ S_1 = X_1 + Y_1 - \sum_{i=1}^{p-1} \frac{1}{p} \binom{p}{i} X_0^i Y_0^{p-i} $$ $$ M_0 = X_0 \cdot Y_0 \ ;\ \ \ M_1 = X_0^p Y_1 + X_1 Y_0^p + p X_1 Y_1 \ . $$
The Witt vectors with the operations introduced above form a ring, called the ring of Witt vectors and denoted by $W(A)$. For any natural number $n$ there also exists a definition of the ring $W_n(A)$ of truncated Witt vectors of length $n$. The elements of this ring are finite tuples $a = (a_0,\ldots,a_{n-1})$, $a_i \in A$ with the addition and multiplication operations described above. The canonical mappings $$ R : W_{n+1}(A) \rightarrow W_n(A) $$ $$ R : (a_0,\ldots,a_n) \mapsto (a_0,\ldots,a_{n-1}) $$ $$ T : W_n(A) \rightarrow W_{n+1}(A) $$ $$ T : (a_0,\ldots,a_{n-1}) \mapsto (0,a_0,\ldots,a_{n-1}) $$ are homomorphisms. The rule $A \to W(A)$ (or $A \to W_n(A)$) defines a covariant functor from the category of commutative rings with unit element into the category of rings. This functor may be represented by the ring of polynomials $\mathbf{Z}[X_0,X_1,\ldots]$ (or $\mathbf{Z}[X_0,X_1,\ldots,X_n]$) on which the structure of a ring object has been defined. The spectrum $\mathrm{Spec}\mathbf{Z}[X_0,X_1,\ldots]$ (or $\mathrm{Spec}\mathbf{Z}[X_0,X_1,\ldots,X_n]$) is known as a Witt scheme (or a truncated Witt scheme) and is a ring scheme [3].
Each element $a \in A$ defines a Witt vector $$ a^T = (a,0,0,\ldots) \in W(A) $$ called the Teichmüller representative of the element $a$. If $A = k$ is a perfect field of characteristic $p>0$, then $W(k)$ is a complete discrete valuation ring of zero characteristic with field of residues $k$ and maximal ideal $pW(k)$. Each element $w \in W(k)$ can be uniquely represented as $$ w = w_0^T + pw_1^T + p^2 w_2^T + \cdots $$ where $w_i \in k$. Conversely, each such ring $A$ with field of residues $k = A/(p)$ is canonically isomorphic to the ring $W(k)$. The Teichmüller representation makes it possible to construct a canonical multiplicative homomorphism $k \to W(k)$, splitting the mapping $W(k) \to W(k)/(p)$.
If $k = \mathbf{F}_p$ is the prime field of $p$ elements, $W(k)$ is the ring of integral $p$-adic numbers $\mathbf{Z}_p$.
References
| [1] | E. Witt, "Zyklische Körper und Algebren der characteristik $p$ vom Grad $p^n$. Struktur diskret bewerteter perfekter Körper mit vollkommenem Restklassen-körper der Charakteristik $p$" J. Reine Angew. Math. , 176 (1936) pp. 126–140 Zbl 0016.05101 |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [3] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
| [4] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) MR0103191 |
| [5] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1971) MR1611211 MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 Zbl 0134.16503 |
| [6] | J. Dieudonné, "Groupes de Lie et hyperalgèbres de Lie sur un corps de charactéristique $p$ VII" Math. Ann. , 134 (1957) pp. 114–133 DOI 10.1007/BF01342790 Zbl 0086.02605 |
Comments
There is a generalization of the construction above which works for all primes $p$ simultaneously, [a3]: a functor $W : \mathsf{Ring} \to \mathsf{Ring}$ called the big Witt vector. Here, $\mathsf{Ring}$ is the category of commutative, associative rings with unit element. The functor described above, of Witt vectors of infinite length associated to the prime $p$, is a quotient of $W$ which can be conveniently denoted by $W_{p^\infty}$.
For each $n \in \{1,2,\ldots\}$, let $w_n(X)$ be the polynomial $$ w_n(X) = \sum_{d | n} d X^{n/d} \ . $$
Then there is the following characterization theorem for the Witt vectors. There is a unique functor $W : \mathsf{Ring} \to \mathsf{Ring}$satisfying the following properties: 1) as a functor $W : \mathsf{Ring} \to \mathsf{Set}$, $W(A) = \{(a_1,a_2,\ldots) : a_i \in A\}$ and $W(\phi)((a_1,a_2,\ldots)) = (\phi(a_1),\phi(a_2),\ldots)$ for any ring homomorphism $\phi : A \to B$; 2) $w_{n,A} : W(A) \to A$, $w_{n,A} : (a_1,a_2,\ldots) \mapsto w_n(a_1,a_2,\ldots)$ is a functorial homomorphism of rings for every $n$ and $A$.
The functor $W$ admits functorial ring endomorphisms $\mathbf{f}_n : W \to W$, for every $n \in \{1,2,\ldots\}$, that are uniquely characterized by $wn \mathbf{f}_m = w_{nm}$ for all $m,n \in \{1,2,\ldots\}$. Finally, there is a functorial homomorphism $\Delta : W({-}) \to W(W({-}))$ that is uniquely characterized by the property $w_{n,W(A)} \Delta_A = \mathbf{f}_{n,A}$ for all $n$,$A$.
To construct $W(A)$, define polynomials $\Sigma_n$; $\Pi_n$; $r_n$ for $n \in \{1,2,\ldots\}$ by the requirements $$ w_n(\Sigma_1,\ldots,\Sigma_n) = w_n(X) + w_n(Y) \ ; $$ $$ w_n(\Pi_1,\ldots,\Pi_n) = w_n(X) \cdot w_n(Y) \ ; $$ $$ w_n(r1,\ldots,r_n) = - w_n(X) \ . $$
The $\Sigma_n$ and $\Pi_n$ are polynomials in $X_1,\ldots,X_n$; $Y_1,\ldots,Y_n$ and the $r_n$ are polynomials in the $X_1,\ldots,X_n$ and they all have integer coefficients. Now $W(A)$ is defined as the set $W(A) = \{ a = (a_1,a_2,\ldots) : a_i \in A \}$ with operations : $$ (a_1,a_2,\ldots) + (b_1,b_2,\ldots) = (\Sigma_1(a,b), \Sigma_2(a,b), \ldots) \ ; $$ $$ (a_1,a_2,\ldots) \cdot (b_1,b_2,\ldots) = (\Pi_1(a,b), \Pi_2(a,b), \ldots) \ ; $$ $$ - (a_1,a_2,\ldots) = (r_1(a), r_2(a), \ldots) \ . $$
The zero of $W(A)$ is $(0,0,0,\ldots)$ and the unit element is $(1,0,0,\ldots)$. The Frobenius endomorphisms $\mathbf{f}_n$ and the Artin–Hasse exponential $\Delta$ are constructed by means of similar considerations, i.e. they are also given by certain universal polynomials. In addition there are the Verschiebung morphisms $\mathbf{V}_n : W({-}) \to W({-})$, which are characterized by $$ w_n \mathbf{V}_m = \begin{cases} 0 & \text{if}\, n \not\mid m \\ n w_{m/n} & \text{if}\, n \mid m \end{cases} \ . $$
The $\mathbf{V}_n$ are group endomorphisms of $W(A)$ but not ring endomorphisms.
The ideals $I_n = \{(0,\ldots,0,a_{n+1},a_{n+2},\ldots)\}$ define a topology on $W(A)$ making it a separated complete topological ring.
For each $A \in \mathsf{Ring}$, let $\Lambda(A)$ be the Abelian group $1 + t A[[t]]$ under multiplication of power series; $$ \bar E : W(A) \rightarrow \Lambda(A) $$ $$ \bar E : (a_1,a_2,\ldots) \mapsto \prod_{i=1}^\infty \left({ 1 - a_i t^i }\right) $$ defines a functional isomorphism of Abelian groups, and using the isomorphism $\bar E$ there is a commutative ring structure on $\Lambda(A)$. Using $\bar E$ the Artin–Hasse exponential $\Delta$ defines a functorial homomorphism of rings $W(A) \to \Lambda(W(A))$ making $W(A)$ a functorial special $\lambda$-ring. The Artin–Hasse exponential $\Delta : W \mapsto W \circ W$ defines a cotriple structure on $W$ and the co-algebras for this co-triple are precisely the special $\lambda$-rings (cf. also Category and Triple).
On $\Lambda(A)$ the Frobenius and Verschiebung endomorphisms satisfy $$ \mathbf{f}_n (1 - at) = 1 - a^n t $$ $$ V_n(f(t)) = f(t^n) $$ and are completely determined by this (plus functoriality and additivity in the case of $\mathbf{f}_n$).
For each supernatural number $\mathbf{n} = (\alpha_p) : \alpha_p \in \{0,1,2,\ldots\} \cup \{\infty\}$, $p$ prime , one defines $N(\mathbf{n}) = \{ n \in \{1,2,\ldots\} : \nu_p(n) \le \alpha_p \}$, where $\nu_p(n)$ is the $p$-adic valuation of $n$, i.e. the number of prime factors $p$ in $n$. Let $$ \mathfrak{a}_{\mathbf{n}}(A) = \{ (a_1,a_2,\ldots) : a_i \in A \,,\, a_d = 0 \,\text{for all}\, d \in N(\mathbf{n}) \} \ . $$
Then $\mathfrak{a}_{\mathbf{n}}(A) $ is an ideal in $W(A)$ and for each supernatural $\mathbf{n}$ a corresponding ring of Witt vectors is defined by $$ W_{\mathbf{n}}(A) = W(A) / \mathfrak{a}_{\mathbf{n}}(A) \ . $$
In particular, one thus finds $W_{p^\infty}$, the ring of infinite-length Witt vectors for the prime $p$, discussed in the main article above, as a quotient of the ring of big Witt vectors $W(A)$.
The Artin–Hasse exponential $\Delta : W \to W \circ W$ is compatible in a certain sense with the formation of these quotients, and using also the isomorphism $\bar E$ one thus finds a mapping $$ \mathbf{Z}_p = W_{p^\infty}(\mathbf{F}_p) \to \Lambda(W_{p^\infty}(\mathbf{F}_p)) = \Lambda(\mathbf{Z}_p) $$ where $\mathbf{Z}_p$ denotes the $p$-adic integers and $\mathbf{F}_p$ the field of $p$ elements, which can be identified with the classical morphism defined by Artin and Hasse [a1], [a2], [a3].
As an Abelian group 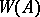 is isomorphic to the group of curves
is isomorphic to the group of curves 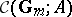 of curves in the one-dimensional multiplicative formal group
of curves in the one-dimensional multiplicative formal group 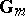 . In this way there is a Witt-vector-like Abelian-group-valued functor associated to every one-dimensional formal group. For special cases, such as the Lubin–Tate formal groups, this gives rise to ring-valued functors called ramified Witt vectors, [a3], [a4].
. In this way there is a Witt-vector-like Abelian-group-valued functor associated to every one-dimensional formal group. For special cases, such as the Lubin–Tate formal groups, this gives rise to ring-valued functors called ramified Witt vectors, [a3], [a4].
Let 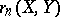 be the sequence of polynomials with coefficients in
be the sequence of polynomials with coefficients in 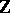 defined by
defined by
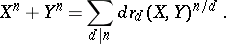 |
The Cartier ring 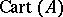 is the ring of all formal expressions
is the ring of all formal expressions
 | (*) |
with the calculation rules
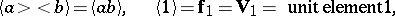 |
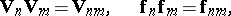 |
 |
 |
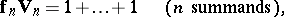 |
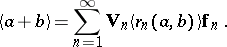 |
Commutative formal groups over  are classified by certain modules over
are classified by certain modules over 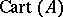 . In case
. In case 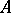 is a
is a 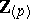 -algebra, a simpler ring
-algebra, a simpler ring 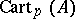 can be used for this purpose. It consists of all expressions (*) where now the
can be used for this purpose. It consists of all expressions (*) where now the 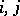 only run over the powers
only run over the powers 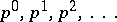 of the prime
of the prime 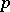 . The calculation rules are the analogous ones. In case
. The calculation rules are the analogous ones. In case 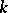 is a perfect field of characteristic
is a perfect field of characteristic 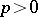 and
and 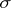 denotes the Frobenius endomorphism of
denotes the Frobenius endomorphism of 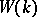 (which in this case is given by
(which in this case is given by 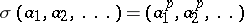 ), then
), then 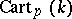 can be described as the ring of all expressions
can be described as the ring of all expressions
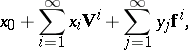 |
in two symbols  and
and 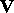 and with coefficients in
and with coefficients in 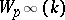 , with the extra condition
, with the extra condition 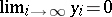 and the calculation rules
and the calculation rules
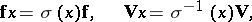 |
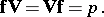 |
This ring, and also its subring of all expressions
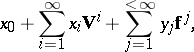 |
is known as the Dieudonné ring  and certain modules (called Dieudonné modules) over it classify unipotent commutative affine group schemes over
and certain modules (called Dieudonné modules) over it classify unipotent commutative affine group schemes over 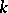 , cf. [a5].
, cf. [a5].
References
| [a1] | E. Artin, H. Hasse, "Die beide Ergänzungssätze zum Reciprozitätsgesetz der $\ell$-ten Potenzreste im Körper der $\ell$-ten Einheitswurzeln" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 146–162 |
| [a2] | G. Whaples, "Generalized local class field theory III: Second form of the existence theorem, structure of analytic groups" Duke Math. J. , 21 (1954) pp. 575–581 MR73645 |
| [a3] | M. Hazewinkel, "Twisted Lubin–Tate formal group laws, ramified Witt vectors and (ramified) Artin–Hasse exponentials" Trans. Amer. Math. Soc. , 259 (1980) pp. 47–63 MR0561822 Zbl 0437.13014 |
| [a4] | M. Hazewinkel, "Formal group laws and applications" , Acad. Press (1978) MR506881 |
| [a5] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1971) MR1611211 MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 Zbl 0134.16503 |
Witt vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_vector&oldid=37687