Wilson theorem
From Encyclopedia of Mathematics
Let 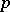 be a prime number. Then the number
be a prime number. Then the number 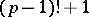 is divisible by
is divisible by 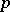 . The theorem was first formulated by E. Waring (1770) and is, according to him, due to J. Wilson. It was proved by J.L. Lagrange in 1771. A primality test for integers follows from Wilson's theorem: A natural number
. The theorem was first formulated by E. Waring (1770) and is, according to him, due to J. Wilson. It was proved by J.L. Lagrange in 1771. A primality test for integers follows from Wilson's theorem: A natural number  will be prime if and only if
will be prime if and only if
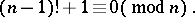 |
This test is not recommended for practical use, since the factorial involved rapidly becomes very large.
References
| [1] | A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian) |
| [2] | E. Trost, "Primzahlen" , Birkhäuser (1953) |
| [3] | I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian) |
Comments
In fact, also the converse is true (and usually also called Wilson's theorem): Let 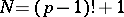 , with
, with 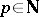 . Then
. Then  is divisible by
is divisible by 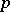 if and only if
if and only if 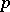 is a prime number.
is a prime number.
References
| [a1] | D. Shanks, "Solved and unsolved problems in number theory" , Chelsea, reprint (1978) |
| [a2] | M.R. Schroeder, "Number theory in science and communication" , Springer (1984) pp. 103 |
| [a3] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1960) pp. 68 |
How to Cite This Entry:
Wilson theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wilson_theorem&oldid=17357
Wilson theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wilson_theorem&oldid=17357
This article was adapted from an original article by N.I. Klimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article