Weyl module
Objects that are of fundamental importance for the representation theory of reductive algebraic groups $G$ (cf. Representation of a group; Reductive group; Algebraic group). Considering such groups as group schemes (cf. Group scheme), that is, as a family of groups $G ( K )$, where $K$ varies over some class of commutative rings, Weyl modules are universally defined and possess a standard basis which is independent of the choice of $K$. Moreover, for algebraically closed fields $K$ of characteristic $0$ they constitute a complete set of non-isomorphic irreducible rational representations of $G ( K )$. This makes possible a "modular theory" for the rational representations of these groups analogous to Brauer's modular representation theory of finite groups (cf. also Finite group, representation of a). However, whereas for finite groups the reduction modulo a prime $p$ happens with respect to the field of coefficients of the representations, in the case of an algebraic group this reduction is carried out with respect to the field of definition of the group.
Below, the example of general linear groups will be discussed in more detail to illuminate this reduction process. For these, R. Carter and G. Lusztig used the term "Weyl module" the first time in their fundamental paper [a5], where they discussed polynomial representations of general linear groups and indicated how their methods generalize to arbitrary reductive groups. There these modules were constructed in the "same" way as in [a17].
General linear groups.
Let $n \in \mathbf N$ and let $G = \operatorname{GL} _ { n } ( K )$ for some field $K$ (cf. General linear group). Let $E = K ^ { n }$ be the natural module of $G$. For a non-negative integer $r$, the group $G$ acts on $E ^{ \otimes r}$ diagonally, and this action centralizes the natural place permutation action of the symmetric group $\mathfrak{S}_r$ on $E ^{ \otimes r}$. The image of $K G$ in $\operatorname{End}_{K}( E ^ { \otimes r } )$ is the Schur algebra $S ( n , 1 )$. This is a finite-dimensional quasi-hereditary $K$-algebra and the indecomposable representations of $S ( n , r )$ for $0 \leq r \in \bf Z$ are precisely the indecomposable polynomial representations of $G$. For fields $K$ of characteristic $0$, the polynomial representations of $G$ has been investigated by I. Schur in his famous dissertation [a12]. He rederived all these results in a paper [a13] of 1927 in terms of the module $E ^{ \otimes r}$. Among other things, he showed that $E ^{ \otimes r}$ is a completely reducible $G$-module, indeed the category of polynomial representations of $G$ is semi-simple. Weyl modules are defined to be the irreducible constituents of the tensor space $E ^{ \otimes r}$, where $r$ runs through $\mathbf{N} \cup \{ 0 \}$. However, Weyl modules are defined for arbitrary characteristic $p \geq 0$ of the field $K$. Those occurring for $p = 0$ as irreducible constituents of the tensor space $E ^{ \otimes r}$ are parametrized by partitions $\lambda$ of $r$ into $n$ parts. Thus, $\lambda = ( \lambda _ { 1 } , \ldots , \lambda _ { n } )$ is a decreasing sequence of non-negative integers whose sum is $r$. If the requirement "decreasing" in the definition above is dropped, $\lambda$ is called a composition of $r$ into $n$ parts. The union of the sets $\Lambda ( n , r )$ of compositions of $r$ into $n$ parts, where $0 \leq r \in \bf Z$, is the set of weights of $G$. The partitions in $\Lambda ( n , r )$ are also called dominant weights and are denoted by $\Lambda ^ { + } ( n , r )$. One depicts the composition $\lambda$ into $n$ parts by its associated Young diagram consisting of crosses in the plane in $n$ rows, where the $i$th row contains $\lambda _ { i }$ crosses without gap and the first crosses in the rows are the crosses in the first column. This Young diagram is usually denoted by $[ \lambda ]$.
Let $\lambda$ be a composition of $r$. A $\lambda$-tableau $t$ is a Young diagram of shape $\lambda$, where the crosses are replaced by the numbers $1 , \ldots , r$ in some order (cf. also Young tableau). The $\lambda$-tableau where these numbers are inserted in order along the rows downward, is called the initial $\lambda$-tableau and is denoted by $t ^ { \lambda }$.
A $\lambda$-tableau is row standard if the numbers increase along the rows and column standard if the increase occurs down the columns. A row-and-column standard tableau is called standard. Obviously, the initial tableau is always standard. The symmetric group $\mathfrak{S}_r$ acts on the set of $\lambda$-tableaux, where $\lambda$ is a composition of $r$. If $t$ is a $\lambda$-tableau, the set $R ( t )$ of elements of $\mathfrak{S}_r$ permuting the entries in each row is a subgroup of $\mathfrak{S}_r$, the row stabilizer of $t$. Similarly one defines the column stabilizer $C ( t )$ of $t$. In particular, for $\lambda = ( \lambda _ { 1 } , \ldots , \lambda _ { n } ) \in \Lambda ( n , r )$ the row stabilizer $R ( t ^ { \lambda } )$ of the initial $\lambda$-tableau is the standard Young subgroup $Y _ { \lambda }$ of $\mathfrak{S}_r$, which is the symmetric group
\begin{equation*} \mathfrak { S } _ { \{ 1 , \ldots , \lambda _ { 1 } \} } \times \mathfrak { S } _ { \{ \lambda _ { 1 } + 1 , \ldots , \lambda _ { 1 } + \lambda _ { 2 } \} } \times \dots \end{equation*}
\begin{equation*} \ldots \times \mathfrak { S } _ { \{ \lambda _ { 1 } + \ldots + \lambda _ { n - 1 } + 1 , \ldots , r \} }, \end{equation*}
considered as a subgroup of $\mathfrak{S}_r$ in the natural way.
It is now possible to define Weyl modules for $ \operatorname {GL} _ { n } ( K )$ for arbitrary fields $K$: For $\lambda = ( \lambda _ { 1 } , \ldots , \lambda _ { n } ) \in \Lambda ( n , r )$ one defines the element $e_{ \lambda}$ of the tensor space $E ^{ \otimes r}$ to be
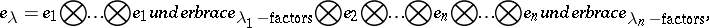 |
the element $y \lambda $ of the group algebra $K \mathfrak { S } _ { r }$ to be the alternating sum
\begin{equation*} y _ { \lambda } = \sum _ { \pi \in C ( t ) } \operatorname { sg } ( \pi ) \pi , \end{equation*}
where $\operatorname{sg} ( \pi )$ denotes the sign of $\pi$, and finally
\begin{equation*} z _ { \lambda } = e _ { \lambda } y _ { \lambda } \in E^{ \bigotimes r }. \end{equation*}
For $\lambda \in \Lambda ^ { + } ( n , r )$, the Weyl module to the highest weight $\lambda$ is the left $G$-submodule of the tensor space $E ^{ \otimes r}$ generated by $z_ \lambda$ and is denoted by $\Delta ( \lambda )$. Thus,
\begin{equation*} \Delta ( \lambda ) = K \operatorname{GL} _ { n } ( K ) z _ { \lambda }, \end{equation*}
provided $K$ is infinite.
The vector $z_ \lambda$ is an eigenvector of the torus $T$ of diagonal matrices in $G$. The eigenvalue is a linear character of $T$ given as
\begin{equation*} \operatorname { diag } ( t _ { 1 } , \ldots , t _ { n } ) \mapsto t _ { 1 } ^ { \lambda _ { 1 } } \ldots t _ { n } ^ { \lambda _ { n } } \in K, \end{equation*}
which again is denoted by $\lambda$ (cf. also Character of a group). Thus, the weights $\Lambda ( n )$ of $ \operatorname {GL} _ { n } ( K )$ are in bijection with the linear characters of $T$. The module $\Delta ( \lambda )$ decomposes into direct sum of eigenspaces of the action of $T$, called weight spaces and for $\lambda \in \Lambda ^ { + } ( n , r )$ all occurring weights belong to $\Lambda ( n , r )$. Let $\Delta ( \lambda ) ^ { \mu }$ denote the eigenspace of $\Delta ( \lambda )$ to weight $\mu$, and define the formal character of $\Delta ( \lambda )$ to be the formal sum
\begin{equation*} \chi _ { \lambda } = \sum _ { \mu \in \Lambda ( n ) } \operatorname { dim } _ { K } ( \Delta ( \lambda ) ^ { \mu } ) _ { e _ { \mu } }, \end{equation*}
where $e _ { \mu }$ denotes a formal basis element of the integral group ring ${\bf Z} \Lambda ( n )$ corresponding to $\mu$. The formal character $\chi_{ \lambda}$ is known by formulas of H. Weyl, B. Kostant and H. Freudenthal (see also Character formula). This will be explained below in detail, in the more general context of reductive groups. It turns out that $\lambda$ is the highest weight with respect to the lexicographic order on $\Lambda ( n )$ occurring with non-zero multiplicity in $\Delta ( \lambda )$ and it occurs with multiplicity one. Moreover, $\Delta ( \lambda )$ is universal with this property, that is, every polynomial $G$-module which is generated by an eigenvector to weight $\lambda$ such that the corresponding eigenspace is one dimensional and each occurring weight coming later in the lexicographic order is an epimorphic image of $\Delta ( \lambda )$.
It is obvious that no proper submodule of $\Delta ( \lambda )$ can contain the highest weight vector $z_ \lambda$, hence the sum of all proper submodules is the unique maximal submodule of $\Delta ( \lambda )$. The corresponding irreducible factor module is denoted by $L ( \lambda )$. It turns out that the set of all $L ( \lambda )$, where $\lambda$ runs through the set $\Lambda ^ { + } ( n )$ of dominant weights on $G$, is a complete set of non-isomorphic irreducible polynomial $G$-modules. Tensoring by arbitrary negative powers of the one-dimensional polynomial representation of $G$ which takes every matrix to its determinant, one obtains a full classification of all irreducible rational representations of general linear groups.
The space $E ^{ \otimes r}$ admits a bilinear form $\langle \, .\, ,\, . \, \rangle$ which is $G$-invariant and contravariant in the sense that
\begin{equation*} \langle g x , y \rangle = \left\langle x , g ^ { T } y \right\rangle , \quad \forall g \in G, \end{equation*}
where $g ^ { T }$ denotes the transpose of $g$. The space $\Delta ( \lambda ) ^ { \perp }$ orthogonal to the kernel of the natural projection $E ^ { \otimes r } \rightarrow \Delta ( \lambda )$ with respect to this form is again a $G$-module, denoted by $\nabla ( \lambda )$, and has properties dual to those of Weyl modules. So, it has the same formal character and its socle is simple and is isomorphic to $L ( \lambda )$.
There is another interpretation of the $\nabla$-modules, namely as induced modules from linear representations of a Borel subgroup $B$ of $G$: One may take $B$ to be the set of all upper-triangular matrices in $G$. Then every linear representation of $B$ is a linear character $\lambda$ of $T$, considered as a representation of $B$, where the unipotent radical $U$ of $B = T U$ acts trivially. The restriction functor to algebraic subgroups $H$ of an algebraic group $G$ has an right adjoint, given by taking for a rational $H$-module $M$ the set of $H$-equivariant morphisms from $G$ to $M$. It is called induction and is denoted by $\operatorname { Ind } _ { { H } } ^ { G }$. (The restriction functor has also a left adjoint, given by tensoring up representations. But whereas for finite groups the left and right adjoint of the restriction functor are isomorphic, this is not true in the context of algebraic groups; in fact, the tensored module is not even rational, in general.) The $G$-module $\nabla ( \lambda )$ is the induced module $\operatorname {ind} _ { K B } ^ { K G } ( \lambda )$.
For further reference and results on the special case of general linear groups, in particular for explicit formulas for bases of Weyl modules and induced modules in terms of bi-determinants, see the fundamental monograph of J.A. Green [a6].
Reductive groups.
All this generalizes to arbitrary reductive groups. For simplicity it is assumed that $G$ is a simple algebraic group of universal type over some algebraically closed field $K$. The general case can be derived from this one. For example, the special linear groups $\operatorname { SL} _ { n } ( K )$ are of this form. The representations of $ \operatorname {GL} _ { n } ( K )$ can be derived from those of $\operatorname { SL} _ { n } ( K )$ by extending the action of diagonal matrices localizing, and those of $\operatorname { PSL } _ { n } ( K )$ by considering only a certain sublattice of the weight lattice of $\operatorname { SL} _ { n } ( K )$.
Associated with $G$ is again a weight lattice $\Lambda$, which may be considered as a space of linear characters of a maximal torus $T$ of $G$. This is a $\bf Z$-lattice of dimension $n$, the Lie rank of $G$, with basis consisting of the so-called fundamental weights. There is a partial order on $\Lambda$, setting $\lambda \leq \mu$ if $\mu - \lambda$ is a linear combination of the fundamental weights with non-negative coefficients. The linear combinations of the fundamental weights, where all coefficients are non-negative, are called dominant weights. The set of dominant weights is denoted by $\Lambda ^ { + }$. There are several ways to define Weyl modules $\Delta ( \lambda )$ for dominant weights $\lambda$. The two most important ones are briefly described below.
First, one may extend $\lambda$ to a linear representation of a Borel subgroup $B = T U$, where $U$ is the unipotent radical of $B$ and is in the kernel of $\lambda$. Inducing this $B$-module to $G$ produces $\nabla ( \lambda )$. Similar to $ \operatorname {GL} _ { n } ( K )$, the group $G$ admits the notion of a contravariant dual module: Given any rational left module $V$ of $G$, the natural right $G$-module structure on the dual space $V ^ { * } = \operatorname { Hom } _ { K } ( V , K )$ can be turned into a left module structure using any anti-automorphism of $K G$. Usually one considers the mapping induced by taking inverses in $G$. For contravariant duality one uses a certain different anti-automorphism of $G$ (which is given by transposing matrices in the special case of $G = \operatorname{GL} _ { n } ( K )$). The Weyl module $\Delta ( \lambda )$ is then defined to be the contravariant dual module $\nabla ( \lambda ) ^ { * }$. (One can use the ordinary dual as well, but then one has to carry out a shift in the highest weight.) For non-dominant weights $\lambda$ the induced module $\operatorname {Ind} ^{ G }_ { B } ( \lambda )$ is the zero module. Indeed, since $G$ is assumed to be simple of universal type, one can use this property to define dominant weights.
The second approach for setting up Weyl modules involves the complex simple Lie algebra $\frak g$ associated with $G$. So, for example, for $G = \operatorname {SL} _ { n } ( K )$ the associated complex Lie algebra $\frak g$ is the set $\mathfrak{sl}_n ( \mathbf{C} )$ of complex $( n \times n )$-matrices of trace $0$, where the Lie bracket is given, as usually, by commutators. One chooses a maximal Abelian subalgebra $\mathfrak h $ of $\frak g$, e.g. the set of diagonal matrices in the example of $\mathfrak{sl}_n ( \mathbf{C} )$. The adjoint action of $\mathfrak h $ on $\frak g$ determines a root system $\Phi$ with basis $\Sigma$ and, corresponding to the choice of $\Sigma$, a decomposition $\Phi = \Phi ^ { + } \cup \Phi ^ { - }$ into positive and negative roots. There holds the root-space decomposition
\begin{equation*} \mathfrak{g} = \sum _ { \alpha \in \Phi ^ { - } } ^{ \bigoplus} \mathfrak{g} _ { \alpha } \bigoplus \mathfrak{h} \bigoplus \sum_ { \gamma \in \Phi ^ { + } } ^{\bigoplus} \mathfrak{g} _ { \gamma } \end{equation*}
of $\frak g$. Thus, $\Phi$ is a subset of ${\frak h} ^ { * } = \operatorname{Hom} _ {\bf C } ( h , {\bf C} )$ consisting of the non-zero eigenvalues of $\mathfrak h $ on $\frak g$ and $\mathfrak { g } _ { \alpha }$ is the eigenspace to eigenvalue $\alpha \in \Phi$. All these eigenspaces are one-dimensional and there is a special basis $\frak B$, called Chevalley basis, of $\frak g$, which is not only compatible with this decomposition, but also has particularly nice structural constants:
\begin{equation*} \mathfrak { B } = \{ e _ { \pm \alpha} , h _ { \beta } : \alpha \in \Phi ^ { + } , \beta \in \Sigma \}. \end{equation*}
Thus $\mathbf{l} = | \Sigma |$ is the dimension of $\mathfrak h $. For $\mathfrak{sl}_n ( \mathbf{C} )$ one can choose the root subspaces $\mathfrak { g } _ { \alpha }$ to consist of scalar multiples of matrix units $e_{ij}$, for $i \neq j$ (positive for $i < j$ and negative for $i > j$). The elements $h _ { \beta }$ of the Chevalley basis $\frak B$ of $\mathfrak{sl}_n ( \mathbf{C} )$ are the matrices $e_{ii} - e_{i + 1 i + 1}$ for $1 \leq i \leq n - 1$.
There is a duality between the Euclidean space ${\cal E}^ \operatorname{l}$ containing the root system $\Phi$ (induced by the killing form) and the real space generated by the Chevalley basis of $\mathfrak h $. The elements dual to roots are called co-roots, and the linear functions on $\mathfrak h $ which map the co-roots to integers are called weights. The set of weights is a free $\bf Z$-lattice $\Lambda \supseteq \Phi$ of rank $| \sum |$. A weight whose values on positive co-roots are non-negative is called dominant. The basis of the weight lattice dual to the simple co-roots is the set of fundamental weights.
The toral subalgebra $\mathfrak h $ acts diagonally on every finite-dimensional $\frak g$-module $M$, hence it decomposes into the eigenspaces, called weight spaces $M ( \lambda )$, $\lambda \in \Lambda$. Modules which are generated as $\frak g$-module by a weight vector $v ^ { + }$ of weight $\lambda$ such that all further occurring weights are later in the lexicographic order on $\Lambda$ are called highest weight modules of highest weight $\lambda$. The generator $v ^ { + }$ is called a maximal vector. There are universal highest weight modules, called Verma modules (cf. also Representation of a Lie algebra). They play a role similar to Weyl modules for $G$. Thus, for instance, the Verma module $V ( \lambda )$ to highest weight $\lambda$ is induced from the linear representation of the Borel subalgebra $\mathfrak { b } ^ { + } = \mathfrak { h } \oplus \mathfrak { n } ^ { + }$, setting $\mathfrak { n } ^ { + } = \sum ^{ \oplus }_{ \alpha \in \Phi ^ { + } } \mathfrak { g } _ { \alpha }$, which arises by extending the linear character $\lambda$ of $\mathfrak h $ to ${\frak b} ^ { + }$ with trivial $\mathfrak{n} ^ { + }$-action. Morover, $V ( \lambda )$ admits a contravariant $\frak g$-invariant bilinear form and hence has a unique maximal submodule. The corresponding irreducible factor module $W ( \lambda )$ is a highest weight module with highest weight $\lambda$ and the set of all modules $W ( \lambda )$, where $\lambda$ runs through the set $\Lambda$, is a complete set of irreducible objects in the category $\mathcal{O}$ associated with $\frak g$. Those with dominant highest weight are precisely the finite-dimensional ones. The category $\mathcal{O}$ consists of all $\frak g$-modules which allow a weight space decomposition with finite-dimensional weight spaces and have locally nilpotent $e _ { \alpha }$-action for all $\alpha \in \Phi$. The weight space decomposition of modules $V$ in $\mathcal{O}$ can be encoded in the formal character $\chi _ { V }$. For dominant weights $\lambda$ the formal characters and consequently the dimension of the finite-dimensional irreducible modules $W ( \lambda )$ are known by formulas of Freudenthal, Kostant and Weyl (cf. also Character formula).
Let $V$ be a finite-dimensional $\frak g$-module. Since $\frak g$ is simple, this module affords a faithful representation of $\frak g$. The set $\Lambda ( V )$ of occurring weights lies between the root lattice and the weight lattice $\Lambda$. For $\alpha \in \Phi$ the element $e _ { \alpha }$ of the Chevalley basis $\frak B$ of $\frak g$ acts as a nilpotent endomorphism on $V$. Thus, one can exponentiate its representing matrix, also denoted by $e _ { \alpha }$. One also wants to simultaneously carry out a base change to obtain a transition from $\mathbf{C}$ to an arbitrary field $K$. For this one considers Kostant's $\bf Z$-form $\mathcal{U}_{ \mathbf{Z}}$ in the enveloping algebra $\mathfrak{U} ( \mathfrak{g} )$ of $\frak g$ (cf. also Universal enveloping algebra). This is the $\bf Z$-subalgebra of $\mathfrak{U} ( \mathfrak{g} )$ generated by elements of the form $\left. e _ { \alpha } ^ { i } \middle/ i !\right.$ for $0 \leq i \in \mathbf Z$ and $\alpha \in \Phi$ and elements of the form
\begin{equation*} \left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! } \end{equation*}
for $h = h _ { \beta } \in \frak h$, where $\beta \in \Sigma$. The $K$-algebra $\mathcal{U} _ { K } = K \otimes _\mathbf{Z} \mathcal{U} _ { \mathbf{Z} }$ is called the hyper-algebra, or the divided power algebra, of $\frak g$. One chooses an $\mathcal{U}_{ \mathbf{Z}}$-invariant $\bf Z$-lattice $M$ in $V$. Then for $t \in K$ and $\alpha \in \Phi$ the operator $x _ { \alpha } ( t ) = \sum _ { i = 0 } ^ { \infty } t ^ { i } \otimes e _ { \alpha } ^ { i } / i !$ is a well-defined automorphism of $M _ { K } = K \otimes _ { Z } M$. The group generated by $\{ x _ { \alpha } ( t ) : t \in K , \alpha \in \Phi \}$ is the Chevalley group $G _ { K } ( V )$. If $\Lambda ( V )$ is the root lattice, this group is of adjoint type, if $\Lambda( V ) = \Lambda$, then it is of universal type and, indeed, $G _ { K } ( V ) = G$ is the group started with. Any other Chevalley group over $K$ associated with $\frak g$ is an epimorphic image of $G$. In particular, even if $\Lambda ( V ) \neq \Lambda$, the $K$-space $M _ { K }$ is a $G$-module.
This is applied to the irreducible $\frak g$-module $W ( \lambda )$ for $\lambda \in \Delta ^ { + }$. Let $v ^ { + }$ be a maximal vector in $W ( \lambda )$. Then $M = \mathcal{U} _ { \mathbf{Z} } v ^ { + }$ is an $\mathcal{U}_{ \mathbf{Z}}$-invariant lattice in $W ( \lambda )$ and the $G$-module $M _ { K }$ is the Weyl module $\Delta ( \lambda )$. The weights of $G$ and $\frak g$ coincide, hence Weyl's character formula (and the formula of Freudenthal) describe the formal character of $\Delta ( \lambda )$. The lattice $M$ is minimal among all $\mathcal{U}_{ \mathbf{Z}}$-invariant lattices in $W ( \lambda )$ with the property that it intersects the weight space $W ( \lambda ) ^ { \lambda }$ of $\lambda$ precisely in $\mathbf{Z} v^{+}$. This set also has an upper bound $\widehat{M}$, and $\nabla ( \lambda ) = \hat{M} _ { K }$ as $G$-modules.
Character formulas.
If $K$ is algebraically closed of characteristic $0$, the Weyl modules are irreducible, but this is not true in general for fields $K$ of positive characteristic. However, as in the special case of general linear groups, $\Delta ( \lambda )$ has a unique maximal submodule and the set of factor modules $L ( \lambda )$ is a complete set of non-isomorphic irreducible $K G$-modules.
One of the most outstanding open (1998) problems concerning Weyl modules is to determine the composition factors of those, or, in the language of Brauer theory, to determine the decomposition matrix of $G$. Thus, let $d_{ \lambda \mu }$ be the multiplicity of $L ( \mu )$ as composition factor of $\Delta ( \lambda )$. From Weyl's character formula one sees immediately that $d _ { \lambda \lambda } = 1$ and that $d_{ \lambda \mu } \neq 0$ implies that the partition $\mu$ comes later in the partial order than $\lambda$. Ordering $\Lambda ^ { + }$ lexicographically, the decomposition matrix becomes lower unitriangular. Since the formal characters of Weyl modules are known, the problem of computing the $d_{ \lambda \mu }$ is equivalent to the problem of finding the formal characters of the irreducible $G$-modules $L ( \lambda )$.
There is a similar problem in the representation theory of the Lie algebra $\frak g$ associated with $G$, namely the computation of the composition factors of Verma modules or, equivalently, the computation of the formal character of $W ( \lambda )$ for all $\lambda \in \Lambda$ (and not only for the dominant weights $\lambda$). D. Kazhdan and Lusztig conjectured such a character formula in 1979 in [a7]; it was proven shortly after in [a3] and, independently, in [a4]. The combinatorics in this formula are given by Kazhdan–Lusztig polynomials, which are based on properties of the Hecke algebra, a deformation of the Weyl group of $G$.
The Lusztig conjecture predicts similarly a character formula for Weyl modules in terms of certain Kazhdan–Lusztig polynomials; however, under additional assumptions on the characteristic $p$ of $K$ as well as on the highest weights. If confirmed, one can derive the decomposition numbers of the other Weyl modules too. In [a1], H.H. Andersen, J.C. Jantzen and W. Soergel proved the Lusztig conjecture for large $p$ without determining a concrete bound for $p$. Here is a brief description of the things involved in the proof.
The notion of a category $\mathcal{O}$ can be generalized to Kac–Moody algebras (cf. Kac–Moody algebra) (especially in the affine case), and the Kazhdan–Lusztig conjecture is true here as well by a result of M. Kashiwara and T. Tanisaki, [a10]. There is another remarkable extension of the theory to a new class of objects, called quantum groups, which are deformations involving a parameter $q$ of the hyper-algebra associated with $\frak g$ (or, at least in type $A$, of the coordinate ring of $G$). The representation theory for $\frak g$ extends to those algebras and there is a category $\mathcal{O}$ as well. In a series of papers [a8], [a9], Kazhdan and Lusztig produced an equivalence between a certain category $\mathcal{O}$ for affine Kac–Moody algebras and the category $\mathcal{O}$ of quantum groups, where the parameter $q$ is specialized to a root of unity. As a consequence they showed that the Lusztig conjecture holds for quantum groups in characteristic $0$ at roots of unity. But this case appears to be lying in between the characteristic-$0$ theory of category $\mathcal{O}$ and the characteristic-$p$ theory of representations of $G$. Andersen, Jantzen and Soergel found a (very elaborate) method to compare representations of quantum groups at $p$th roots of unity with those of algebraic groups in characteristic $p$, which finally lead to their result [a1].
The formal characters of the irreducible representations of quantum groups at roots of unity or, equivalently, the decomposition multiplicities of irreducible modules in $q$-Weyl modules can be computed using character formulas for tilting modules, which are, by definition, modules which have a filtrations by Weyl and induced modules. Soergel used the Kashiwara–Tanisaki and the Kazhdan–Lusztig results to derive in [a14], [a15] character formulas for indecomposable tilting modules. Those give another basis of the Grothendieck group and his approach provides a much faster algorithm to compute the decomposition matrices of quantum groups at roots of unity in characteristic $0$ (at least in the simply laced case and conjecturally in general).
When computing the crystal basis of the Fock space, A. Lascoux, B. Leclerc and J.-Y. Thibon noticed an astonishing coincidence of their calculations with decomposition tables for general linear groups and symmetric groups, and conjectured in [a11] that one can derive the decomposition matrices of quantum groups of type $A$ over fields of characteristic $0$ (or, equivalently, of $q$-Schur algebras, defined by R. Dipper and G. James as $q$-deformations of Schur algebras $S ( n , r )$, see [a18], [a19]) at roots of unity by comparing the standard and the crystal basis of Fock space. This conjecture was extended and proved by S. Ariki in [a2], [a16]. The concrete computation is given again by evaluating certain polynomials at one. It is remarkable that those have non-negative integral coefficients. It is conjectured that these have a deeper meaning: They should give the composition multiplicities of the various layers in the Jantzen filtration of the $q$-Weyl modules.
References
| [a1] | H.H. Andersen, J.C. Jantzen, W. Soergel, "Representations of quantum groups at a $p$-th root of unity and of semisimple groups in characteristic $p$: Independence of $p$" Astérisque , 220 (1994) pp. 1–321 MR1272539 |
| [a2] | S. Ariki, "On the decomposition numbers of the Hecke algebra of $G ( m , 1 , n )$" J. Math. Kyoto Univ. , 36 : 4 (1996) pp. 789–808 MR1443748 Zbl 0888.20011 |
| [a3] | A.A. Beilinson, I.N. Bernstein, "Localisation de $g$-modules" C.R. Acad. Sci. Paris Ser. I Math. , 292 : 1 (1981) pp. 15–18 MR610137 |
| [a4] | J.L. Brylinski, M. Kashiwara, "Kazhdan Lusztig conjecture and holonomic systems" Invent. Math. , 64 : 3 (1981) pp. 387–410 MR0632980 Zbl 0473.22009 |
| [a5] | R. Carter, G. Lusztig, "On the modular representations of the general linear and symmetric groups" Math. Z. , 136 (1974) pp. 193–242 MR0369503 MR0354887 Zbl 0301.20005 Zbl 0298.20009 |
| [a6] | J.A. Green, "Polynomial representations of $GL_n$" , Lecture Notes Math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 |
| [a7] | D. Kazhdan, G. Lusztig, "Representations of Coxeter groups and Hecke algebras" Invent. Math. , 53 : 2 (1979) pp. 165–184 MR0560412 Zbl 0499.20035 |
| [a8] | D. Kazhdan, G. Lusztig, "Affine Lie algebras and quantum groups" Duke Math. J. , 62 (1991) (Also: Internat. Math. Res. Notices 2 (1991), 21-29) MR1104840 Zbl 0726.17015 |
| [a9] | D. Kazhdan, G. Lusztig, "Tensor structures arising from affine Lie algebras I-III, III-IV" J. Amer. Math. Soc. , 6–7 (1993/94) pp. 905–1011; 335–453 |
| [a10] | M. Kashiwara, T. Tanisaki, "Kazhdan–Lusztig conjecture for affine Lie algebras with negative level. I,II" Duke Math. J. , 77–84 (1995-1996) pp. 21–62; 771–81 MR1408544 MR1317626 |
| [a11] | A. Lascoux, B. Leclerc, J.-Y. Thibon, "Hecke algebras at roots of unity and crystal bases of quantum affine algebras" Comm. Math. Phys. , 181 : 1 (1996) pp. 205–263 MR1410572 Zbl 0874.17009 |
| [a12] | I. Schur, "Uber eine Klasse von Matrizen, die sich einer gegebenen Matrix zuordnen lassen (1901)" , I. Schur, Gesammelte Abhandlungen I , Springer (1973) pp. 1–70 |
| [a13] | I. Schur, "Uber die rationalen Darstellungen der allgemeinen linearen Gruppe (1927)" , I. Schur, Gesammelte Abhandlungen III , Springer (1973) pp. 68–85 |
| [a14] | W. Soergel, "Charakterformeln für Kipp–Moduln über Kac–Moody–Algebren" Represent. Theory , 1 (1997) pp. 115–132 (Electronic},) Zbl 0964.17019 |
| [a15] | W. Soergel, "Kazhdan–Lusztig polynomials and a combinatoric[s] for tilting modules" Represent. Theory , 1 (1997) pp. 83–114 MR1444322 |
| [a16] | M. Varagnolo, E. Vasserot, "Canonical bases and Lusztig conjecture for quantized sl(N) at roots of unity" Preprint (1998) (math.QA/9803023) |
| [a17] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1966) MR0000255 Zbl 1024.20501 Zbl 1024.20502 Zbl 0020.20601 Zbl 65.0058.02 |
| [a18] | R. Dipper, G. James, "The $q$-Schur algebra" Proc. London Math. Soc. , 59 (1989) pp. 23–50 MR997250 |
| [a19] | R. Dipper, G. James, "$q$-Tensor space and $q$-Weyl modules" Trans. Amer. Math. Soc. , 327 (1991) pp. 251–282 MR1012527 |
Weyl module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_module&oldid=54341