Difference between revisions of "Weyl almost-periodic functions"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | The class | + | {{TEX|done}} |
| + | The class $W^p$ of complex-valued functions $f(x)$, $-\infty<x<\infty$, summable to degree $p$ on each bounded interval of the real axis and such that for every $\epsilon>0$ there is an $l=l(\epsilon,f)$ for which $f$ has a relatively-dense set $S_l^p$ of $\epsilon$-almost-periods (cf. [[Almost-period|Almost-period]]). The class was defined by H. Weyl [[#References|[1]]]. The class $W^p$ of Weyl almost-periodic functions is an extension of the class of [[Stepanov almost-periodic functions|Stepanov almost-periodic functions]]. | ||
Weyl almost-periodic functions are related to the metric | Weyl almost-periodic functions are related to the metric | ||
| − | + | $$D_{W^p}(f,g)=\left\lbrace\lim_{l\to\infty}\sup_{-\infty<x<\infty}\frac{1}{2l}\int\limits_{x-l}^{x+l}|f(t)-g(t)|^pdt\right\rbrace^{1/p}.$$ | |
| − | If | + | If $\phi$ is a null function in the metric $D_{W^p}$, i.e. |
| − | + | $$\lim_{l\to\infty}\sup_x\frac{1}{2l}\int\limits_{x-l}^{x+l}|\phi(t)|^pdt=0,$$ | |
| − | and | + | and $f$ is a Stepanov almost-periodic function, then |
| − | + | $$f+\phi\tag{*}$$ | |
| − | is a Weyl almost-periodic function. There also exist Weyl almost-periodic functions which cannot be represented in the form | + | is a Weyl almost-periodic function. There also exist Weyl almost-periodic functions which cannot be represented in the form \ref{*}; cf. [[#References|[3]]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Weyl, "Integralgleichungen und fastperiodische Funktionen" ''Math. Ann.'' , '''97''' (1927) pp. 338–356</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.M. Levitan, V.V. Stepanov, "Sur les fonctions presque périodiques apportenant au sens strict à la classe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097680/w09768017.png" />" ''Dokl. Akad. Nauk SSSR'' , '''22''' : 5 (1939) pp. 220–223</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Weyl, "Integralgleichungen und fastperiodische Funktionen" ''Math. Ann.'' , '''97''' (1927) pp. 338–356</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.M. Levitan, V.V. Stepanov, "Sur les fonctions presque périodiques apportenant au sens strict à la classe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097680/w09768017.png" />" ''Dokl. Akad. Nauk SSSR'' , '''22''' : 5 (1939) pp. 220–223</TD></TR></table> | ||
Latest revision as of 13:45, 16 October 2014
The class $W^p$ of complex-valued functions $f(x)$, $-\infty<x<\infty$, summable to degree $p$ on each bounded interval of the real axis and such that for every $\epsilon>0$ there is an $l=l(\epsilon,f)$ for which $f$ has a relatively-dense set $S_l^p$ of $\epsilon$-almost-periods (cf. Almost-period). The class was defined by H. Weyl [1]. The class $W^p$ of Weyl almost-periodic functions is an extension of the class of Stepanov almost-periodic functions.
Weyl almost-periodic functions are related to the metric
$$D_{W^p}(f,g)=\left\lbrace\lim_{l\to\infty}\sup_{-\infty<x<\infty}\frac{1}{2l}\int\limits_{x-l}^{x+l}|f(t)-g(t)|^pdt\right\rbrace^{1/p}.$$
If $\phi$ is a null function in the metric $D_{W^p}$, i.e.
$$\lim_{l\to\infty}\sup_x\frac{1}{2l}\int\limits_{x-l}^{x+l}|\phi(t)|^pdt=0,$$
and $f$ is a Stepanov almost-periodic function, then
$$f+\phi\tag{*}$$
is a Weyl almost-periodic function. There also exist Weyl almost-periodic functions which cannot be represented in the form \ref{*}; cf. [3].
References
| [1] | H. Weyl, "Integralgleichungen und fastperiodische Funktionen" Math. Ann. , 97 (1927) pp. 338–356 |
| [2] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian) |
| [3] | B.M. Levitan, V.V. Stepanov, "Sur les fonctions presque périodiques apportenant au sens strict à la classe 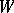 " Dokl. Akad. Nauk SSSR , 22 : 5 (1939) pp. 220–223 " Dokl. Akad. Nauk SSSR , 22 : 5 (1939) pp. 220–223 |
Weyl almost-periodic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_almost-periodic_functions&oldid=33675