Difference between revisions of "Weil-Châtelet group"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | w0975901.png | ||
| + | $#A+1 = 43 n = 4 | ||
| + | $#C+1 = 43 : ~/encyclopedia/old_files/data/W097/W.0907590 Weil\ANDCh\Awatelet group | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The group of principal homogeneous spaces (cf. [[Principal homogeneous space|Principal homogeneous space]]) over an Abelian variety. It was shown by A. Weil [[#References|[1]]] and, in one special case, by F. Châtelet, that for an arbitrary Abelian variety $ A $ | |
| + | over a field $ k $, | ||
| + | the set $ { \mathop{\rm WC} } ( A, k) $ | ||
| + | of principal homogeneous spaces over $ A $, | ||
| + | defined over k, has a group structure. The group $ { \mathop{\rm WC} } ( A, k) $ | ||
| + | is isomorphic to the first [[Galois cohomology|Galois cohomology]] group $ H ^ {1} ( k, A) $. | ||
| + | The group $ { \mathop{\rm WC} } ( A, k) $ | ||
| + | is always periodic; moreover, if $ k = \mathbf Q $, | ||
| + | it contains elements of arbitrary orders [[#References|[4]]], [[#References|[5]]]. According to Lang's theorem, $ { \mathop{\rm WC} } ( A, k) = 0 $ | ||
| + | if $ k $ | ||
| + | is a finite field. The index $ I = { \mathop{\rm ind} } _ {k} ( D) $, | ||
| + | equal to the smallest degree of an extension $ K/k $ | ||
| + | for which there exists a $ K $- | ||
| + | rational point $ D $, | ||
| + | is defined for any element $ D \in { \mathop{\rm WC} } ( A, k) $. | ||
| + | If $ { \mathop{\rm dim} } A = 1 $ | ||
| + | and $ k $ | ||
| + | is an algebraic function field over an algebraically closed field of constants or a local field, $ I $ | ||
| + | becomes identical with the order of $ D $ | ||
| + | in the group $ { \mathop{\rm WC} } ( A, k) $[[#References|[6]]], [[#References|[10]]]. In the general case these numbers are different, but $ { \mathop{\rm ord} } ( D) $ | ||
| + | is always a divisor of $ I $[[#References|[7]]]. The group $ { \mathop{\rm WC} } ( A, k) $ | ||
| + | has been computed for local fields $ k $( | ||
| + | see, for instance, [[#References|[6]]], [[#References|[8]]], [[#References|[9]]]). | ||
| − | + | If $ k $ | |
| + | is a global field, the computation of the group $ { \mathop{\rm WC} } ( A, k) $ | ||
| + | is based on the reduction homomorphisms | ||
| − | + | $$ | |
| + | \phi _ {v} : \mathop{\rm WC} ( A, k ) \rightarrow \mathop{\rm WC} ( A, k _ {v} ), | ||
| + | $$ | ||
| − | known as the Tate–Shafarevich group of the Abelian variety | + | where $ v $ |
| + | is an arbitrary valuation of $ k $ | ||
| + | and $ k _ {v} $ | ||
| + | is the completion of $ k $ | ||
| + | with respect to $ v $. | ||
| + | The kernel $ {\mathop{\amalg\kern-0.30em\amalg}} ( A) $ | ||
| + | of the homomorphism | ||
| + | |||
| + | $$ | ||
| + | \phi = \sum \phi _ {v} : \mathop{\rm WC} ( A, k) \rightarrow \sum _ { v } | ||
| + | \mathop{\rm WC} ( A, k _ {v} ), | ||
| + | $$ | ||
| + | |||
| + | known as the Tate–Shafarevich group of the Abelian variety $ A $, | ||
| + | has been computed only in the case when $ k $ | ||
| + | is a field of algebraic functions of one variable over an algebraically closed field of constants [[#References|[5]]], [[#References|[8]]], [[#References|[11]]]. The co-kernel of $ \phi $ | ||
| + | has also been described in this case (up to the $ p $- | ||
| + | component, where $ p $ | ||
| + | is the characteristic of $ k $). | ||
| + | The results of these calculations are used in the theory of elliptic surfaces. If $ k $ | ||
| + | is an algebraic number field, the structure of the group $ {\mathop{\amalg\kern-0.30em\amalg}} ( A) $ | ||
| + | has not been studied to any great extent. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Weil, "On algebraic groups and homogeneous spaces" ''Amer. J. Math.'' , '''77''' (1955) pp. 493–512 {{MR|0074084}} {{ZBL|0065.14202}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.I. Bashmakov, "Cohomology of Abelian varieties over a number field" ''Russian Math. Surveys'' , '''27''' : 6 (1972) pp. 25–70 ''Uspekhi Mat. Nauk'' , '''27''' : 6 (1972) pp. 25–66</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Cassels, "Diophantine equations with special reference to elliptic curves" ''J. London Math. Soc.'' , '''41''' (1966) pp. 193–291 {{MR|0199150}} {{ZBL|0138.27002}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.R. Shafarevich, "Birational equivalence of elliptic curves" ''Dokl. Akad. Nauk SSSR'' , '''114''' : 2 (1957) pp. 267–270 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.R. Shafarevich, "Exponents of elliptic curves" ''Dokl. Akad. Nauk SSSR'' , '''114''' : 4 (1957) pp. 714–716 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I.R. Shafarevich, "Principal homogeneous spaces defined over a function field" ''Trudy Mat. Inst. Steklov.'' , '''64''' (1961) pp. 316–346 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S. Lang, J. Tate, "Principal homogeneous spaces over abelian varieties" ''Amer. J. Math.'' , '''80''' (1958) pp. 659–684 {{MR|0106226}} {{ZBL|0097.36203}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.P. Ogg, "Cohomology of Abelian varieties over function fields" ''Ann. of Math. (2)'' , '''76''' : 2 (1962) pp. 185–212</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J.T. Tate, "WC-groups over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759043.png" />-adic fields" , ''Sem. Bourbaki'' , '''Exp. 156''' , Secr. Math. Univ. Paris (1957)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. Lichtenbaum, "The period-index problem for elliptic curves" ''Amer. J. Math.'' , '''90''' : 4 (1968) pp. 1209–1223</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> M. Raynaud, "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes (d'après Ogg–Shafarévitch et Grothendieck)" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , ''Dix exposés sur la cohomologie des schémas'' , North-Holland & Masson (1968) pp. 12–30</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Weil, "On algebraic groups and homogeneous spaces" ''Amer. J. Math.'' , '''77''' (1955) pp. 493–512 {{MR|0074084}} {{ZBL|0065.14202}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.I. Bashmakov, "Cohomology of Abelian varieties over a number field" ''Russian Math. Surveys'' , '''27''' : 6 (1972) pp. 25–70 ''Uspekhi Mat. Nauk'' , '''27''' : 6 (1972) pp. 25–66</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Cassels, "Diophantine equations with special reference to elliptic curves" ''J. London Math. Soc.'' , '''41''' (1966) pp. 193–291 {{MR|0199150}} {{ZBL|0138.27002}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.R. Shafarevich, "Birational equivalence of elliptic curves" ''Dokl. Akad. Nauk SSSR'' , '''114''' : 2 (1957) pp. 267–270 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.R. Shafarevich, "Exponents of elliptic curves" ''Dokl. Akad. Nauk SSSR'' , '''114''' : 4 (1957) pp. 714–716 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> I.R. Shafarevich, "Principal homogeneous spaces defined over a function field" ''Trudy Mat. Inst. Steklov.'' , '''64''' (1961) pp. 316–346 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S. Lang, J. Tate, "Principal homogeneous spaces over abelian varieties" ''Amer. J. Math.'' , '''80''' (1958) pp. 659–684 {{MR|0106226}} {{ZBL|0097.36203}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.P. Ogg, "Cohomology of Abelian varieties over function fields" ''Ann. of Math. (2)'' , '''76''' : 2 (1962) pp. 185–212</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> J.T. Tate, "WC-groups over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759043.png" />-adic fields" , ''Sem. Bourbaki'' , '''Exp. 156''' , Secr. Math. Univ. Paris (1957)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. Lichtenbaum, "The period-index problem for elliptic curves" ''Amer. J. Math.'' , '''90''' : 4 (1968) pp. 1209–1223</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> M. Raynaud, "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes (d'après Ogg–Shafarévitch et Grothendieck)" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , ''Dix exposés sur la cohomologie des schémas'' , North-Holland & Masson (1968) pp. 12–30</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The Tate–Shafarevich group of certain elliptic curves over number fields has been recently computed ([[#References|[a1]]], [[#References|[a2]]], [[#References|[a5]]]). Also, some new results on the | + | The Tate–Shafarevich group of certain elliptic curves over number fields has been recently computed ([[#References|[a1]]], [[#References|[a2]]], [[#References|[a5]]]). Also, some new results on the $ p $- |
| + | component of the Weil–Châtelet groups have been obtained [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.A. Kolyvagin, "Finiteness of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759045.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759046.png" /> for a class of Weil curves" ''Math. USSR Izv.'' , '''32''' (1989) pp. 523–541 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''52''' (1988) pp. 522–540</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.A. Kolyvagin, "On the structure of Shafarevich–Tate groups" S. Block (ed.) et al. (ed.) , ''Algebraic geometry'' , ''Lect. notes in math.'' , '''1479''' , Springer (1991) pp. 94–121 {{MR|1181210}} {{ZBL|0753.14025}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Milne, "Arithmetic duality theorems" , Acad. Press (1986)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986) {{MR|0817210}} {{ZBL|0585.14026}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Rubin, "Tate–Shafarevich groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759047.png" />-functions of elliptic curves with complex multiplication" ''Invert. Math.'' , '''89''' (1987) pp. 527–560 {{MR|0903383}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> V.A. Kolyvagin, "Euler systems" P. Cartier (ed.) et al. (ed.) , ''Grothendieck Festschrift'' , '''II''' , Birkhäuser (1990) pp. 435–484</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> K. Rubin, "The work of Kolyvagin on the arithmetic of elliptic curves" W.P. Barth (ed.) et al. (ed.) , ''Arithmetic of Complex Manifolds'' , ''Lect. notes in math.'' , '''1399''' , Springer (1989) pp. 128–136</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.A. Kolyvagin, "Finiteness of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759045.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759046.png" /> for a class of Weil curves" ''Math. USSR Izv.'' , '''32''' (1989) pp. 523–541 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''52''' (1988) pp. 522–540</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.A. Kolyvagin, "On the structure of Shafarevich–Tate groups" S. Block (ed.) et al. (ed.) , ''Algebraic geometry'' , ''Lect. notes in math.'' , '''1479''' , Springer (1991) pp. 94–121 {{MR|1181210}} {{ZBL|0753.14025}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Milne, "Arithmetic duality theorems" , Acad. Press (1986)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986) {{MR|0817210}} {{ZBL|0585.14026}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Rubin, "Tate–Shafarevich groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097590/w09759047.png" />-functions of elliptic curves with complex multiplication" ''Invert. Math.'' , '''89''' (1987) pp. 527–560 {{MR|0903383}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> V.A. Kolyvagin, "Euler systems" P. Cartier (ed.) et al. (ed.) , ''Grothendieck Festschrift'' , '''II''' , Birkhäuser (1990) pp. 435–484</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> K. Rubin, "The work of Kolyvagin on the arithmetic of elliptic curves" W.P. Barth (ed.) et al. (ed.) , ''Arithmetic of Complex Manifolds'' , ''Lect. notes in math.'' , '''1399''' , Springer (1989) pp. 128–136</TD></TR></table> | ||
Revision as of 08:29, 6 June 2020
The group of principal homogeneous spaces (cf. Principal homogeneous space) over an Abelian variety. It was shown by A. Weil [1] and, in one special case, by F. Châtelet, that for an arbitrary Abelian variety $ A $
over a field $ k $,
the set $ { \mathop{\rm WC} } ( A, k) $
of principal homogeneous spaces over $ A $,
defined over k, has a group structure. The group $ { \mathop{\rm WC} } ( A, k) $
is isomorphic to the first Galois cohomology group $ H ^ {1} ( k, A) $.
The group $ { \mathop{\rm WC} } ( A, k) $
is always periodic; moreover, if $ k = \mathbf Q $,
it contains elements of arbitrary orders [4], [5]. According to Lang's theorem, $ { \mathop{\rm WC} } ( A, k) = 0 $
if $ k $
is a finite field. The index $ I = { \mathop{\rm ind} } _ {k} ( D) $,
equal to the smallest degree of an extension $ K/k $
for which there exists a $ K $-
rational point $ D $,
is defined for any element $ D \in { \mathop{\rm WC} } ( A, k) $.
If $ { \mathop{\rm dim} } A = 1 $
and $ k $
is an algebraic function field over an algebraically closed field of constants or a local field, $ I $
becomes identical with the order of $ D $
in the group $ { \mathop{\rm WC} } ( A, k) $[6], [10]. In the general case these numbers are different, but $ { \mathop{\rm ord} } ( D) $
is always a divisor of $ I $[7]. The group $ { \mathop{\rm WC} } ( A, k) $
has been computed for local fields $ k $(
see, for instance, [6], [8], [9]).
If $ k $ is a global field, the computation of the group $ { \mathop{\rm WC} } ( A, k) $ is based on the reduction homomorphisms
$$ \phi _ {v} : \mathop{\rm WC} ( A, k ) \rightarrow \mathop{\rm WC} ( A, k _ {v} ), $$
where $ v $ is an arbitrary valuation of $ k $ and $ k _ {v} $ is the completion of $ k $ with respect to $ v $. The kernel $ {\mathop{\amalg\kern-0.30em\amalg}} ( A) $ of the homomorphism
$$ \phi = \sum \phi _ {v} : \mathop{\rm WC} ( A, k) \rightarrow \sum _ { v } \mathop{\rm WC} ( A, k _ {v} ), $$
known as the Tate–Shafarevich group of the Abelian variety $ A $, has been computed only in the case when $ k $ is a field of algebraic functions of one variable over an algebraically closed field of constants [5], [8], [11]. The co-kernel of $ \phi $ has also been described in this case (up to the $ p $- component, where $ p $ is the characteristic of $ k $). The results of these calculations are used in the theory of elliptic surfaces. If $ k $ is an algebraic number field, the structure of the group $ {\mathop{\amalg\kern-0.30em\amalg}} ( A) $ has not been studied to any great extent.
References
| [1] | A. Weil, "On algebraic groups and homogeneous spaces" Amer. J. Math. , 77 (1955) pp. 493–512 MR0074084 Zbl 0065.14202 |
| [2] | M.I. Bashmakov, "Cohomology of Abelian varieties over a number field" Russian Math. Surveys , 27 : 6 (1972) pp. 25–70 Uspekhi Mat. Nauk , 27 : 6 (1972) pp. 25–66 |
| [3] | J. Cassels, "Diophantine equations with special reference to elliptic curves" J. London Math. Soc. , 41 (1966) pp. 193–291 MR0199150 Zbl 0138.27002 |
| [4] | I.R. Shafarevich, "Birational equivalence of elliptic curves" Dokl. Akad. Nauk SSSR , 114 : 2 (1957) pp. 267–270 (In Russian) |
| [5] | I.R. Shafarevich, "Exponents of elliptic curves" Dokl. Akad. Nauk SSSR , 114 : 4 (1957) pp. 714–716 (In Russian) |
| [6] | I.R. Shafarevich, "Principal homogeneous spaces defined over a function field" Trudy Mat. Inst. Steklov. , 64 (1961) pp. 316–346 (In Russian) |
| [7] | S. Lang, J. Tate, "Principal homogeneous spaces over abelian varieties" Amer. J. Math. , 80 (1958) pp. 659–684 MR0106226 Zbl 0097.36203 |
| [8] | A.P. Ogg, "Cohomology of Abelian varieties over function fields" Ann. of Math. (2) , 76 : 2 (1962) pp. 185–212 |
| [9] | J.T. Tate, "WC-groups over 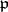 -adic fields" , Sem. Bourbaki , Exp. 156 , Secr. Math. Univ. Paris (1957) -adic fields" , Sem. Bourbaki , Exp. 156 , Secr. Math. Univ. Paris (1957) |
| [10] | S. Lichtenbaum, "The period-index problem for elliptic curves" Amer. J. Math. , 90 : 4 (1968) pp. 1209–1223 |
| [11] | M. Raynaud, "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes (d'après Ogg–Shafarévitch et Grothendieck)" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 12–30 |
Comments
The Tate–Shafarevich group of certain elliptic curves over number fields has been recently computed ([a1], [a2], [a5]). Also, some new results on the $ p $- component of the Weil–Châtelet groups have been obtained [a3].
References
| [a1] | V.A. Kolyvagin, "Finiteness of 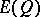 and and 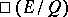 for a class of Weil curves" Math. USSR Izv. , 32 (1989) pp. 523–541 Izv. Akad. Nauk SSSR Ser. Mat. , 52 (1988) pp. 522–540 for a class of Weil curves" Math. USSR Izv. , 32 (1989) pp. 523–541 Izv. Akad. Nauk SSSR Ser. Mat. , 52 (1988) pp. 522–540 |
| [a2] | V.A. Kolyvagin, "On the structure of Shafarevich–Tate groups" S. Block (ed.) et al. (ed.) , Algebraic geometry , Lect. notes in math. , 1479 , Springer (1991) pp. 94–121 MR1181210 Zbl 0753.14025 |
| [a3] | J. Milne, "Arithmetic duality theorems" , Acad. Press (1986) |
| [a4] | J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986) MR0817210 Zbl 0585.14026 |
| [a5] | K. Rubin, "Tate–Shafarevich groups and 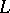 -functions of elliptic curves with complex multiplication" Invert. Math. , 89 (1987) pp. 527–560 MR0903383 -functions of elliptic curves with complex multiplication" Invert. Math. , 89 (1987) pp. 527–560 MR0903383 |
| [a6] | V.A. Kolyvagin, "Euler systems" P. Cartier (ed.) et al. (ed.) , Grothendieck Festschrift , II , Birkhäuser (1990) pp. 435–484 |
| [a7] | K. Rubin, "The work of Kolyvagin on the arithmetic of elliptic curves" W.P. Barth (ed.) et al. (ed.) , Arithmetic of Complex Manifolds , Lect. notes in math. , 1399 , Springer (1989) pp. 128–136 |
Weil-Châtelet group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil-Ch%C3%A2telet_group&oldid=49198