Weakly infinite-dimensional space
A topological space  such that for any infinite system of pairs of closed subsets
such that for any infinite system of pairs of closed subsets 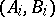 of it,
of it,
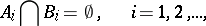 |
there are partitions (cf. Partition) 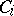 (between
(between 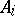 and
and  ) such that
) such that 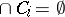 . An infinite-dimensional space which is not weakly infinite dimensional is called strongly infinite dimensional. Weakly infinite-dimensional spaces are also called
. An infinite-dimensional space which is not weakly infinite dimensional is called strongly infinite dimensional. Weakly infinite-dimensional spaces are also called 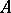 -weakly infinite dimensional. If in the above definition it is further required that some finite subfamily of the
-weakly infinite dimensional. If in the above definition it is further required that some finite subfamily of the 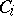 's have empty intersection, one obtains the concept of an
's have empty intersection, one obtains the concept of an  -weakly infinite-dimensional space.
-weakly infinite-dimensional space.
References
| [1] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
Comments
In addition to the above, 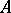 -weakly stands for Aleksandrov weakly, and
-weakly stands for Aleksandrov weakly, and 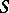 -weakly for Smirnov weakly. There is also the obsolete notion of Hurewicz-weakly infinite-dimensional space. Cf. the survey [a1].
-weakly for Smirnov weakly. There is also the obsolete notion of Hurewicz-weakly infinite-dimensional space. Cf. the survey [a1].
To avoid ambiguity in the phrase "infinite-dimensional space" , the space  could be required to be metrizable, cf. [a2].
could be required to be metrizable, cf. [a2].
References
| [a1] | P.S. Aleksandrov, "Some results in the theory of topological spaces, obtained within the last twenty-five years" Russian Math. Surveys , 15 : 2 (1960) pp. 23–83 Uspekhi Mat. Nauk , 15 : 2 (1960) pp. 25–95 |
| [a2] | J. van Mill, "Infinite-dimensional topology, prerequisites and introduction" , North-Holland (1989) pp. 40 |
| [a3] | R. Engelking, E. Pol, "Countable-dimensional spaces: a survey" Diss. Math. , 216 (1983) pp. 5–41 |
Weakly infinite-dimensional space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weakly_infinite-dimensional_space&oldid=12749