Difference between revisions of "Wall invariant"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | w0970301.png | ||
| + | $#A+1 = 51 n = 1 | ||
| + | $#C+1 = 51 : ~/encyclopedia/old_files/data/W097/W.0907030 Wall invariant | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
An element of the [[Wall group|Wall group]], representing the [[Obstruction|obstruction]] to the surgery of a [[Bordism|bordism]] to a simple homotopy equivalence. | An element of the [[Wall group|Wall group]], representing the [[Obstruction|obstruction]] to the surgery of a [[Bordism|bordism]] to a simple homotopy equivalence. | ||
| − | Let | + | Let $ X $ |
| + | be a finite [[Poincaré complex|Poincaré complex]], $ \nu $ | ||
| + | a fibre bundle over $ X $ | ||
| + | and $ x = [( M, \phi , F )] \in \Omega ( X, \nu ) $ | ||
| + | a bordism class, where $ m $ | ||
| + | is the formal dimension of $ X $ | ||
| + | and $ \phi : M \rightarrow X $ | ||
| + | has degree 1. This mapping can always be represented by an $ [ m/2] $- | ||
| + | connected mapping using a finite sequence of surgeries. Let $ \Lambda = Z [ \pi _ {1} ( X)] $ | ||
| + | be a group ring and let $ \overline{ {}}\; $ | ||
| + | be the involution on $ \Lambda $ | ||
| + | given by the formula $ \overline{ {\sum _ {g} n ( g) g }}\; = \sum w ( g) n ( g) g ^ {-} 1 $, | ||
| + | where $ w: \pi _ {1} ( X) \rightarrow \{ 1, - 1 \} $ | ||
| + | is defined by the first [[Stiefel–Whitney class|Stiefel–Whitney class]] of $ \nu $. | ||
| + | Put | ||
| − | + | $$ | |
| + | K ^ {*} ( M) = \ | ||
| + | \mathop{\rm coker} ( \phi ^ {*} : H ^ {*} ( X) \rightarrow H ^ {*} ( M)), | ||
| + | $$ | ||
| − | + | $$ | |
| + | K _ {*} ( M) = \mathop{\rm ker} ( \phi _ {*} : H _ {*} ( M) \rightarrow H _ {*} ( X)) | ||
| + | $$ | ||
| − | (coefficients in | + | (coefficients in $ \Lambda $). |
| + | The involution is an anti-isomorphism and there is defined the Wall group $ U _ {n} ( \Lambda ) = L _ {n} ( \pi _ {1} ( X), w) $. | ||
| − | Suppose now that | + | Suppose now that $ m = 2k \geq 4 $. |
| + | Then in the stable free $ \Lambda $- | ||
| + | module $ G = K _ {k} ( M) = \pi _ {k + 1 } ( \phi ) $ | ||
| + | one can choose a basis, and [[Poincaré duality|Poincaré duality]] induces a simple isomorphism $ \lambda : G \rightarrow G ^ {*} = K ^ {k} ( M) $, | ||
| + | where $ ( G, \lambda ) $ | ||
| + | is a $ (- 1) ^ {k} $- | ||
| + | form. One therefore obtains the class $ \Theta _ {2k} ( x) = [( G, \lambda )] \in L _ {2k} ( \pi _ {1} ( X), w) $. | ||
| − | Suppose next that | + | Suppose next that $ m = 2k + 1 \geq 5 $. |
| + | One can choose generators in $ \pi _ {k + 1 } ( \phi ) = K _ {k} ( M; \Lambda ) $ | ||
| + | so that they represent the imbeddings $ f _ {i} : S ^ {k} \times D ^ {k + 1 } \rightarrow M $, | ||
| + | with non-intersecting images, and these images are connected by paths with a base point. Put $ U = \cup _ {i} \mathop{\rm Im} f _ {i} $, | ||
| + | $ M _ {0} = M \setminus \mathop{\rm Int} U $. | ||
| + | Since $ \phi \circ f _ {i} \sim 0 $, | ||
| + | one may replace $ \phi $ | ||
| + | by a homotopy and suppose that $ \phi ( u) = * $. | ||
| + | Because $ X $ | ||
| + | is a Poincaré complex, one can replace $ X $ | ||
| + | by a complex with a unique $ m $- | ||
| + | cell, i.e. one has a Poincaré pair $ ( X _ {0} , S ^ {m + 1 } ) $ | ||
| + | and $ X = X _ {0} \cup e ^ {m} $. | ||
| + | By the choice of a suitable cellular approximation one obtains a mapping for the Poincaré triad of degree 1: $ \phi : ( M; M _ {0} , U) \rightarrow ( X; X _ {0} , e ^ {m} ) $. | ||
| + | Consequently one has the diagram of exact sequences: | ||
| − | + | $$ | |
| − | Moreover, one has a non-degenerate pairing | + | Moreover, one has a non-degenerate pairing $ \lambda : K _ {k} ( \partial U) \times K _ {k} ( \partial U) \rightarrow \Lambda $, |
| + | where $ H = ( K _ {k} ( \partial U), \lambda ) $ | ||
| + | is a quadratic $ (- 1) ^ {k} $- | ||
| + | form while $ K _ {k + 1 } ( U, \partial U) $ | ||
| + | and $ K _ {k + 1 } ( M _ {0} , \partial U) $ | ||
| + | define its Lagrange planes $ L $ | ||
| + | and $ P $. | ||
| + | Then $ \Theta _ {2k + 1 } ( x) = [( H; L, P)] \in U _ {2k + 1 } ( \Lambda ) = L _ {2k + 1 } ( \pi _ {1} ( x), w) $. | ||
| − | The elements | + | The elements $ \Theta _ {m} ( x) \in L _ {m} ( \pi _ {1} ( x), w) $ |
| + | defined above are called the Wall invariants. An important property is the independence of $ \Theta ( x) $ | ||
| + | on the choices in the construction and the equivalence of the equation $ \Theta ( x) = 0 $ | ||
| + | to the representability of the class as a simple homotopy equivalence, cf. [[#References|[1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Ranicki, "The algebraic theory of surgery I" ''Proc. London Math. Soc.'' , '''40''' : 1 (1980) pp. 87–192</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.P. Novikov, "Algebraic construction and properties of Hermitian analogs of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097030/w09703052.png" />-theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes I" ''Math. USSR Izv.'' , '''4''' : 2 (1970) pp. 257–292 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''34''' : 2 (1970) pp. 253–288</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Ranicki, "The algebraic theory of surgery I" ''Proc. London Math. Soc.'' , '''40''' : 1 (1980) pp. 87–192</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.P. Novikov, "Algebraic construction and properties of Hermitian analogs of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097030/w09703052.png" />-theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes I" ''Math. USSR Izv.'' , '''4''' : 2 (1970) pp. 257–292 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''34''' : 2 (1970) pp. 253–288</TD></TR></table> | ||
Revision as of 08:28, 6 June 2020
An element of the Wall group, representing the obstruction to the surgery of a bordism to a simple homotopy equivalence.
Let $ X $ be a finite Poincaré complex, $ \nu $ a fibre bundle over $ X $ and $ x = [( M, \phi , F )] \in \Omega ( X, \nu ) $ a bordism class, where $ m $ is the formal dimension of $ X $ and $ \phi : M \rightarrow X $ has degree 1. This mapping can always be represented by an $ [ m/2] $- connected mapping using a finite sequence of surgeries. Let $ \Lambda = Z [ \pi _ {1} ( X)] $ be a group ring and let $ \overline{ {}}\; $ be the involution on $ \Lambda $ given by the formula $ \overline{ {\sum _ {g} n ( g) g }}\; = \sum w ( g) n ( g) g ^ {-} 1 $, where $ w: \pi _ {1} ( X) \rightarrow \{ 1, - 1 \} $ is defined by the first Stiefel–Whitney class of $ \nu $. Put
$$ K ^ {*} ( M) = \ \mathop{\rm coker} ( \phi ^ {*} : H ^ {*} ( X) \rightarrow H ^ {*} ( M)), $$
$$ K _ {*} ( M) = \mathop{\rm ker} ( \phi _ {*} : H _ {*} ( M) \rightarrow H _ {*} ( X)) $$
(coefficients in $ \Lambda $). The involution is an anti-isomorphism and there is defined the Wall group $ U _ {n} ( \Lambda ) = L _ {n} ( \pi _ {1} ( X), w) $.
Suppose now that $ m = 2k \geq 4 $. Then in the stable free $ \Lambda $- module $ G = K _ {k} ( M) = \pi _ {k + 1 } ( \phi ) $ one can choose a basis, and Poincaré duality induces a simple isomorphism $ \lambda : G \rightarrow G ^ {*} = K ^ {k} ( M) $, where $ ( G, \lambda ) $ is a $ (- 1) ^ {k} $- form. One therefore obtains the class $ \Theta _ {2k} ( x) = [( G, \lambda )] \in L _ {2k} ( \pi _ {1} ( X), w) $.
Suppose next that $ m = 2k + 1 \geq 5 $. One can choose generators in $ \pi _ {k + 1 } ( \phi ) = K _ {k} ( M; \Lambda ) $ so that they represent the imbeddings $ f _ {i} : S ^ {k} \times D ^ {k + 1 } \rightarrow M $, with non-intersecting images, and these images are connected by paths with a base point. Put $ U = \cup _ {i} \mathop{\rm Im} f _ {i} $, $ M _ {0} = M \setminus \mathop{\rm Int} U $. Since $ \phi \circ f _ {i} \sim 0 $, one may replace $ \phi $ by a homotopy and suppose that $ \phi ( u) = * $. Because $ X $ is a Poincaré complex, one can replace $ X $ by a complex with a unique $ m $- cell, i.e. one has a Poincaré pair $ ( X _ {0} , S ^ {m + 1 } ) $ and $ X = X _ {0} \cup e ^ {m} $. By the choice of a suitable cellular approximation one obtains a mapping for the Poincaré triad of degree 1: $ \phi : ( M; M _ {0} , U) \rightarrow ( X; X _ {0} , e ^ {m} ) $. Consequently one has the diagram of exact sequences:
$$
Moreover, one has a non-degenerate pairing $ \lambda : K _ {k} ( \partial U) \times K _ {k} ( \partial U) \rightarrow \Lambda $, where $ H = ( K _ {k} ( \partial U), \lambda ) $ is a quadratic $ (- 1) ^ {k} $- form while $ K _ {k + 1 } ( U, \partial U) $ and $ K _ {k + 1 } ( M _ {0} , \partial U) $ define its Lagrange planes $ L $ and $ P $. Then $ \Theta _ {2k + 1 } ( x) = [( H; L, P)] \in U _ {2k + 1 } ( \Lambda ) = L _ {2k + 1 } ( \pi _ {1} ( x), w) $.
The elements $ \Theta _ {m} ( x) \in L _ {m} ( \pi _ {1} ( x), w) $ defined above are called the Wall invariants. An important property is the independence of $ \Theta ( x) $ on the choices in the construction and the equivalence of the equation $ \Theta ( x) = 0 $ to the representability of the class as a simple homotopy equivalence, cf. [1].
References
| [1] | C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) |
| [2] | A.A. Ranicki, "The algebraic theory of surgery I" Proc. London Math. Soc. , 40 : 1 (1980) pp. 87–192 |
| [3] | S.P. Novikov, "Algebraic construction and properties of Hermitian analogs of 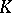 -theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes I" Math. USSR Izv. , 4 : 2 (1970) pp. 257–292 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 2 (1970) pp. 253–288 -theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes I" Math. USSR Izv. , 4 : 2 (1970) pp. 257–292 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 2 (1970) pp. 253–288 |
Wall invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wall_invariant&oldid=17462