Difference between revisions of "Voronoi lattice types"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | Types of point lattices (cf. [[Lattice of points|Lattice of points]]) in | + | {{TEX|done}} |
| + | Types of point lattices (cf. [[Lattice of points|Lattice of points]]) in $n$-dimensional Euclidean space $E^n$, introduced in 1908 by G.F. Voronoi [[#References|[1]]] in the context of a problem on parallelohedra. | ||
| − | A set of points | + | A set of points $\epsilon$ in $E^n$ is called an $(r,R)$-system if no point is closer to any other point than the given distance $r>0$, and if any sphere of radius larger than some given $R$ contains at least one point of $\epsilon$. Let $D$ be a convex polyhedron of the Dirichlet domain (or Dirichlet cell) of a point in $\epsilon$, i.e. of the domain of points in space which are no more remote from that point than from all other points in the system. The Dirichlet domains of the points of an $(r,R)$-system $\epsilon$ have pairwise no common interior points, cover the entire space (i.e. form a partitioning) and have entire faces in common (i.e. constitute a normal partitioning). This system $\epsilon$ may be associated with another normal partitioning $\{L\}$, dual to $\{D\}$, into polyhedra $L$ (inscribed in spheres), each one of which is the convex envelope of the points of the system $\epsilon$ corresponding to all $D$ which meet at a vertex of the partitioning $\{D\}$. |
| − | Two | + | Two $n$-dimensional point lattices are of the same Voronoi type if their partitionings $\{L\}$ are affine to each other. If a frame is such that, for sufficiently small changes of its metric parameters (of the scalar squares $a_{ii}$ and scalar products $a_{ik}$ ($i\neq k$) of its vectors), the partitioning of the lattice constructed on the modified frame is obtained from the partitioning $\{L\}$ of the lattice constructed on the initial frame by the same affine transformation which converts the initial into the modified frame, then the frame is called primitive or general. For this it is necessary and sufficient for the partitioning $\{L\}$ of the initial frame to be simplicial. The point $M$ of the space $E^N$ of parameters $a_{ik}$, where $N=n(n+1)/2$, which corresponds to such a frame, is also known as general. A complete linearly connected domain $\Delta$, containing a general point, in which the partitionings $\{L\}$ for all its points are obtained from the partitioning $\{L\}$ for the lattice constructed on the frame corresponding to the point $M$ by the same affine transformation which maps the initial frame into the frames corresponding to the other points is called the type domain of the point $M$. It was shown by Voronoi that the domain $\Delta$ in $E^N$ has the form of a convex polyhedral angle (a gonohedron) with its vertex at the coordinate origin and with a finite number of faces, and that for any given $n$ there exist only a finite number $\psi$ of non-equivalent domains $\Delta$. He also proposed an algorithm by which these could be found [[#References|[1]]]. For $n=1,2,3,4$ the number $\psi$ is 1, 1, 1, 3, respectively. Voronoi also showed that the most general (i.e. not necessarily of Dirichlet type) normal partitioning of $E^n$ into identical convex, parallel polyhedra located such that $n+1$ meet at the vertices (primitive parallelohedra) is an affine image of the partitioning $\{D\}$ for a lattice. Thus he reduced the study of such parallelohedra to the theory of quadratic forms. For non-primitive parallelohedra (i.e. more than $n+1$ parallelohedra meeting at certain vertices), the possibility of their affine transformation into the domain $D$ of a lattice for arbitrary $n$ is still an open question. It is only known that a positive solution exists for $n=2,3,4$. |
| − | The primitive domain | + | The primitive domain $D$ for a two-dimensional lattice is a convex hexagon with a centre of symmetry, inscribed in a circle, and vice versa. In the case of a three-dimensional lattice this is some $14$-gon, which combinatorially resembles a cubo-octahedron with eight hexagonal and six tetragonal faces; each such face has a centre of symmetry such that the segments issuing from its centre into the centres of the faces are perpendicular to the faces and vice versa. The non-primitive domain $D$ for $n=2$ is a rectangle. For $n=3$ it is either a dodecahedron with four hexagonal and eight parallelogrammatic faces, or a parallelogrammatic dodecahedron, or a vertical hexagonal prism with a primitive two-dimensional $D$ as base, or a rectangular parallelepipedon. For $n=4$ there are three primitive $D$ of different Voronoi lattice types, as well as 49 non-primitive ones. The transition to $n=5$ is accompanied by a large jump — 221 different primitive $D$ [[#References|[4]]]. This result was obtained by introducing the new concept of a $C$-type lattice: Lattices with mutually affine one-dimensional skeletons of the partitioning $\{L\}$ rather than affine partitionings themselves, are said to have the same $C$-type. |
====References==== | ====References==== | ||
| Line 13: | Line 14: | ||
====Comments==== | ====Comments==== | ||
| − | Instead of "Dirichlet cell" one also finds the phrases "Voronoi | + | Instead of "Dirichlet cell" one also finds the phrases "Voronoi region", "first Brillouin zone", "Dirichlet–Voronoi region", "Wabenzelle", "honeycomb", "domain of action of z". The partitioning or tiling by the Dirichlet–Voronoi regions is called "Dirichlet–Voronoi tiling", "Dirichlet tiling" or "Voronoi tiling". The Voronoi problem is whether each parallellohedron is the affine image of a Dirichlet–Voronoi region for a lattice. This is true for $n\leq4$, [[#References|[2a]]]. Cf. [[#References|[a3]]], p. 170ff, for further results. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988) {{MR|0920369}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) {{MR|1003606}} {{ZBL|0683.10025}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) {{MR|0893813}} {{ZBL|0611.10017}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1987) {{MR|0857454}} {{ZBL|0601.05001}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B.N. Delone, R.V. Galivlin, N.I. Shtogrin, "The types of Bravais lattices" ''J. Soviet Math.'' , '''4''' : 1 (1975) pp. 79–156 ''Sovrem. Probl. Mat.'' , '''2''' (1973) pp. 119–257 {{MR|0412947}} {{ZBL|0334.50005}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988) {{MR|0920369}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) {{MR|1003606}} {{ZBL|0683.10025}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) {{MR|0893813}} {{ZBL|0611.10017}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1987) {{MR|0857454}} {{ZBL|0601.05001}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B.N. Delone, R.V. Galivlin, N.I. Shtogrin, "The types of Bravais lattices" ''J. Soviet Math.'' , '''4''' : 1 (1975) pp. 79–156 ''Sovrem. Probl. Mat.'' , '''2''' (1973) pp. 119–257 {{MR|0412947}} {{ZBL|0334.50005}} </TD></TR></table> | ||
Latest revision as of 19:28, 2 June 2016
Types of point lattices (cf. Lattice of points) in $n$-dimensional Euclidean space $E^n$, introduced in 1908 by G.F. Voronoi [1] in the context of a problem on parallelohedra.
A set of points $\epsilon$ in $E^n$ is called an $(r,R)$-system if no point is closer to any other point than the given distance $r>0$, and if any sphere of radius larger than some given $R$ contains at least one point of $\epsilon$. Let $D$ be a convex polyhedron of the Dirichlet domain (or Dirichlet cell) of a point in $\epsilon$, i.e. of the domain of points in space which are no more remote from that point than from all other points in the system. The Dirichlet domains of the points of an $(r,R)$-system $\epsilon$ have pairwise no common interior points, cover the entire space (i.e. form a partitioning) and have entire faces in common (i.e. constitute a normal partitioning). This system $\epsilon$ may be associated with another normal partitioning $\{L\}$, dual to $\{D\}$, into polyhedra $L$ (inscribed in spheres), each one of which is the convex envelope of the points of the system $\epsilon$ corresponding to all $D$ which meet at a vertex of the partitioning $\{D\}$.
Two $n$-dimensional point lattices are of the same Voronoi type if their partitionings $\{L\}$ are affine to each other. If a frame is such that, for sufficiently small changes of its metric parameters (of the scalar squares $a_{ii}$ and scalar products $a_{ik}$ ($i\neq k$) of its vectors), the partitioning of the lattice constructed on the modified frame is obtained from the partitioning $\{L\}$ of the lattice constructed on the initial frame by the same affine transformation which converts the initial into the modified frame, then the frame is called primitive or general. For this it is necessary and sufficient for the partitioning $\{L\}$ of the initial frame to be simplicial. The point $M$ of the space $E^N$ of parameters $a_{ik}$, where $N=n(n+1)/2$, which corresponds to such a frame, is also known as general. A complete linearly connected domain $\Delta$, containing a general point, in which the partitionings $\{L\}$ for all its points are obtained from the partitioning $\{L\}$ for the lattice constructed on the frame corresponding to the point $M$ by the same affine transformation which maps the initial frame into the frames corresponding to the other points is called the type domain of the point $M$. It was shown by Voronoi that the domain $\Delta$ in $E^N$ has the form of a convex polyhedral angle (a gonohedron) with its vertex at the coordinate origin and with a finite number of faces, and that for any given $n$ there exist only a finite number $\psi$ of non-equivalent domains $\Delta$. He also proposed an algorithm by which these could be found [1]. For $n=1,2,3,4$ the number $\psi$ is 1, 1, 1, 3, respectively. Voronoi also showed that the most general (i.e. not necessarily of Dirichlet type) normal partitioning of $E^n$ into identical convex, parallel polyhedra located such that $n+1$ meet at the vertices (primitive parallelohedra) is an affine image of the partitioning $\{D\}$ for a lattice. Thus he reduced the study of such parallelohedra to the theory of quadratic forms. For non-primitive parallelohedra (i.e. more than $n+1$ parallelohedra meeting at certain vertices), the possibility of their affine transformation into the domain $D$ of a lattice for arbitrary $n$ is still an open question. It is only known that a positive solution exists for $n=2,3,4$.
The primitive domain $D$ for a two-dimensional lattice is a convex hexagon with a centre of symmetry, inscribed in a circle, and vice versa. In the case of a three-dimensional lattice this is some $14$-gon, which combinatorially resembles a cubo-octahedron with eight hexagonal and six tetragonal faces; each such face has a centre of symmetry such that the segments issuing from its centre into the centres of the faces are perpendicular to the faces and vice versa. The non-primitive domain $D$ for $n=2$ is a rectangle. For $n=3$ it is either a dodecahedron with four hexagonal and eight parallelogrammatic faces, or a parallelogrammatic dodecahedron, or a vertical hexagonal prism with a primitive two-dimensional $D$ as base, or a rectangular parallelepipedon. For $n=4$ there are three primitive $D$ of different Voronoi lattice types, as well as 49 non-primitive ones. The transition to $n=5$ is accompanied by a large jump — 221 different primitive $D$ [4]. This result was obtained by introducing the new concept of a $C$-type lattice: Lattices with mutually affine one-dimensional skeletons of the partitioning $\{L\}$ rather than affine partitionings themselves, are said to have the same $C$-type.
References
| [1] | G.F. Voronoi, "Studies of primitive parallelotopes" , Collected works , 2 , Kiev (1952) pp. 239–368 (In Russian) |
| [2a] | B.N. Delone, "Sur la partition reguliere de l'espace à quatre dimensions" Izv. Akad. Nauk SSSR Ser. 7, Otd. Fiz. Mat. Nauk : 1 (1929) pp. 79–110 |
| [2b] | B.N. Delone, Izv. Akad. Nauk SSSR Ser. 7, Otd. Fiz. Mat. Nauk : 2 (1929) pp. 147–164 |
| [3a] | B.N. Delone, "The geometry of positive quadratic forms" Uspekhi Mat. Nauk : 3 (1937) pp. 16–62 (In Russian) |
| [3b] | B.N. Delone, "The geometry of positive quadratic forms" Uspekhi Mat. Nauk : 4 (1938) pp. 102–164 (In Russian) |
| [4] | S.S. Ryshkov, E.P. Baranovskii, "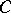 -types of n-dimensional lattices and 5-dimensional primitive parellohedra (with an application to the theory of coverings)" Proc. Steklov Inst. Math. , 137 (1975) Trudy Mat. Inst. Steklov. , 137 (1975) -types of n-dimensional lattices and 5-dimensional primitive parellohedra (with an application to the theory of coverings)" Proc. Steklov Inst. Math. , 137 (1975) Trudy Mat. Inst. Steklov. , 137 (1975) |
Comments
Instead of "Dirichlet cell" one also finds the phrases "Voronoi region", "first Brillouin zone", "Dirichlet–Voronoi region", "Wabenzelle", "honeycomb", "domain of action of z". The partitioning or tiling by the Dirichlet–Voronoi regions is called "Dirichlet–Voronoi tiling", "Dirichlet tiling" or "Voronoi tiling". The Voronoi problem is whether each parallellohedron is the affine image of a Dirichlet–Voronoi region for a lattice. This is true for $n\leq4$, [2a]. Cf. [a3], p. 170ff, for further results.
References
| [a1] | J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988) MR0920369 |
| [a2] | P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989) MR1003606 Zbl 0683.10025 |
| [a3] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) MR0893813 Zbl 0611.10017 |
| [a4] | B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1987) MR0857454 Zbl 0601.05001 |
| [a5] | B.N. Delone, R.V. Galivlin, N.I. Shtogrin, "The types of Bravais lattices" J. Soviet Math. , 4 : 1 (1975) pp. 79–156 Sovrem. Probl. Mat. , 2 (1973) pp. 119–257 MR0412947 Zbl 0334.50005 |
Voronoi lattice types. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Voronoi_lattice_types&oldid=38910