Vietoris homology
One of the first homology theories (cf. Homology theory) defined for the non-polyhedral case. It was first considered by L.E.J. Brouwer in 1911 (for the case of the plane), after which the definition was extended in 1927 by L. Vietoris to arbitrary subsets of Euclidean (and even metric) spaces.
An (ordered)  -dimensional
-dimensional  -simplex
-simplex 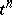 of a subset
of a subset 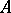 of a metric space
of a metric space 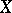 is defined as an ordered subset
is defined as an ordered subset 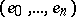 in
in 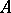 subject to the condition
subject to the condition 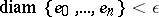 . The
. The  -chains of
-chains of  are then defined for a given coefficient group
are then defined for a given coefficient group 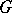 as formal finite linear combinations
as formal finite linear combinations 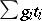 of
of  -simplices
-simplices 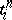 with coefficients
with coefficients 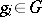 . The boundary of an
. The boundary of an  -simplex
-simplex 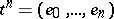 is defined as follows:
is defined as follows: 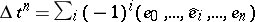 ; this is an
; this is an  -chain. By linearity, the boundary of any
-chain. By linearity, the boundary of any  -chain is defined and
-chain is defined and  -cycles are defined as
-cycles are defined as  -chains with zero boundary. An
-chains with zero boundary. An  -chain
-chain 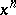 of a set is
of a set is 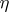 -homologous to zero in
-homologous to zero in 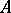 (the notation is
(the notation is 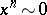 ) if
) if 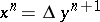 for a certain
for a certain 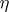 -chain
-chain 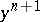 in
in 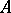 .
.
A true cycle of a set 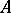 is a sequence
is a sequence 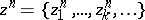 in which
in which 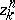 is an
is an 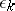 -cycle in
-cycle in 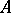 and
and 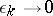 (
(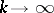 ). The true cycles form a group,
). The true cycles form a group, 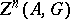 . A true cycle
. A true cycle  is homologous to zero in
is homologous to zero in 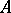 if for any
if for any 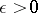 there exists an
there exists an 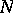 such that all
such that all 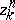 for
for 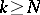 are
are  -homologous to zero in
-homologous to zero in 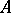 . One denotes by
. One denotes by 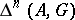 the quotient group of the group
the quotient group of the group 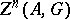 by the subgroup
by the subgroup 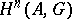 of cycles that are homologous to zero.
of cycles that are homologous to zero.
A cycle  is called convergent if for any
is called convergent if for any 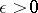 there exists an
there exists an 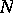 such that any two cycles
such that any two cycles 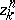 ,
, 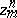 are mutually
are mutually  -homologous in
-homologous in 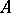 if
if 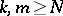 . The group of convergent cycles is denoted by
. The group of convergent cycles is denoted by 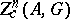 . Let
. Let 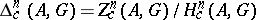 be the corresponding quotient group.
be the corresponding quotient group.
A cycle  has compact support if there exists a compact set
has compact support if there exists a compact set 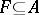 such that all the vertices of all simplices of all cycles
such that all the vertices of all simplices of all cycles 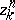 lie in
lie in 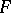 . One similarly modifies the concept of a cycle being homologous to zero by requiring the presence of a compact set on which all the homology-realizing chains lie; convergent cycles with compact support can thus be defined. By denoting with a subscript
. One similarly modifies the concept of a cycle being homologous to zero by requiring the presence of a compact set on which all the homology-realizing chains lie; convergent cycles with compact support can thus be defined. By denoting with a subscript 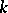 the transition to cycles and homology with compact support, one obtains the groups
the transition to cycles and homology with compact support, one obtains the groups 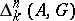 and
and 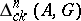 . The latter group is known as the Vietoris homology group. If the polyhedron is finite, the Vietoris homology groups coincide with the standard homology groups.
. The latter group is known as the Vietoris homology group. If the polyhedron is finite, the Vietoris homology groups coincide with the standard homology groups.
Relative homology groups 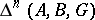 ,
, 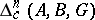 ,
, 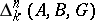 ,
, 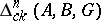 modulo a subset
modulo a subset 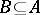 are also defined. An
are also defined. An  -cycle of the set
-cycle of the set 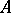 modulo
modulo 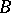 is any
is any  -chain
-chain 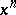 in
in 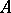 for which the chain
for which the chain 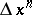 lies in
lies in 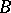 . In a similar manner, an
. In a similar manner, an  -cycle
-cycle 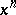 modulo
modulo 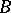 is
is 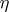 -homologous modulo
-homologous modulo 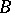 to zero in
to zero in 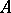 if
if 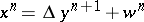 , where
, where 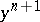 and
and 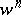 are
are 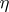 -chains in
-chains in 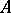 , while the chain
, while the chain 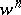 lies in
lies in 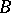 .
.
References
| [1] | P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian) |
Comments
References
| [a1] | J.G. Hocking, G.S. Young, "Topology" , Addison-Wesley (1961) |
Vietoris homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vietoris_homology&oldid=16886