Difference between revisions of "Variance"
m (some tex) |
m (some TeX) |
||
| Line 46: | Line 46: | ||
in the integral case; here $F$ is the distribution function of the random variable $X$, and the integral is understood in the sense of [[Lebesgue-Stieltjes_integral|Lebesgue–Stieltjes]] or [[Riemann–Stieltjes_integral|Riemann–Stieltjes]]. | in the integral case; here $F$ is the distribution function of the random variable $X$, and the integral is understood in the sense of [[Lebesgue-Stieltjes_integral|Lebesgue–Stieltjes]] or [[Riemann–Stieltjes_integral|Riemann–Stieltjes]]. | ||
| − | The variance is not the only conceivable measure of the deviation of a random variable from its expectation. Other measures of the deviation, constructed on the same principle, e.g. $\Ex|X-\Ex X|$, | + | The variance is not the only conceivable measure of the deviation of a random variable from its expectation. Other measures of the deviation, constructed on the same principle, e.g. $\Ex|X-\Ex X|$, $\Ex(X-\Ex X)^4$, etc., are also possible, as are measures of deviation based on quantiles (cf. [[Quantile|Quantile]]). The importance of the variance is mainly due to the role played by this concept in [[Limit theorems|limit theorems]]. Roughly speaking, one may say that if the expectation and variance of the sum of a large number of random variables are known, it is possible to describe completely the distribution law of this sum: It is (approximately) normal, with corresponding parameters (cf. [[Normal distribution|Normal distribution]]). Thus, the most important properties of the variance are connected with the expression for the variance $\Var(X_1+\cdots+X_n)$ of the sum of random variables $X_1,\dots, X_n$: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033330/d03333028.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033330/d03333028.png" /></td> </tr></table> | ||
Revision as of 13:08, 28 February 2013
$\newcommand{\Var}{\operatorname{Var}}$
$\newcommand{\Ex}{\mathop{\mathsf{E}}}$
$\newcommand{\Prob}{\mathop{\mathsf{P}}}$
in probability theory
2020 Mathematics Subject Classification: Primary: 60-01 [MSN][ZBL]
The measure $\Var X$ of the deviation of a random variable $X$ from its mathematical expectation $\Ex X$ defined by the equation: \begin{equation}\label{eq:1} \Var X = \Ex(X-\Ex X)^2. \end{equation}
The properties of the variance are: \begin{equation} \Var X = \Ex X^2 - (\Ex X)^2; \end{equation} if $c$ is a real number, then \begin{equation} \Var (cX) = c^2\Var X, \end{equation} in particular, $\Var(-X) = \Var X$.
In speaking of the variance of a random variable $X$, it is always assumed that its expectation $\Ex X$ exists; the variance $\Var X$ may exist (i.e. be finite) or may not (i.e. be infinite). In modern probability theory the expectation of a random variable is defined in terms of the Lebesgue integral over the sample space. However, formulas expressing the expectation of various functions of a random variable $X$ in terms of the distribution of this variable on the set of real numbers are of importance (cf. Mathematical expectation). For the variance $\Var X$ these formulas are
a) \begin{equation} \Var X = \sum_i(a_i-\Ex X)^2p_i, \end{equation} for a discrete random variable $X$ which assumes at most a countable number of different values $a_i$ with probabilities $p_i=\Prob\{X=a_i\}$;
b) \begin{equation} \Var X = \int\limits_{-\infty}^{\infty}(x-\Ex X)^2p(x)\,dx, \end{equation} for a random variable $X$ with a density $p$ of the probability distribution;
c) \begin{equation} \Var X = \int\limits_{-\infty}^{\infty}(x-\Ex X)^2\,dF(x), \end{equation} in the integral case; here $F$ is the distribution function of the random variable $X$, and the integral is understood in the sense of Lebesgue–Stieltjes or Riemann–Stieltjes.
The variance is not the only conceivable measure of the deviation of a random variable from its expectation. Other measures of the deviation, constructed on the same principle, e.g. $\Ex|X-\Ex X|$, $\Ex(X-\Ex X)^4$, etc., are also possible, as are measures of deviation based on quantiles (cf. Quantile). The importance of the variance is mainly due to the role played by this concept in limit theorems. Roughly speaking, one may say that if the expectation and variance of the sum of a large number of random variables are known, it is possible to describe completely the distribution law of this sum: It is (approximately) normal, with corresponding parameters (cf. Normal distribution). Thus, the most important properties of the variance are connected with the expression for the variance $\Var(X_1+\cdots+X_n)$ of the sum of random variables $X_1,\dots, X_n$:
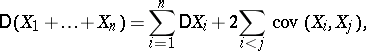 |
where
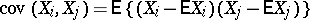 |
denotes the covariance of the random variables 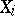 and
and 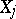 . If the random variables
. If the random variables 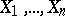 are pairwise independent, then
are pairwise independent, then 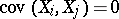 . Accordingly, the equation
. Accordingly, the equation
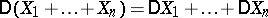 | (2) |
is valid for pairwise independent random variables. The converse proposition is not valid: (2) does not entail independence. Nevertheless, the utilization of (2) is usually based on the independence of the random variables. Strictly speaking, a sufficient condition for the validity of (2) is that 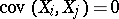 , i.e. the random variables
, i.e. the random variables 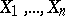 need to be pairwise uncorrelated.
need to be pairwise uncorrelated.
The applications of the concept of the variance have had two directions of development. The first is in the limit theorems of probability theory. If, for a sequence of random variables 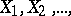 one has
one has 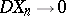 as
as 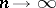 , then for any
, then for any 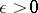 ,
,
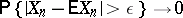 |
as 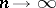 (cf. Chebyshev inequality in probability theory), i.e. if
(cf. Chebyshev inequality in probability theory), i.e. if  is large the random variable
is large the random variable 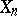 becomes practically identical with the non-random variable
becomes practically identical with the non-random variable 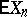 . The development of these concepts yields a proof of the law of large numbers, of the consistency of estimators (cf. Consistent estimator) in mathematical statistics, and also leads to other applications in which convergence in probability is established for random variables. Another application to limit theorems is connected with the concept of normalization. Normalization of a random variable
. The development of these concepts yields a proof of the law of large numbers, of the consistency of estimators (cf. Consistent estimator) in mathematical statistics, and also leads to other applications in which convergence in probability is established for random variables. Another application to limit theorems is connected with the concept of normalization. Normalization of a random variable 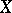 is effected by subtracting the expectation and dividing by the square root of the variance
is effected by subtracting the expectation and dividing by the square root of the variance 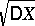 ; in other words, the variable
; in other words, the variable  is considered. Normalization of a sequence of random variables is usually necessary in order to obtain a convergent sequence of distribution laws, in particular, convergence to the normal law with parameters zero and one. The second direction consists in the application of the concept of the variance in mathematical statistics to sample processing. If a random variable is considered as the realization of a random experiment, an arbitrary change in the numerical scale converts the random variable
is considered. Normalization of a sequence of random variables is usually necessary in order to obtain a convergent sequence of distribution laws, in particular, convergence to the normal law with parameters zero and one. The second direction consists in the application of the concept of the variance in mathematical statistics to sample processing. If a random variable is considered as the realization of a random experiment, an arbitrary change in the numerical scale converts the random variable 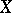 to
to , where
 is an arbitrary random number and
is an arbitrary random number and 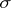 is a positive number. It is accordingly meaningful, in many cases, to consider not the one theoretical distribution law
is a positive number. It is accordingly meaningful, in many cases, to consider not the one theoretical distribution law 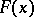 of the random variable
of the random variable 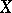 alone, but rather the type of the law, i.e. the family of distribution laws of the type $F((x-a)/\sigma)$, which is a function of at least two parameters
alone, but rather the type of the law, i.e. the family of distribution laws of the type $F((x-a)/\sigma)$, which is a function of at least two parameters  and
and 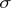 . If
. If 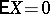 ,
,  , then
, then 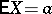 and
and 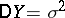 . Accordingly, the meaning of the parameters in the theoretical law is
. Accordingly, the meaning of the parameters in the theoretical law is 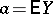 and
and 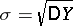 . This makes it possible to determine these parameters by sampling.
. This makes it possible to determine these parameters by sampling.
References
| [G] | B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian) |
| [F] | W. Feller, "An introduction to probability theory and its applications", 1–2, Wiley (1957–1971) |
| [C] | H. Cramér, "Mathematical methods of statistics", Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
Comments
Dispersion is usually termed variance in English, and one accordingly uses 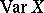 instead of
instead of 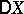 .
.
Variance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variance&oldid=29498