Vanishing cycle
Let  be an
be an  -dimensional complex manifold with boundary,
-dimensional complex manifold with boundary,  a Riemann surface and
a Riemann surface and  a proper holomorphic mapping which has no critical points on the boundary of
a proper holomorphic mapping which has no critical points on the boundary of  and only non-degenerate critical points on the interior with distinct critical values. Let
and only non-degenerate critical points on the interior with distinct critical values. Let  be a path on
be a path on  such that
such that  is a critical value of
is a critical value of  but
but  is a regular value for
is a regular value for  . For
. For  , write
, write  . The group
. The group  is then infinite cyclic. An
is then infinite cyclic. An  -chain
-chain  on
on  generating it is called a Lefschetz thimble and its boundary
generating it is called a Lefschetz thimble and its boundary  a (Lefschetz) vanishing cycle [a1]. It is uniquely determined by
a (Lefschetz) vanishing cycle [a1]. It is uniquely determined by 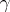 up to sign. Two cases are of particular importance: the case of a Lefschetz pencil of hyperplane sections of a projective variety (see Monodromy transformation) and of semi-universal deformations of isolated complete intersection singularities [a2], [a3]. In the latter case, one first restricts the semi-universal deformation to a smooth curve which intersects the discriminant transversely. Suitable choices of paths connecting a regular value
up to sign. Two cases are of particular importance: the case of a Lefschetz pencil of hyperplane sections of a projective variety (see Monodromy transformation) and of semi-universal deformations of isolated complete intersection singularities [a2], [a3]. In the latter case, one first restricts the semi-universal deformation to a smooth curve which intersects the discriminant transversely. Suitable choices of paths connecting a regular value 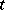 with the critical values lead to (strongly or weakly) distinguished bases of the vanishing homology group
with the critical values lead to (strongly or weakly) distinguished bases of the vanishing homology group  .
.
If  is a holomorphic function on a complex space
is a holomorphic function on a complex space  and
and  is a constructible sheaf complex on
is a constructible sheaf complex on  , one obtains a constructible sheaf complex
, one obtains a constructible sheaf complex  on
on 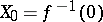 in the following way. Let
in the following way. Let  be a universal covering and let
be a universal covering and let  ,
,  be the natural mappings. Then
be the natural mappings. Then 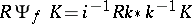 . The functor
. The functor  is called the nearby cycle functor. There is a distinguished triangle
is called the nearby cycle functor. There is a distinguished triangle
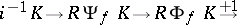 |
in the derived category  . Here
. Here  is the vanishing cycle functor associated to
is the vanishing cycle functor associated to  [a4].
[a4].
If the sheaf complex  is perverse, the same holds for
is perverse, the same holds for  and
and  . If
. If  is a complex manifold, by the Riemann–Hilbert correspondence one has vanishing and nearby cycle functors
is a complex manifold, by the Riemann–Hilbert correspondence one has vanishing and nearby cycle functors  and
and  in the category of regular holonomic
in the category of regular holonomic  -modules [a5], [a6] (see also
-modules [a5], [a6] (see also  -module; Derived category). They play a crucial role in the theory of mixed Hodge modules [a7].
-module; Derived category). They play a crucial role in the theory of mixed Hodge modules [a7].
References
| [a1] | S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) MR0033557 MR1520618 |
| [a2] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 2 , Birkhäuser (1988) (Translated from Russian) MR966191 Zbl 0659.58002 |
| [a3] | W. Ebeling, "The monodromy groups of isolated singularities of complete intersections" , Lect. notes in math. , 1293 , Springer (1987) MR0923114 Zbl 0683.32001 |
| [a4] | P. Deligne (ed.) N.M. Katz (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) MR0354657 |
| [a5] | B. Malgrange, "Le polynôme de I.N. Bernstein d'une singularité isolée" , Lect. notes in math. , 459 , Springer (1976) MR0409883 |
| [a6] | Z. Mebkhout, "Systèmes différentiels. Le formalisme des six opérations de Grothendieck pour les 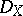 -modules cohérents" , Hermann (1989) MR0907933 -modules cohérents" , Hermann (1989) MR0907933 |
| [a7] | M. Saito, "Mixed Hodge modules" Publ. R.I.M.S. Kyoto Univ. , 26 (1990) pp. 221–333 MR1047741 MR1047415 Zbl 0727.14004 Zbl 0726.14007 |
Vanishing cycle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vanishing_cycle&oldid=24588