Difference between revisions of "Vanishing cycle"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | v0960701.png | ||
| + | $#A+1 = 44 n = 1 | ||
| + | $#C+1 = 44 : ~/encyclopedia/old_files/data/V096/V.0906070 Vanishing cycle | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ X $ | |
| + | be an $ n $- | ||
| + | dimensional complex manifold with boundary, $ U $ | ||
| + | a Riemann surface and $ f : X \rightarrow U $ | ||
| + | a proper holomorphic mapping which has no critical points on the boundary of $ X $ | ||
| + | and only non-degenerate critical points on the interior with distinct critical values. Let $ \gamma $ | ||
| + | be a path on $ U $ | ||
| + | such that $ \gamma ( 0) $ | ||
| + | is a critical value of $ f $ | ||
| + | but $ \gamma ( \tau ) $ | ||
| + | is a regular value for $ \tau \in ( 0, 1] $. | ||
| + | For $ V\subset [ 0, 1] $, | ||
| + | write $ X _ {V} = \{ {( x, \tau ) \in X \times V } : {f( x) = \gamma ( \tau ) } \} $. | ||
| + | The group $ H _ {n} ( X _ {[ 0,1] } , X _ {1} ) $ | ||
| + | is then infinite cyclic. An $ n $- | ||
| + | chain $ \Delta $ | ||
| + | on $ X _ {[ 0,1] } $ | ||
| + | generating it is called a Lefschetz thimble and its boundary $ \delta = \partial \Delta \in H _ {n- 1 } ( X _ {1} ) $ | ||
| + | a (Lefschetz) vanishing cycle [[#References|[a1]]]. It is uniquely determined by $ \gamma $ | ||
| + | up to sign. Two cases are of particular importance: the case of a Lefschetz pencil of hyperplane sections of a projective variety (see [[Monodromy transformation|Monodromy transformation]]) and of semi-universal deformations of isolated complete intersection singularities [[#References|[a2]]], [[#References|[a3]]]. In the latter case, one first restricts the semi-universal deformation to a smooth curve which intersects the discriminant transversely. Suitable choices of paths connecting a regular value $ t $ | ||
| + | with the critical values lead to (strongly or weakly) distinguished bases of the vanishing homology group $ H _ {n- 1 } ( X _ {t} ) $. | ||
| − | in the | + | If $ f : X \rightarrow \mathbf C $ |
| + | is a holomorphic function on a complex space $ X $ | ||
| + | and $ K $ | ||
| + | is a constructible sheaf complex on $ X $, | ||
| + | one obtains a constructible sheaf complex $ R \Psi _ {f} ( K) $ | ||
| + | on $ X _ {0} = f ^ { - 1 } ( 0) $ | ||
| + | in the following way. Let $ H \rightarrow \mathbf C ^ {*} $ | ||
| + | be a universal covering and let $ k : X \times _ {\mathbf C ^ {*} } H \rightarrow X $, | ||
| + | $ i : X _ {0} \rightarrow X $ | ||
| + | be the natural mappings. Then $ R \Psi _ {f} K = i ^ {- 1 } Rk _ {*} k ^ {- 1 } K $. | ||
| + | The functor $ R \Psi _ {f} $ | ||
| + | is called the nearby cycle functor. There is a distinguished triangle | ||
| − | If the sheaf complex | + | $$ |
| + | i ^ {- 1 } K \rightarrow R \Psi _ {f} K \rightarrow R \Phi _ {f} K \mathop \rightarrow \limits ^ { {+ 1 }} | ||
| + | $$ | ||
| + | |||
| + | in the derived category $ D _ {c} ^ {b} ( X _ {0} ) $. | ||
| + | Here $ R \Phi _ {f} $ | ||
| + | is the vanishing cycle functor associated to $ f $[[#References|[a4]]]. | ||
| + | |||
| + | If the sheaf complex $ K $ | ||
| + | is perverse, the same holds for $ R \Psi _ {f} K $ | ||
| + | and $ R \Phi _ {f} K $. | ||
| + | If $ X $ | ||
| + | is a complex manifold, by the Riemann–Hilbert correspondence one has vanishing and nearby cycle functors $ \phi _ {f} $ | ||
| + | and $ \psi _ {f} $ | ||
| + | in the category of regular holonomic $ D _ {X} $- | ||
| + | modules [[#References|[a5]]], [[#References|[a6]]] (see also [[D-module| $ D $- | ||
| + | module]]; [[Derived category|Derived category]]). They play a crucial role in the theory of mixed Hodge modules [[#References|[a7]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) {{MR|0033557}} {{MR|1520618}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''2''' , Birkhäuser (1988) (Translated from Russian) {{MR|966191}} {{ZBL|0659.58002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Ebeling, "The monodromy groups of isolated singularities of complete intersections" , ''Lect. notes in math.'' , '''1293''' , Springer (1987) {{MR|0923114}} {{ZBL|0683.32001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne (ed.) N.M. Katz (ed.) , ''Groupes de monodromie en géométrie algébrique. SGA 7.II'' , ''Lect. notes in math.'' , '''340''' , Springer (1973) {{MR|0354657}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Malgrange, "Le polynôme de I.N. Bernstein d'une singularité isolée" , ''Lect. notes in math.'' , '''459''' , Springer (1976) {{MR|0409883}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Z. Mebkhout, "Systèmes différentiels. Le formalisme des six opérations de Grothendieck pour les <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096070/v09607045.png" />-modules cohérents" , Hermann (1989) {{MR|0907933}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Saito, "Mixed Hodge modules" ''Publ. R.I.M.S. Kyoto Univ.'' , '''26''' (1990) pp. 221–333 {{MR|1047741}} {{MR|1047415}} {{ZBL|0727.14004}} {{ZBL|0726.14007}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) {{MR|0033557}} {{MR|1520618}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''2''' , Birkhäuser (1988) (Translated from Russian) {{MR|966191}} {{ZBL|0659.58002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Ebeling, "The monodromy groups of isolated singularities of complete intersections" , ''Lect. notes in math.'' , '''1293''' , Springer (1987) {{MR|0923114}} {{ZBL|0683.32001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne (ed.) N.M. Katz (ed.) , ''Groupes de monodromie en géométrie algébrique. SGA 7.II'' , ''Lect. notes in math.'' , '''340''' , Springer (1973) {{MR|0354657}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Malgrange, "Le polynôme de I.N. Bernstein d'une singularité isolée" , ''Lect. notes in math.'' , '''459''' , Springer (1976) {{MR|0409883}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Z. Mebkhout, "Systèmes différentiels. Le formalisme des six opérations de Grothendieck pour les <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096070/v09607045.png" />-modules cohérents" , Hermann (1989) {{MR|0907933}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Saito, "Mixed Hodge modules" ''Publ. R.I.M.S. Kyoto Univ.'' , '''26''' (1990) pp. 221–333 {{MR|1047741}} {{MR|1047415}} {{ZBL|0727.14004}} {{ZBL|0726.14007}} </TD></TR></table> | ||
Latest revision as of 08:27, 6 June 2020
Let $ X $
be an $ n $-
dimensional complex manifold with boundary, $ U $
a Riemann surface and $ f : X \rightarrow U $
a proper holomorphic mapping which has no critical points on the boundary of $ X $
and only non-degenerate critical points on the interior with distinct critical values. Let $ \gamma $
be a path on $ U $
such that $ \gamma ( 0) $
is a critical value of $ f $
but $ \gamma ( \tau ) $
is a regular value for $ \tau \in ( 0, 1] $.
For $ V\subset [ 0, 1] $,
write $ X _ {V} = \{ {( x, \tau ) \in X \times V } : {f( x) = \gamma ( \tau ) } \} $.
The group $ H _ {n} ( X _ {[ 0,1] } , X _ {1} ) $
is then infinite cyclic. An $ n $-
chain $ \Delta $
on $ X _ {[ 0,1] } $
generating it is called a Lefschetz thimble and its boundary $ \delta = \partial \Delta \in H _ {n- 1 } ( X _ {1} ) $
a (Lefschetz) vanishing cycle [a1]. It is uniquely determined by $ \gamma $
up to sign. Two cases are of particular importance: the case of a Lefschetz pencil of hyperplane sections of a projective variety (see Monodromy transformation) and of semi-universal deformations of isolated complete intersection singularities [a2], [a3]. In the latter case, one first restricts the semi-universal deformation to a smooth curve which intersects the discriminant transversely. Suitable choices of paths connecting a regular value $ t $
with the critical values lead to (strongly or weakly) distinguished bases of the vanishing homology group $ H _ {n- 1 } ( X _ {t} ) $.
If $ f : X \rightarrow \mathbf C $ is a holomorphic function on a complex space $ X $ and $ K $ is a constructible sheaf complex on $ X $, one obtains a constructible sheaf complex $ R \Psi _ {f} ( K) $ on $ X _ {0} = f ^ { - 1 } ( 0) $ in the following way. Let $ H \rightarrow \mathbf C ^ {*} $ be a universal covering and let $ k : X \times _ {\mathbf C ^ {*} } H \rightarrow X $, $ i : X _ {0} \rightarrow X $ be the natural mappings. Then $ R \Psi _ {f} K = i ^ {- 1 } Rk _ {*} k ^ {- 1 } K $. The functor $ R \Psi _ {f} $ is called the nearby cycle functor. There is a distinguished triangle
$$ i ^ {- 1 } K \rightarrow R \Psi _ {f} K \rightarrow R \Phi _ {f} K \mathop \rightarrow \limits ^ { {+ 1 }} $$
in the derived category $ D _ {c} ^ {b} ( X _ {0} ) $. Here $ R \Phi _ {f} $ is the vanishing cycle functor associated to $ f $[a4].
If the sheaf complex $ K $ is perverse, the same holds for $ R \Psi _ {f} K $ and $ R \Phi _ {f} K $. If $ X $ is a complex manifold, by the Riemann–Hilbert correspondence one has vanishing and nearby cycle functors $ \phi _ {f} $ and $ \psi _ {f} $ in the category of regular holonomic $ D _ {X} $- modules [a5], [a6] (see also $ D $- module; Derived category). They play a crucial role in the theory of mixed Hodge modules [a7].
References
| [a1] | S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) MR0033557 MR1520618 |
| [a2] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 2 , Birkhäuser (1988) (Translated from Russian) MR966191 Zbl 0659.58002 |
| [a3] | W. Ebeling, "The monodromy groups of isolated singularities of complete intersections" , Lect. notes in math. , 1293 , Springer (1987) MR0923114 Zbl 0683.32001 |
| [a4] | P. Deligne (ed.) N.M. Katz (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) MR0354657 |
| [a5] | B. Malgrange, "Le polynôme de I.N. Bernstein d'une singularité isolée" , Lect. notes in math. , 459 , Springer (1976) MR0409883 |
| [a6] | Z. Mebkhout, "Systèmes différentiels. Le formalisme des six opérations de Grothendieck pour les 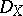 -modules cohérents" , Hermann (1989) MR0907933 -modules cohérents" , Hermann (1989) MR0907933 |
| [a7] | M. Saito, "Mixed Hodge modules" Publ. R.I.M.S. Kyoto Univ. , 26 (1990) pp. 221–333 MR1047741 MR1047415 Zbl 0727.14004 Zbl 0726.14007 |
Vanishing cycle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vanishing_cycle&oldid=24588