Difference between revisions of "User:Nikita2/sandbox"
m (→AsymptotePlay) |
|||
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A mapping $\varphi:D\to D'$ possesses Luzin's $\mathcal N$-property if the image of every set of measure zero is a set of measure zero. A mapping $\varphi$ possesses Luzin's $\mathcal N{}^{-1}$-property if the preimage of every set of measure zero is a set of measure zero. | |
| − | + | ''Briefly'' | |
| + | \begin{equation*} | ||
| + | \mathcal N\text{-property:}\quad \Sigma\subset D, |\Sigma| = 0 \Rightarrow |\varphi(\Sigma)|=0, | ||
| + | \end{equation*} | ||
| + | \begin{equation*} | ||
| + | \mathcal N{}^{-1}\text{-property:} \quad M \subset D, |M| = 0 \Rightarrow |\varphi^{-1}(M)|=0. | ||
| + | \end{equation*} | ||
| − | + | ||
| + | ====$\mathcal N$-property of a function $f$ on an interval $[a,b]$==== | ||
| + | |||
| + | Let $f:[a,b]\to \mathbb R$ be a measurable function. In this case the definition is following: | ||
| + | ''For any set $E\subset[a,b]$ of measure zero ($|E|=0$), the image of this set, $f(E)$, also has measure zero.'' | ||
| + | It was introduced by N.N. Luzin in 1915 (see [[#References|[1]]]). The following assertions hold. | ||
| + | # A function $f\not\equiv \operatorname{const}$ on $[a,b]$ such that $f'(x)=0 $ almost-everywhere on $[a,b]$ (see for example [[Cantor_ternary_function|Cantor ternary function]]) does not have the Luzin $\mathcal N$-property. | ||
| + | # If $f$ does not have the Luzin $\mathcal N$-property, then on $[a,b]$ there is a [[Perfect set|perfect set]] $P$ of measure zero such that $|f(P)|>0$. | ||
| + | # An [[Absolutely_continuous_function#Absolute_continuity_of_a_function|absolutely continuous function]] has the Luzin $\mathcal N$-property. | ||
| + | # If $f$ has the Luzin $\mathcal N$-property and has [[Function_of_bounded_variation#Classical_definition|bounded variation]] on $[a,b]$ (as well as being continuous on $[a,b]$), then $f$ is absolutely continuous on $[a,b]$ (the Banach–Zaretskii theorem). | ||
| + | # If $f$ does not decrease on $[a,b]$ and $f'$ is finite on $[a,b]$, then $f$ has the Luzin $\mathcal N$-property. | ||
| + | # In order that $f(E)$ be measurable for every measurable set $E\subset[a,b]$ it is necessary and sufficient that $f$ have the Luzin $\mathcal N$-property on $[a,b]$. | ||
| + | # A function $f$ that has the Luzin $\mathcal N$-property has a derivative $f'$ on the set for which any non-empty [[Portion|portion]] of it has positive measure. | ||
| + | # For any perfect nowhere-dense set $P\subset[a,b]$ there is a function $f$ having the Luzin $\mathcal N$-property on $[a,b]$ and such that $f'$ does not exist at any point of $P$. | ||
The concept of Luzin's <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l061/l061050/l06105044.png" />-property can be generalized to functions of several variables and functions of a more general nature, defined on measure spaces. | The concept of Luzin's <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l061/l061050/l06105044.png" />-property can be generalized to functions of several variables and functions of a more general nature, defined on measure spaces. | ||
| Line 48: | Line 60: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===AsymptotePlay=== | ||
<asy> | <asy> | ||
import graph; | import graph; | ||
| − | |||
| − | |||
| − | + | size(400,200,IgnoreAspect); | |
| − | + | ||
| − | + | int n=2; | |
| − | |||
| − | |||
| − | + | real[] a=new real[n]; | |
| − | + | real[] x=new real[n]; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | //real[] x=sequence(n); | ||
| − | + | string[] month={"Jan","February","March","April","May","Jun","Jul","Aug","Sep","Oct","Nov","Dec"}; | |
| − | |||
| − | |||
| − | |||
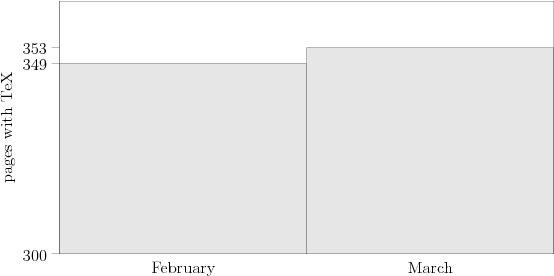
| − | + | a[0]=349; //February | |
| − | + | a[1]=353; //March | |
| − | + | a[2]=363; //April | |
| − | + | a[3]=353; //May | |
| + | a[4]=353; //June | ||
| − | + | void mbox(real m, real c) | |
| − | + | { | |
| − | + | path g=box((m-0.5,0),(m+0.5,c)); | |
| − | + | filldraw(g,lightgrey); | |
| − | + | } | |
| + | for(int i=0; i<n;++i){x[i]=i+0.5;} | ||
| + | for(int i=0; i < n; ++i){ mbox(i,a[i]);} | ||
| + | //draw((-0.5,300)--(n-0.5,300)); | ||
| + | draw(box((-0.5,300),(n-0.5,a[n]+2))); | ||
| + | limits((-0.5,300),(n-0.5,a[n]+2),Crop); | ||
| + | |||
| + | xaxis(xmin=0,Bottom,LeftTicks(Step=1,new string(real y) {return month[round(y+1 % 12)];})); | ||
| + | yaxis("pages with TeX",Left,LeftTicks(DefaultFormat, new real[] {300,a[0],a[1]})); | ||
</asy> | </asy> | ||
| + | |||
| + | ===FigurePlay=== | ||
| + | <span id="Fig1", bg="black"> | ||
| + | [[File:Cochleoid-1.png| right| frame| Figure 1. The cochleoid ([[Media:Cochleoid-1.pdf|pdf]]) ]] | ||
| + | </span> | ||
Latest revision as of 07:08, 3 March 2013
A mapping $\varphi:D\to D'$ possesses Luzin's $\mathcal N$-property if the image of every set of measure zero is a set of measure zero. A mapping $\varphi$ possesses Luzin's $\mathcal N{}^{-1}$-property if the preimage of every set of measure zero is a set of measure zero.
Briefly \begin{equation*} \mathcal N\text{-property:}\quad \Sigma\subset D, |\Sigma| = 0 \Rightarrow |\varphi(\Sigma)|=0, \end{equation*} \begin{equation*} \mathcal N{}^{-1}\text{-property:} \quad M \subset D, |M| = 0 \Rightarrow |\varphi^{-1}(M)|=0. \end{equation*}
$\mathcal N$-property of a function $f$ on an interval $[a,b]$
Let $f:[a,b]\to \mathbb R$ be a measurable function. In this case the definition is following: For any set $E\subset[a,b]$ of measure zero ($|E|=0$), the image of this set, $f(E)$, also has measure zero. It was introduced by N.N. Luzin in 1915 (see [1]). The following assertions hold.
- A function $f\not\equiv \operatorname{const}$ on $[a,b]$ such that $f'(x)=0 $ almost-everywhere on $[a,b]$ (see for example Cantor ternary function) does not have the Luzin $\mathcal N$-property.
- If $f$ does not have the Luzin $\mathcal N$-property, then on $[a,b]$ there is a perfect set $P$ of measure zero such that $|f(P)|>0$.
- An absolutely continuous function has the Luzin $\mathcal N$-property.
- If $f$ has the Luzin $\mathcal N$-property and has bounded variation on $[a,b]$ (as well as being continuous on $[a,b]$), then $f$ is absolutely continuous on $[a,b]$ (the Banach–Zaretskii theorem).
- If $f$ does not decrease on $[a,b]$ and $f'$ is finite on $[a,b]$, then $f$ has the Luzin $\mathcal N$-property.
- In order that $f(E)$ be measurable for every measurable set $E\subset[a,b]$ it is necessary and sufficient that $f$ have the Luzin $\mathcal N$-property on $[a,b]$.
- A function $f$ that has the Luzin $\mathcal N$-property has a derivative $f'$ on the set for which any non-empty portion of it has positive measure.
- For any perfect nowhere-dense set $P\subset[a,b]$ there is a function $f$ having the Luzin $\mathcal N$-property on $[a,b]$ and such that $f'$ does not exist at any point of $P$.
The concept of Luzin's 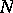 -property can be generalized to functions of several variables and functions of a more general nature, defined on measure spaces.
-property can be generalized to functions of several variables and functions of a more general nature, defined on measure spaces.
References
| [1] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
Comments
There is another property intimately related to the Luzin 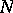 -property. A function
-property. A function 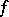 continuous on an interval
continuous on an interval 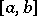 has the Banach
has the Banach 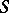 -property if for all Lebesgue-measurable sets
-property if for all Lebesgue-measurable sets 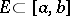 and all
and all 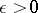 is a
is a 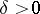 such that
such that
 |
This is clearly stronger than the 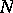 -property. S. Banach proved that a function
-property. S. Banach proved that a function 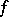 has the
has the 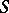 -property (respectively, the
-property (respectively, the 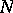 -property) if and only if (respectively, only if — see below for the missing "if" ) the inverse image
-property) if and only if (respectively, only if — see below for the missing "if" ) the inverse image 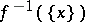 is finite (respectively, is at most countable) for almost-all
is finite (respectively, is at most countable) for almost-all  in
in  . For classical results on the
. For classical results on the 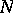 - and
- and  -properties, see [a3].
-properties, see [a3].
Recently a powerful extension of these results has been given by G. Mokobodzki (cf. [a1], [a2]), allowing one to prove deep results in potential theory. Let  and
and 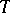 be two compact metrizable spaces,
be two compact metrizable spaces,  being equipped with a probability measure
being equipped with a probability measure  . Let
. Let 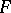 be a Borel subset of
be a Borel subset of  and, for any Borel subset
and, for any Borel subset  of
of  , define the subset
, define the subset 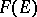 of
of 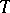 by
by  (if
(if 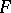 is the graph of a mapping
is the graph of a mapping 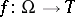 , then
, then 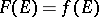 ). The set
). The set 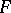 is said to have the property (N) (respectively, the property (S)) if there exists a measure
is said to have the property (N) (respectively, the property (S)) if there exists a measure 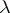 on
on 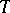 (here depending on
(here depending on 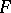 ) such that for all
) such that for all 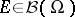 ,
,
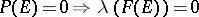 |
(respectively, for all 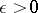 there is a
there is a 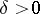 such that for all
such that for all  one has
one has
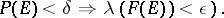 |
Now 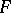 has the property (N) (respectively, the property (S)) if and only if the section
has the property (N) (respectively, the property (S)) if and only if the section 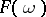 of
of  is at most countable (respectively, is finite) for almost-all
is at most countable (respectively, is finite) for almost-all 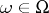 .
.
References
| [a1] | C. Dellacherie, D. Feyel, G. Mokobodzki, "Intégrales de capacités fortement sous-additives" , Sem. Probab. Strasbourg XVI , Lect. notes in math. , 920 , Springer (1982) pp. 8–28 MR0658670 Zbl 0496.60076 |
| [a2] | A. Louveau, "Minceur et continuité séquentielle des sous-mesures analytiques fortement sous-additives" , Sem. Initiation à l'Analyse , 66 , Univ. P. et M. Curie (1983–1984) Zbl 0587.28003 |
| [a3] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) MR0167578 Zbl 1196.28001 Zbl 0017.30004 Zbl 63.0183.05 |
| [a4] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202 |
AsymptotePlay
FigurePlay

Nikita2/sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nikita2/sandbox&oldid=29109