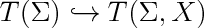|
|
| (280 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | $\newcommand{\Om}{\Omega}
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| − | \newcommand{\A}{\mathcal A}
| |
| − | \newcommand{\B}{\mathcal B}
| |
| − | \newcommand{\M}{\mathcal M} $
| |
| − | The term '''"universally measurable"''' may be applied to
| |
| − | * a [[measurable space]];
| |
| − | * a subset of a measurable space;
| |
| − | * a [[metric space]].
| |
| | | | |
| − | Let $(X,\A)$ be a measurable space. A ''subset'' $A\subset X$ is called ''universally measurable'' if it is $\mu$-measurable for every finite measure $\mu$ on $(X,\A)$. In other words: $\mu_*(A)=\mu^*(A)$ where $\mu_*,\mu^*$ are the inner and outer measures for $\mu$, that is,
| + | ====Notes==== |
| − | : $ \mu_*(A) = \max\{\mu(B):B\in\A,B\subset A\}\,,\quad
| + | <references /> |
| − | \mu^*(A) = \min\{\mu(B):B\in\A,B\supset A\}\,.$
| |
| − | (See {{Cite|S|p. 170}}.)
| |
| | | | |
| − | A separable ''metric space'' is called ''universally measurable'' if it is a universally measurable subset (as defined above) of its [[Metric space#completion|completion]]. Here the completion, endowed with the [[Measurable space#Borel sets|Borel σ-algebra]], is treated as a measurable space. (See {{Cite|S|p. 170}}, {{Cite|D|Sect. 11.5}}.)
| + | ------------------------------------------- |
| | | | |
| − | A ''measurable space'' is called ''universally measurable'' if it is [[Measurable space#isomorphic|isomorphic]] to some universally measurable metric space (as defined above) with the Borel σ-algebra. (See {{Cite|S|p. 171}}.)
| |
| | | | |
| − | '''Theorem 1''' (Shortt). A [[Measurable space#countably generated|countably generated]] [[Measurable space#separated|separated]] measurable space $(X,\A)$ is universally measurable if and only if for every finite measure $\mu$ on $(X,\A)$ there exists a subset $A\in\A$ of full measure (that is, $\mu(X\setminus A)=0$) such that $A$ (treated as a [[Measurable space#subspace|subspace]]) is itself a [[standard Borel space]]. ({{Cite|S|Lemma 4}})
| + | {| |
| | + | | A || B || C |
| | + | |- |
| | + | | X || Y || Z |
| | + | |} |
| | + | |
| | + | |
| | + | |
| | + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | + | |
| | + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | + | |
| | + | <asy> |
| | + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | + | |
| | + | <asy> |
| | + | size(220,220); |
| | + | |
| | + | import math; |
| | | | |
| − | '''Theorem 2''' (Shortt). The following two conditions on a separable metric space are equivalent:
| + | int kmax=40; |
| − | :(a) it is a universally measurable metric space;
| |
| − | :(b) the corresponding measurable space (with the Borel σ-algebra) is universally measurable.
| |
| | | | |
| − | Evidently, (a) implies (b); surprisingly, also (b) implies (a), which involves a Borel isomorphism (rather than isometry or homeomorphism) between two metric spaces.
| + | guide g; |
| | + | for (int k=-kmax; k<=kmax; ++k) { |
| | + | real phi = 0.2*k*pi; |
| | + | real rho = 1; |
| | + | if (k!=0) { |
| | + | rho = sin(phi)/phi; |
| | + | } |
| | + | pair z=rho*expi(phi); |
| | + | g=g..z; |
| | + | } |
| | + | |
| | + | draw (g); |
| | | | |
| − | ====References====
| + | defaultpen(0.75); |
| | + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| | + | dot ( (1,0) ); |
| | + | label ( "$a$", (1,0), NE ); |
| | | | |
| − | {|
| + | </asy> |
| − | |valign="top"|{{Ref|S}}|| Rae M. Shortt, "Universally measurable spaces: an invariance theorem and diverse characterizations", ''Fundamenta Mathematicae'' '''121''' (1984), 169–176. {{MR|0765332}} {{ZBL|0573.28018}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|N}}|| Togo Nishiura, "Absolute measurable spaces", Cambridge (2008). {{MR|}} {{ZBL|0992.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|P}}|| David Pollard, "A user's guide to measure theoretic probability", Cambridge (2002). {{MR|1873379}} {{ZBL|0992.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|K}}|| Alexander S. Kechris, "Classical descriptive set theory", Springer-Verlag (1995). {{MR|1321597}} {{ZBL|0819.04002}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|BK}}|| Howard Becker and Alexander S. Kechris, "The descriptive set theory of Polish group actions", Cambridge (1996). {{MR|1425877}} {{ZBL|0949.54052}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|D}}|| Richard M. Dudley, "Real analysis and probability", Wadsworth&Brooks/Cole (1989). {{MR|0982264}} {{ZBL|0686.60001}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|M}}|| George W. Mackey, "Borel structure in groups and their duals", ''Trans. Amer. Math. Soc.'' '''85''' (1957), 134–165. {{MR|0089999}} {{ZBL|0082.11201}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|H}}|| Paul R. Halmos, "Measure theory", v. Nostrand (1950). {{MR|0033869}} {{ZBL|0040.16802}}
| |
| − | |-
| |
| − | |valign="top"|{{Ref|R}}|| Walter Rudin, "Principles of mathematical analysis", McGraw-Hill (1953). {{MR|0055409}} {{ZBL|0052.05301}}
| |
| − | |}
| |