Difference between revisions of "Upper-and-lower-functions method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | u0958201.png | ||
| + | $#A+1 = 46 n = 1 | ||
| + | $#C+1 = 46 : ~/encyclopedia/old_files/data/U095/U.0905820 Upper\AAhand\AAhlower\AAhfunctions method | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A method for demonstrating the existence of solutions of boundary value problems for differential equations. The idea of this method applied to ordinary differential equations was discussed in the work of G. Peano (1880). For the case of the [[Dirichlet problem|Dirichlet problem]] and for the case of the [[Laplace equation|Laplace equation]] the idea occurs in H. Poincaré's [[Balayage method|balayage method]]. O. Perron [[#References|[1]]] was the first to give a full exposition of the method of upper and lower functions for this last case. | A method for demonstrating the existence of solutions of boundary value problems for differential equations. The idea of this method applied to ordinary differential equations was discussed in the work of G. Peano (1880). For the case of the [[Dirichlet problem|Dirichlet problem]] and for the case of the [[Laplace equation|Laplace equation]] the idea occurs in H. Poincaré's [[Balayage method|balayage method]]. O. Perron [[#References|[1]]] was the first to give a full exposition of the method of upper and lower functions for this last case. | ||
| − | Let the Dirichlet problem be posed in a region | + | Let the Dirichlet problem be posed in a region $ G $ |
| + | of the space $ \mathbf R ^ {n} $, | ||
| + | $ n \geq 2 $, | ||
| + | for a linear, homogeneous, elliptic second-order equation with continuous coefficients, | ||
| − | + | $$ \tag{1 } | |
| + | Lu \equiv \sum _ { i,j= } 1 ^ { n } | ||
| + | a _ {ij} | ||
| + | \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } | ||
| + | + | ||
| + | \sum _ { i= } 1 ^ { n } | ||
| + | b _ {i} | ||
| + | \frac{\partial u }{\partial x _ {i} } | ||
| + | + | ||
| + | cu = 0, | ||
| + | $$ | ||
| − | + | $$ | |
| + | c \leq 0,\ x \in G, | ||
| + | $$ | ||
with the boundary condition | with the boundary condition | ||
| − | + | $$ \tag{2 } | |
| + | u ( x) = f ( x),\ x \in \partial G. | ||
| + | $$ | ||
| − | In the method of upper and lower functions one introduces a generalization of superharmonic functions (respectively, of subharmonic functions), under the assumption that the problems (1) and (2) are locally solvable. A function | + | In the method of upper and lower functions one introduces a generalization of superharmonic functions (respectively, of subharmonic functions), under the assumption that the problems (1) and (2) are locally solvable. A function $ v $ |
| + | which is continuous in $ G $ | ||
| + | is said to be a generalized superharmonic function (respectively, a generalized subharmonic function) in $ G $ | ||
| + | if for any sufficiently small ball $ K $, | ||
| + | $ \overline{K}\; \subset G $, | ||
| + | the inequality $ ( v) _ {K} \leq v $( | ||
| + | respectively, $ ( v) _ {K} \geq v $) | ||
| + | is true. Here, $ ( v) _ {K} $ | ||
| + | is a continuous function in $ G $ | ||
| + | which is equal to $ v $ | ||
| + | outside $ K $ | ||
| + | and on its boundary and which satisfies equation (1) inside $ K $. | ||
| + | For a continuous function $ f $ | ||
| + | on the boundary $ \partial G $, | ||
| + | a generalized superharmonic (respectively, a subharmonic) function $ v $ | ||
| + | is said to be upper (respectively, lower) if for $ x \in \partial G $ | ||
| + | the inequality $ v( x) \geq f( x) $( | ||
| + | respectively, $ v( x) \leq f( x) $) | ||
| + | is true. | ||
| − | The classes | + | The classes $ \Phi ( G, f ) $ |
| + | and $ \Psi ( G, f ) $ | ||
| + | of all upper and lower functions, respectively, are non-empty, and if $ v \in \Phi ( G, f ) $ | ||
| + | and $ w \in \Psi ( G, f ) $, | ||
| + | then $ v \geq w $[[#References|[3]]]. A generalized solution of the Dirichlet problem is defined as the smallest envelope of the class $ \Phi ( G, f ) $ | ||
| + | or as the largest envelope of the class $ \Psi ( G, f ) $: | ||
| − | + | $$ \tag{3 } | |
| + | u ( x) = \inf \{ {v ( x) } : {v \in \Phi ( G, f ) } \} = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \sup \{ w ( x): w \in \Psi ( G, f ) \} ,\ x \in G. | ||
| + | $$ | ||
| − | If the boundary | + | If the boundary $ \partial G $ |
| + | permits a [[Barrier|barrier]] at each one of its points, then $ u( x) = f( x) $ | ||
| + | everywhere on $ \partial G $, | ||
| + | i.e. $ u $ | ||
| + | is a classical solution of the Dirichlet problem. In the general case the behaviour of the generalized solution (3) of the elliptic equation (1) at boundary points fully parallels the behaviour of the generalized solution of the Laplace problem (cf. [[Perron method|Perron method]]). | ||
The method of upper and lower functions is also employed in the study of the first boundary value problem for linear homogeneous parabolic second-order equations of the form | The method of upper and lower functions is also employed in the study of the first boundary value problem for linear homogeneous parabolic second-order equations of the form | ||
| − | + | $$ | |
| + | Lu - | ||
| + | \frac{\partial u }{\partial t } | ||
| + | = 0,\ \ | ||
| + | ( x, t) \in G \times [ 0, T], | ||
| + | $$ | ||
with the initial condition | with the initial condition | ||
| − | + | $$ | |
| + | u ( x, 0) = f ( x, 0),\ \ | ||
| + | x \in G, | ||
| + | $$ | ||
and boundary condition | and boundary condition | ||
| − | + | $$ | |
| + | u ( x, t) = f ( x, t),\ \ | ||
| + | ( x, t) \in \partial G \times [ 0, T]. | ||
| + | $$ | ||
In this case superparabolic (subparabolic) functions, with properties analogous to those of generalized superharmonic (subharmonic) functions, are introduced [[#References|[4]]]. | In this case superparabolic (subparabolic) functions, with properties analogous to those of generalized superharmonic (subharmonic) functions, are introduced [[#References|[4]]]. | ||
| Line 37: | Line 109: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Perron, "Eine neue Behandlung der ersten Randwertaufgabe für <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095820/u09582041.png" />" ''Math. Z.'' , '''18''' (1923) pp. 42–54</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.I. Smirnov, "A course of higher mathematics" , '''4''' , Addison-Wesley (1964) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Perron, "Eine neue Behandlung der ersten Randwertaufgabe für <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095820/u09582041.png" />" ''Math. Z.'' , '''18''' (1923) pp. 42–54</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.I. Smirnov, "A course of higher mathematics" , '''4''' , Addison-Wesley (1964) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | In axiomatic potential theory, this method is usually called the Perron–Wiener–Brelot method. In its general form, this method defines the upper solution of the Dirichlet problem, for any open set | + | In axiomatic potential theory, this method is usually called the Perron–Wiener–Brelot method. In its general form, this method defines the upper solution of the Dirichlet problem, for any open set $ \Omega $ |
| + | satisfying the minimum principle and any numerical boundary function $ f $, | ||
| + | as the greatest lower bound of all upper functions: the lower-bounded hyperharmonic functions $ u $ | ||
| + | on $ \Omega $ | ||
| + | such that $ \lim\limits \inf u \geq f $ | ||
| + | on the boundary and $ u \geq 0 $ | ||
| + | outside some compact set. The lower solution is defined in a dual way. The Dirichlet problem admits a generalized solution if the upper and lower solutions are equal and harmonic (i.e. satisfy the differential equation). In this case, the boundary function is said to be resolutive. See [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972)</TD></TR></table> | ||
Revision as of 08:27, 6 June 2020
A method for demonstrating the existence of solutions of boundary value problems for differential equations. The idea of this method applied to ordinary differential equations was discussed in the work of G. Peano (1880). For the case of the Dirichlet problem and for the case of the Laplace equation the idea occurs in H. Poincaré's balayage method. O. Perron [1] was the first to give a full exposition of the method of upper and lower functions for this last case.
Let the Dirichlet problem be posed in a region $ G $ of the space $ \mathbf R ^ {n} $, $ n \geq 2 $, for a linear, homogeneous, elliptic second-order equation with continuous coefficients,
$$ \tag{1 } Lu \equiv \sum _ { i,j= } 1 ^ { n } a _ {ij} \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } + \sum _ { i= } 1 ^ { n } b _ {i} \frac{\partial u }{\partial x _ {i} } + cu = 0, $$
$$ c \leq 0,\ x \in G, $$
with the boundary condition
$$ \tag{2 } u ( x) = f ( x),\ x \in \partial G. $$
In the method of upper and lower functions one introduces a generalization of superharmonic functions (respectively, of subharmonic functions), under the assumption that the problems (1) and (2) are locally solvable. A function $ v $ which is continuous in $ G $ is said to be a generalized superharmonic function (respectively, a generalized subharmonic function) in $ G $ if for any sufficiently small ball $ K $, $ \overline{K}\; \subset G $, the inequality $ ( v) _ {K} \leq v $( respectively, $ ( v) _ {K} \geq v $) is true. Here, $ ( v) _ {K} $ is a continuous function in $ G $ which is equal to $ v $ outside $ K $ and on its boundary and which satisfies equation (1) inside $ K $. For a continuous function $ f $ on the boundary $ \partial G $, a generalized superharmonic (respectively, a subharmonic) function $ v $ is said to be upper (respectively, lower) if for $ x \in \partial G $ the inequality $ v( x) \geq f( x) $( respectively, $ v( x) \leq f( x) $) is true.
The classes $ \Phi ( G, f ) $ and $ \Psi ( G, f ) $ of all upper and lower functions, respectively, are non-empty, and if $ v \in \Phi ( G, f ) $ and $ w \in \Psi ( G, f ) $, then $ v \geq w $[3]. A generalized solution of the Dirichlet problem is defined as the smallest envelope of the class $ \Phi ( G, f ) $ or as the largest envelope of the class $ \Psi ( G, f ) $:
$$ \tag{3 } u ( x) = \inf \{ {v ( x) } : {v \in \Phi ( G, f ) } \} = $$
$$ = \ \sup \{ w ( x): w \in \Psi ( G, f ) \} ,\ x \in G. $$
If the boundary $ \partial G $ permits a barrier at each one of its points, then $ u( x) = f( x) $ everywhere on $ \partial G $, i.e. $ u $ is a classical solution of the Dirichlet problem. In the general case the behaviour of the generalized solution (3) of the elliptic equation (1) at boundary points fully parallels the behaviour of the generalized solution of the Laplace problem (cf. Perron method).
The method of upper and lower functions is also employed in the study of the first boundary value problem for linear homogeneous parabolic second-order equations of the form
$$ Lu - \frac{\partial u }{\partial t } = 0,\ \ ( x, t) \in G \times [ 0, T], $$
with the initial condition
$$ u ( x, 0) = f ( x, 0),\ \ x \in G, $$
and boundary condition
$$ u ( x, t) = f ( x, t),\ \ ( x, t) \in \partial G \times [ 0, T]. $$
In this case superparabolic (subparabolic) functions, with properties analogous to those of generalized superharmonic (subharmonic) functions, are introduced [4].
References
| [1] | O. Perron, "Eine neue Behandlung der ersten Randwertaufgabe für 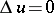 " Math. Z. , 18 (1923) pp. 42–54 " Math. Z. , 18 (1923) pp. 42–54 |
| [2] | I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian) |
| [3] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
Comments
In axiomatic potential theory, this method is usually called the Perron–Wiener–Brelot method. In its general form, this method defines the upper solution of the Dirichlet problem, for any open set $ \Omega $ satisfying the minimum principle and any numerical boundary function $ f $, as the greatest lower bound of all upper functions: the lower-bounded hyperharmonic functions $ u $ on $ \Omega $ such that $ \lim\limits \inf u \geq f $ on the boundary and $ u \geq 0 $ outside some compact set. The lower solution is defined in a dual way. The Dirichlet problem admits a generalized solution if the upper and lower solutions are equal and harmonic (i.e. satisfy the differential equation). In this case, the boundary function is said to be resolutive. See [a1].
References
| [a1] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
Upper-and-lower-functions method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Upper-and-lower-functions_method&oldid=17894