Ultimately periodic sequence
A sequence  over some set
over some set  satisfying the condition
satisfying the condition
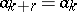 |
for all sufficiently large values of  and some
and some  is called ultimately periodic with period
is called ultimately periodic with period  ; if this condition actually holds for all
; if this condition actually holds for all  ,
,  is called periodic (with period
is called periodic (with period  ). The smallest number
). The smallest number  among all periods of
among all periods of  is called the least period of
is called the least period of  . The periods of
. The periods of  are precisely the multiples of
are precisely the multiples of 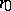 . Moreover, if
. Moreover, if  should be periodic for some period
should be periodic for some period  , it is actually periodic with period
, it is actually periodic with period  .
.
One may characterize the ultimately periodic sequences over some field  by associating an arbitrary sequence
by associating an arbitrary sequence 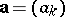 over
over  with the formal power series
with the formal power series
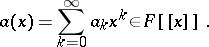 |
Then  is ultimately periodic with period
is ultimately periodic with period  if and only if
if and only if  is a polynomial over
is a polynomial over  . Any ultimately periodic sequence over a field is a shift register sequence. The converse is not true in general, as the Fibonacci sequence over the rationals shows (cf. Shift register sequence). However, the ultimately periodic sequences over a Galois field are precisely the shift register sequences. Periodic sequences (in particular, binary ones) with good correlation properties are important in engineering applications (cf. Correlation property for sequences).
. Any ultimately periodic sequence over a field is a shift register sequence. The converse is not true in general, as the Fibonacci sequence over the rationals shows (cf. Shift register sequence). However, the ultimately periodic sequences over a Galois field are precisely the shift register sequences. Periodic sequences (in particular, binary ones) with good correlation properties are important in engineering applications (cf. Correlation property for sequences).
References
| [a1] | D. Jungnickel, "Finite fields: Structure and arithmetics" , Bibliographisches Inst. Mannheim (1993) |
Ultimately periodic sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ultimately_periodic_sequence&oldid=15942