Difference between revisions of "Truncated distribution"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 49043 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Probability distribution|probability distribution]] obtained from a given distribution by transfer of probability mass outside a given interval to within this interval. Let a probability distribution on the line be given by a distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943601.png" />. The truncated distribution corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943602.png" /> is understood to be the distribution function |
| − | t0943601.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943603.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | + | In the particular case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943604.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943605.png" />) the truncated distribution is said to be right truncated (left truncated). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In the particular case | ||
| − | |||
| − | the truncated distribution is said to be right truncated (left truncated). | ||
Together with (1) one considers truncated distribution functions of the form | Together with (1) one considers truncated distribution functions of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943606.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943607.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | In (1) the mass concentrated outside | + | In (1) the mass concentrated outside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943608.png" /> is distributed over the whole of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t0943609.png" />, in (2) it is located at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436010.png" /> (in this case, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436011.png" />, one usually takes for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436012.png" /> the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436013.png" />), and in (3) this mass is located at the extreme points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436015.png" />. |
| − | is distributed over the whole of | ||
| − | in (2) it is located at the point | ||
| − | in this case, when | ||
| − | one usually takes for | ||
| − | the point | ||
| − | and in (3) this mass is located at the extreme points | ||
| − | and | ||
| − | A truncated distribution of the form (1) may be interpreted as follows. Let | + | A truncated distribution of the form (1) may be interpreted as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436016.png" /> be a random variable with distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436017.png" />. Then the truncated distribution coincides with the conditional distribution of the random variable under the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436018.png" />. |
| − | be a random variable with distribution function | ||
| − | Then the truncated distribution coincides with the conditional distribution of the random variable under the condition | ||
| − | The concept of a truncated distribution is closely connected with the concept of a truncated random variable: If | + | The concept of a truncated distribution is closely connected with the concept of a truncated random variable: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436019.png" /> is a random variable, then by a truncated random variable one understands the variable |
| − | is a random variable, then by a truncated random variable one understands the variable | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436020.png" /></td> </tr></table> | |
| − | |||
| − | The distribution of | + | The distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436021.png" /> is a truncated distribution of type (3) (with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436023.png" />) with respect to the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094360/t09436024.png" />. |
| − | is a truncated distribution of type (3) (with | ||
| − | |||
| − | with respect to the distribution of | ||
The truncation operation — passing to the truncated distribution or truncated random variable — is a very widespread technical device. It makes it possible, by a minor change in the initial distribution, to obtain an analytic property — existence of all moments. | The truncation operation — passing to the truncated distribution or truncated random variable — is a very widespread technical device. It makes it possible, by a minor change in the initial distribution, to obtain an analytic property — existence of all moments. | ||
Revision as of 14:53, 7 June 2020
A probability distribution obtained from a given distribution by transfer of probability mass outside a given interval to within this interval. Let a probability distribution on the line be given by a distribution function  . The truncated distribution corresponding to
. The truncated distribution corresponding to 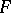 is understood to be the distribution function
is understood to be the distribution function
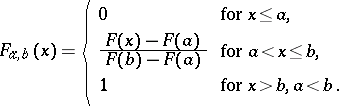 | (1) |
In the particular case  (
( ) the truncated distribution is said to be right truncated (left truncated).
) the truncated distribution is said to be right truncated (left truncated).
Together with (1) one considers truncated distribution functions of the form
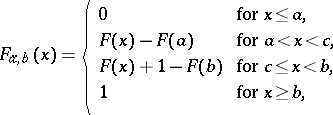 | (2) |
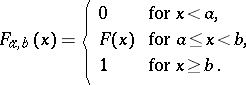 | (3) |
In (1) the mass concentrated outside 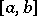 is distributed over the whole of
is distributed over the whole of 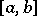 , in (2) it is located at the point
, in (2) it is located at the point  (in this case, when
(in this case, when 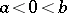 , one usually takes for
, one usually takes for  the point
the point 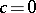 ), and in (3) this mass is located at the extreme points
), and in (3) this mass is located at the extreme points  and
and 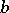 .
.
A truncated distribution of the form (1) may be interpreted as follows. Let 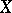 be a random variable with distribution function
be a random variable with distribution function 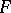 . Then the truncated distribution coincides with the conditional distribution of the random variable under the condition
. Then the truncated distribution coincides with the conditional distribution of the random variable under the condition 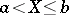 .
.
The concept of a truncated distribution is closely connected with the concept of a truncated random variable: If 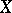 is a random variable, then by a truncated random variable one understands the variable
is a random variable, then by a truncated random variable one understands the variable
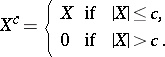 |
The distribution of 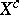 is a truncated distribution of type (3) (with
is a truncated distribution of type (3) (with 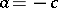 ,
, 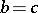 ) with respect to the distribution of
) with respect to the distribution of 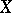 .
.
The truncation operation — passing to the truncated distribution or truncated random variable — is a very widespread technical device. It makes it possible, by a minor change in the initial distribution, to obtain an analytic property — existence of all moments.
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [3] | W. Feller, "An introduction to probability theory and its applications", 1–2 , Wiley (1957–1971) |
| [4] | M. Loève, "Probability theory" , Springer (1977) |
Truncated distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Truncated_distribution&oldid=49484