Trochoid
A plane curve that is the trajectory of a point  inside or outside a circle that rolls upon another circle. A trochoid is called an epitrochoid (Fig.1a, Fig.1b) or a hypotrochoid (Fig.2a, Fig.2b), depending on whether the rolling circle has external or internal contact with the fixed circle.
inside or outside a circle that rolls upon another circle. A trochoid is called an epitrochoid (Fig.1a, Fig.1b) or a hypotrochoid (Fig.2a, Fig.2b), depending on whether the rolling circle has external or internal contact with the fixed circle.

Figure: t094330a

Figure: t094330b

Figure: t094330c

Figure: t094330d
The parametric equations of the epitrochoid are:
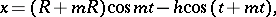 |
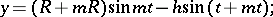 |
and of the hypotrochoid:
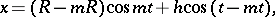 |
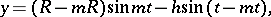 |
where  is the radius of the rolling circle,
is the radius of the rolling circle,  is the radius of the fixed circle,
is the radius of the fixed circle,  is the modulus of the trochoid, and
is the modulus of the trochoid, and  is the distance from the tracing point to the centre of the rolling circle. If
is the distance from the tracing point to the centre of the rolling circle. If  , then the trochoid is called elongated (Fig.1a, Fig.2a), when
, then the trochoid is called elongated (Fig.1a, Fig.2a), when  shortened (Fig.1b, Fig.2b) and when
shortened (Fig.1b, Fig.2b) and when  , an epicycloid or hypocycloid.
, an epicycloid or hypocycloid.
If  , then the trochoid is called a trochoidal rosette; its equation in polar coordinates is
, then the trochoid is called a trochoidal rosette; its equation in polar coordinates is
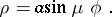 |
For rational values of  the trochoidal rosette is an algebraic curve. If
the trochoidal rosette is an algebraic curve. If  , then the trochoid is called the Pascal limaçon; if
, then the trochoid is called the Pascal limaçon; if  , an ellipse.
, an ellipse.
Trochoids are related to the so-called cycloidal curves (cf. Cycloidal curve). Sometimes the trochoid is called a shortened or elongated cycloid.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
Trochoids play an important role in kinematics. They are used for the construction of gears and engines (see [a2]). Historically, they were a tool for the description of the movement of the planets before N. Copernicus and J. Kepler succeeded to establish the actual view of the dynamics of the solar system.
References
| [a1] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
| [a2] | H.-R. Müller, "Kinematik" , de Gruyter (1963) |
| [a3] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a4] | M. Berger, "Geometry" , 1–2 , Springer (1987) pp. §9.14.34 (Translated from French) |
| [a5] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
Trochoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trochoid&oldid=18583