Triangular matrix

A square matrix for which all entries below (or above) the principal diagonal are zero. In the first case the matrix is called an upper triangular matrix, in the second, a lower triangular matrix. The determinant of a triangular matrix is equal to the product of its diagonal elements.

Comments

A matrix which can be brought to triangular form is called a trigonalizable matrix, cf. Trigonalizable element.

Any -matrix of rank in which the first successive principal minors are different from zero can be written as a product of a lower triangular matrix and an upper triangular matrix , [a1].

Any real matrix can be decomposed in the form , where is orthogonal and is upper triangular, a so-called 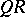-decomposition, or in the form , with orthogonal and lower triangular, a -decomposition or -factorization. Such decompositions play an important role in numerical algorithms, [a2], [a3] (for instance, in computing eigenvalues).

If is non-singular and is required to have its diagonal elements positive, then the -decomposition is unique, [a3], and is given by the Gram–Schmidt orthonormalization procedure, cf. Orthogonalization; Iwasawa decomposition.

References

[a1]	F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1959) pp. 33ff (Translated from Russian)
[a2]	D.M. Young, R.T. Gregory, "A survey of numerical mathematics" , 2 , Addison-Wesley (1973) pp. 921ff
[a3]	W.H. Press, B.P. Flannery, S.A. Teukolsky, W.T. Vetterling, "Numerical recipes" , Cambridge Univ. Press (1986) pp. 357ff