Transfinite induction
A principle enabling one to infer that  holds for every element
holds for every element  of a well-ordered class
of a well-ordered class  if it is established that for each
if it is established that for each  the truth of
the truth of  for all
for all  implies the truth of
implies the truth of  :
:
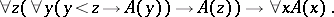 |
When  is the segment of ordinal numbers less than
is the segment of ordinal numbers less than 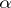 (cf. Ordinal number), the following is an equivalent formulation: If
(cf. Ordinal number), the following is an equivalent formulation: If 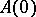 ,
, 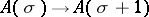 and if
and if  is preserved under limits, i.e.
is preserved under limits, i.e.
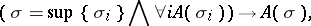 |
then 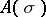 for any
for any 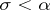 . A special case of transfinite induction is mathematical induction. If the relation
. A special case of transfinite induction is mathematical induction. If the relation  defines on the class
defines on the class  a well-founded tree (i.e. a tree all branches of which terminate), then transfinite induction for such an
a well-founded tree (i.e. a tree all branches of which terminate), then transfinite induction for such an 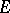 is equivalent to bar induction: If
is equivalent to bar induction: If  is true for all end vertices and is inherited on moving from them towards the root, then
is true for all end vertices and is inherited on moving from them towards the root, then  is true for the root. This form is important in intuitionistic mathematics. The deductive power of a formal system can often be measured in terms of provability of transfinite induction up to various ordinals.
is true for the root. This form is important in intuitionistic mathematics. The deductive power of a formal system can often be measured in terms of provability of transfinite induction up to various ordinals.
Comments
References
| [a1] | S. Feferman, "Theories of finite type related to mathematical practice" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 913–972 |
Transfinite induction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transfinite_induction&oldid=15594