Difference between revisions of "Transfinite diameter"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 49009 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''of a compact set'' | ''of a compact set'' | ||
| − | A characteristic | + | A characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936701.png" /> of a compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936702.png" /> in the complex plane serving as a geometric interpretation of the [[Capacity|capacity]] of this set. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936703.png" /> be a compact infinite set in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936704.png" />-plane. Then the quantity |
| − | of a compact set | ||
| − | in the complex plane serving as a geometric interpretation of the [[Capacity|capacity]] of this set. Let | ||
| − | be a compact infinite set in the | ||
| − | plane. Then the quantity | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936705.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936706.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936707.png" /> is the Euclidean distance between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936708.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t0936709.png" />, is called the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367011.png" />-th diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367012.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367013.png" /> is the Euclidean diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367014.png" />. The points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367015.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367016.png" /> for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367017.png" />. The sequence of quantities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367018.png" /> is non-increasing: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367020.png" /> so that the following limit exists: |
| − | is the Euclidean distance between | ||
| − | and | ||
| − | is called the | ||
| − | th diameter of | ||
| − | In particular, | ||
| − | is the Euclidean diameter of | ||
| − | The points | ||
| − | of | ||
| − | for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for | ||
| − | The sequence of quantities | ||
| − | is non-increasing: | ||
| − | |||
| − | so that the following limit exists: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367021.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | The quantity | + | The quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367022.png" /> is also called the transfinite diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367023.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367024.png" /> is a finite set, then one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367025.png" />. The transfinite diameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367026.png" />, the [[Chebyshev constant|Chebyshev constant]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367027.png" /> and the capacity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367028.png" /> are equal: |
| − | is also called the transfinite diameter of | ||
| − | If | ||
| − | is a finite set, then one has | ||
| − | The transfinite diameter | ||
| − | the [[Chebyshev constant|Chebyshev constant]] | ||
| − | and the capacity | ||
| − | are equal: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367029.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | The transfinite diameter of a set | + | The transfinite diameter of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367030.png" /> has the following properties: 1) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367031.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367032.png" />; 2) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367033.png" /> is a fixed complex number and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367034.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367035.png" />; 3) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367036.png" /> is the set of points at a distance at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367037.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367038.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367039.png" />; 4) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367040.png" /> is the set of roots of the equation |
| − | has the following properties: 1) if | ||
| − | then | ||
| − | 2) if | ||
| − | is a fixed complex number and | ||
| − | then | ||
| − | 3) if | ||
| − | is the set of points at a distance at most | ||
| − | from | ||
| − | then | ||
| − | 4) if | ||
| − | is the set of roots of the equation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367041.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367042.png" /> is a given polynomial and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367043.png" /> runs through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367044.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367045.png" />. The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length. |
| − | is a given polynomial and | ||
| − | runs through | ||
| − | then | ||
| − | The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367046.png" /> be a bounded continuum and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367047.png" /> be the component of the complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367048.png" /> with respect to the extended plane that contains the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367049.png" />. Then the transfinite diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367050.png" /> is equal to the conformal radius of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367051.png" /> (with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367052.png" />; cf. [[Conformal radius of a domain|Conformal radius of a domain]]). |
| − | be a bounded continuum and let | ||
| − | be the component of the complement of | ||
| − | with respect to the extended plane that contains the point | ||
| − | Then the transfinite diameter of | ||
| − | is equal to the conformal radius of | ||
| − | with respect to | ||
| − | cf. [[Conformal radius of a domain|Conformal radius of a domain]]). | ||
| − | The corresponding notions for sets in the hyperbolic and elliptic planes are defined as follows. Consider as a model of the hyperbolic plane the disc | + | The corresponding notions for sets in the hyperbolic and elliptic planes are defined as follows. Consider as a model of the hyperbolic plane the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367053.png" /> with metric defined by the line element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367054.png" /> and suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367055.png" /> is a closed infinite set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367056.png" />. Then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367058.png" />-th hyperbolic diameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367059.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367060.png" /> is defined by (1) in which |
| − | with metric defined by the line element | ||
| − | and suppose that | ||
| − | is a closed infinite set in | ||
| − | Then the | ||
| − | th hyperbolic diameter | ||
| − | of | ||
| − | is defined by (1) in which | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367061.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | + | is the hyperbolic pseudo-distance between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367062.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367063.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367064.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367065.png" /> is the hyperbolic distance between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367066.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367067.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367068.png" /> (see [[Hyperbolic metric|Hyperbolic metric]]). As in the Euclidean case, the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367069.png" /> is non-increasing and the following limit exists: | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367070.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | It is called the hyperbolic transfinite diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367071.png" />. Define the hyperbolic Chebyshev constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367072.png" /> and the hyperbolic capacity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367073.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367074.png" /> via the hyperbolic pseudo-distance (2) between the points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367075.png" /> by analogy with the Chebyshev constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367076.png" /> and capacity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367077.png" /> defined via the Euclidean distance between points of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367078.png" />-plane. Then one obtains | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367079.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The hyperbolic transfinite diameter is invariant under the full group of hyperbolic isometries. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367080.png" /> is a continuum, then there is a simple relationship between the hyperbolic transfinite diameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367081.png" /> and conformal mapping. Namely, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367082.png" /> be a continuum in the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367083.png" /> such that the complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367084.png" /> with respect to this disc is conformally equivalent to the annulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367085.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367086.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367087.png" />. | |
| − | |||
| − | |||
| − | + | Consider as a model of the elliptic plane the extended complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367088.png" />-plane with the metric of its Riemann sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367089.png" /> of diameter 1, tangent to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367090.png" />-plane at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367091.png" />, that is, the metric defined by the line element | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367092.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | furthermore, let the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367093.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367094.png" /> be identified; these correspond to diametrically-opposite points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367095.png" /> under stereographic projection of the extended <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367096.png" />-plane onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367097.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367098.png" /> be a closed infinite set in the extended <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t09367099.png" />-plane, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670100.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670101.png" />. Then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670103.png" />-th elliptic diameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670104.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670105.png" /> is defined by (1), in which | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670106.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | + | is the elliptic pseudo-distance between points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670108.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670109.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670110.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670111.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670112.png" />) is the elliptic distance between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670113.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670114.png" />. As in the previous cases, the sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670115.png" /> is non-increasing and the following limit, called the elliptic transfinite diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670116.png" />, exists: | |
| − | and | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | where | ||
| − | |||
| − | |||
| − | of | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670117.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | Define the elliptic Chebyshev constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670118.png" /> and the elliptic capacity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670119.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670120.png" /> via the elliptic pseudo-distance (3). Then one obtains: | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670121.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The elliptic transfinite diameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670122.png" /> is invariant under the group of fractional-linear transformations | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670123.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | of the extended <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670124.png" />-plane onto itself, supplemented by the group of reflections in the elliptic lines. The first of these groups is isomorphic to the group of reflections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670125.png" /> about planes passing through its centre. With this definition the elliptic transfinite diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670126.png" /> is related to conformal mapping in the following way. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670127.png" /> is a continuum in the extended <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670128.png" />-plane, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670129.png" />, and the complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670130.png" /> with respect to the extended plane is conformally equivalent to the annulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670132.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670133.png" />. | |
| − | |||
| − | |||
| − | The | + | The notion of the transfinite diameter can be generalized to compacta <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670134.png" /> in a multi-dimensional Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670135.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670136.png" />, and is connected with [[Potential theory|potential theory]]. Let, for points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670137.png" />, |
| − | is | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670138.png" /></td> </tr></table> | |
| − | |||
| − | + | be a fundamental solution of the [[Laplace equation|Laplace equation]], and for the set of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670139.png" />, let | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670140.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Then for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670141.png" /> one has | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670142.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | while for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670143.png" /> it is expedient (see [[#References|[4]]]) to take | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670144.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | . | ||
| − | |||
| − | + | ====References==== | |
| − | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Fekete, "Ueber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten" ''Math. Z.'' , '''17''' (1923) pp. 228–249</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Pólya, G. Szegö, "Ueber den transfiniten Durchmesser (Kapazitätskonstante) von ebenen und räumlichen Punktmengen" ''J. Reine Angew. Math.'' , '''165''' (1931) pp. 4–49</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1959)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Kühnau, "Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene" , Deutsch. Verlag Wissenschaft. (1974)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Outer radius is another term for transfinite diameter. See [[#References|[a1]]] for a survey on connections between transfinite diameter, [[Robin constant|Robin constant]] and [[Capacity|capacity]] in | + | Outer radius is another term for transfinite diameter. See [[#References|[a1]]] for a survey on connections between transfinite diameter, [[Robin constant|Robin constant]] and [[Capacity|capacity]] in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670145.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670146.png" />. |
| − | or | ||
| − | The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with | + | The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670147.png" /> is a root of a Vandermondian determinant: |
| − | is a root of a Vandermondian determinant: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670148.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670149.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In | + | In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670150.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670151.png" /> be an ordered system of monomials of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670152.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670153.png" /> be a point in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670154.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670155.png" /> is defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670156.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670157.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670158.png" />. The related capacity is the one associated to the complex Monge–Ampère operator. |
| − | let | ||
| − | be an ordered system of monomials of degree | ||
| − | and let | ||
| − | be a point in | ||
| − | Then | ||
| − | is defined as | ||
| − | |||
| − | and | ||
| − | The related capacity is the one associated to the complex Monge–Ampère operator. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , ''Potential theory. Survey and problems (Prague, 1987)'' , ''Lect. notes in math.'' , '''1344''' , Plenum (1988) pp. 103–120</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Siciak, "Extremal plurisubharmonic functions and capacities in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670159.png" />" , ''Sophia Kokyuroku in Math.'' , '''14''' , Dept. Math. Sophia Univ. Tokyo (1982)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , ''Potential theory. Survey and problems (Prague, 1987)'' , ''Lect. notes in math.'' , '''1344''' , Plenum (1988) pp. 103–120</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Siciak, "Extremal plurisubharmonic functions and capacities in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670159.png" />" , ''Sophia Kokyuroku in Math.'' , '''14''' , Dept. Math. Sophia Univ. Tokyo (1982)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
of a compact set
A characteristic 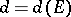 of a compact set
of a compact set 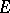 in the complex plane serving as a geometric interpretation of the capacity of this set. Let
in the complex plane serving as a geometric interpretation of the capacity of this set. Let 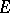 be a compact infinite set in the
be a compact infinite set in the  -plane. Then the quantity
-plane. Then the quantity
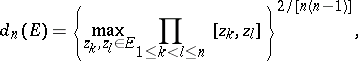 | (1) |
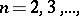 |
where  is the Euclidean distance between
is the Euclidean distance between  and
and 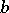 , is called the
, is called the  -th diameter of
-th diameter of 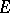 . In particular,
. In particular, 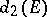 is the Euclidean diameter of
is the Euclidean diameter of 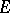 . The points
. The points 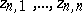 of
of 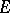 for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for
for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for 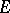 . The sequence of quantities
. The sequence of quantities 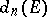 is non-increasing:
is non-increasing: 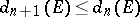 ,
, 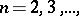 so that the following limit exists:
so that the following limit exists:
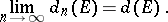 |
The quantity 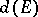 is also called the transfinite diameter of
is also called the transfinite diameter of 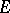 . If
. If 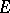 is a finite set, then one has
is a finite set, then one has 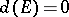 . The transfinite diameter
. The transfinite diameter 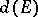 , the Chebyshev constant
, the Chebyshev constant 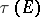 and the capacity
and the capacity 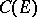 are equal:
are equal:
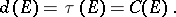 |
The transfinite diameter of a set 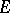 has the following properties: 1) if
has the following properties: 1) if 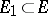 , then
, then 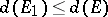 ; 2) if
; 2) if  is a fixed complex number and
is a fixed complex number and 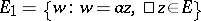 , then
, then 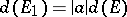 ; 3) if
; 3) if 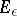 is the set of points at a distance at most
is the set of points at a distance at most  from
from 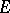 , then
, then 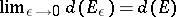 ; 4) if
; 4) if 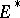 is the set of roots of the equation
is the set of roots of the equation
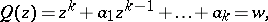 |
where 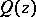 is a given polynomial and
is a given polynomial and 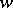 runs through
runs through 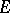 , then
, then 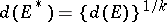 . The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length.
. The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length.
Let 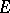 be a bounded continuum and let
be a bounded continuum and let 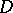 be the component of the complement of
be the component of the complement of 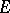 with respect to the extended plane that contains the point
with respect to the extended plane that contains the point 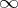 . Then the transfinite diameter of
. Then the transfinite diameter of 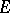 is equal to the conformal radius of
is equal to the conformal radius of 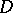 (with respect to
(with respect to 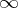 ; cf. Conformal radius of a domain).
; cf. Conformal radius of a domain).
The corresponding notions for sets in the hyperbolic and elliptic planes are defined as follows. Consider as a model of the hyperbolic plane the disc 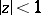 with metric defined by the line element
with metric defined by the line element 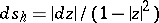 and suppose that
and suppose that 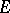 is a closed infinite set in
is a closed infinite set in 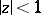 . Then the
. Then the  -th hyperbolic diameter
-th hyperbolic diameter 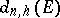 of
of 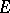 is defined by (1) in which
is defined by (1) in which
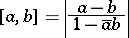 | (2) |
is the hyperbolic pseudo-distance between  and
and 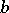 , that is,
, that is, 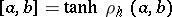 , where
, where 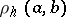 is the hyperbolic distance between
is the hyperbolic distance between  and
and 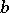 in
in 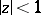 (see Hyperbolic metric). As in the Euclidean case, the sequence
(see Hyperbolic metric). As in the Euclidean case, the sequence 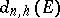 is non-increasing and the following limit exists:
is non-increasing and the following limit exists:
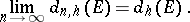 |
It is called the hyperbolic transfinite diameter of 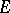 . Define the hyperbolic Chebyshev constant
. Define the hyperbolic Chebyshev constant 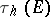 and the hyperbolic capacity
and the hyperbolic capacity 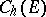 of
of 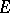 via the hyperbolic pseudo-distance (2) between the points of
via the hyperbolic pseudo-distance (2) between the points of 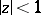 by analogy with the Chebyshev constant
by analogy with the Chebyshev constant 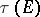 and capacity
and capacity 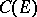 defined via the Euclidean distance between points of the
defined via the Euclidean distance between points of the  -plane. Then one obtains
-plane. Then one obtains
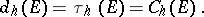 |
The hyperbolic transfinite diameter is invariant under the full group of hyperbolic isometries. If 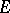 is a continuum, then there is a simple relationship between the hyperbolic transfinite diameter
is a continuum, then there is a simple relationship between the hyperbolic transfinite diameter 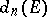 and conformal mapping. Namely, let
and conformal mapping. Namely, let 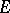 be a continuum in the disc
be a continuum in the disc 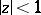 such that the complement of
such that the complement of 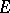 with respect to this disc is conformally equivalent to the annulus
with respect to this disc is conformally equivalent to the annulus 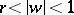 ,
, 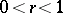 . Then
. Then 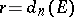 .
.
Consider as a model of the elliptic plane the extended complex  -plane with the metric of its Riemann sphere
-plane with the metric of its Riemann sphere 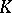 of diameter 1, tangent to the
of diameter 1, tangent to the  -plane at the point
-plane at the point 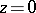 , that is, the metric defined by the line element
, that is, the metric defined by the line element
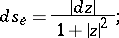 |
furthermore, let the points  and
and 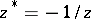 be identified; these correspond to diametrically-opposite points of
be identified; these correspond to diametrically-opposite points of 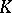 under stereographic projection of the extended
under stereographic projection of the extended  -plane onto
-plane onto 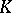 . Let
. Let 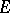 be a closed infinite set in the extended
be a closed infinite set in the extended  -plane,
-plane, 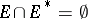 , where
, where 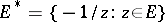 . Then the
. Then the  -th elliptic diameter
-th elliptic diameter 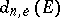 of
of 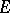 is defined by (1), in which
is defined by (1), in which
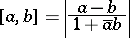 | (3) |
is the elliptic pseudo-distance between points  and
and 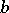 of
of 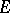 , that is,
, that is, 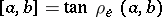 , where
, where 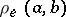 (
(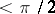 ) is the elliptic distance between
) is the elliptic distance between  and
and 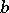 . As in the previous cases, the sequence
. As in the previous cases, the sequence 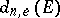 is non-increasing and the following limit, called the elliptic transfinite diameter of
is non-increasing and the following limit, called the elliptic transfinite diameter of 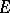 , exists:
, exists:
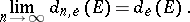 |
Define the elliptic Chebyshev constant 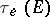 and the elliptic capacity
and the elliptic capacity 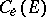 of
of 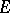 via the elliptic pseudo-distance (3). Then one obtains:
via the elliptic pseudo-distance (3). Then one obtains:
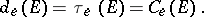 |
The elliptic transfinite diameter 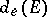 is invariant under the group of fractional-linear transformations
is invariant under the group of fractional-linear transformations
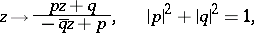 |
of the extended  -plane onto itself, supplemented by the group of reflections in the elliptic lines. The first of these groups is isomorphic to the group of reflections of
-plane onto itself, supplemented by the group of reflections in the elliptic lines. The first of these groups is isomorphic to the group of reflections of 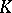 about planes passing through its centre. With this definition the elliptic transfinite diameter of
about planes passing through its centre. With this definition the elliptic transfinite diameter of 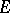 is related to conformal mapping in the following way. If
is related to conformal mapping in the following way. If 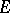 is a continuum in the extended
is a continuum in the extended  -plane,
-plane, 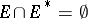 , and the complement of
, and the complement of 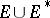 with respect to the extended plane is conformally equivalent to the annulus
with respect to the extended plane is conformally equivalent to the annulus 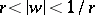 ,
, 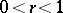 , then
, then 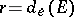 .
.
The notion of the transfinite diameter can be generalized to compacta 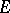 in a multi-dimensional Euclidean space
in a multi-dimensional Euclidean space 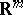 ,
, 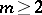 , and is connected with potential theory. Let, for points
, and is connected with potential theory. Let, for points 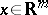 ,
,
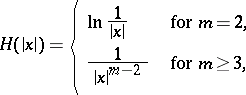 |
be a fundamental solution of the Laplace equation, and for the set of points 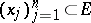 , let
, let
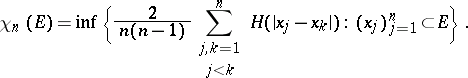 |
Then for 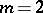 one has
one has
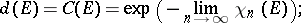 |
while for 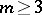 it is expedient (see [4]) to take
it is expedient (see [4]) to take
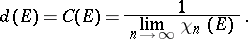 |
References
| [1] | M. Fekete, "Ueber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten" Math. Z. , 17 (1923) pp. 228–249 |
| [2] | G. Pólya, G. Szegö, "Ueber den transfiniten Durchmesser (Kapazitätskonstante) von ebenen und räumlichen Punktmengen" J. Reine Angew. Math. , 165 (1931) pp. 4–49 |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [4] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) |
| [5] | V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian) |
| [6] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1959) |
| [7] | R. Kühnau, "Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene" , Deutsch. Verlag Wissenschaft. (1974) |
Comments
Outer radius is another term for transfinite diameter. See [a1] for a survey on connections between transfinite diameter, Robin constant and capacity in 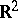 or
or 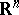 .
.
The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with  is a root of a Vandermondian determinant:
is a root of a Vandermondian determinant:
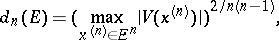 |
where
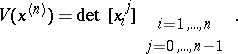 |
In 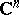 , let
, let 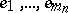 be an ordered system of monomials of degree
be an ordered system of monomials of degree 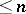 and let
and let 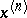 be a point in
be a point in 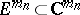 . Then
. Then 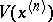 is defined as
is defined as 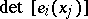 ,
, 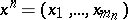 , and
, and 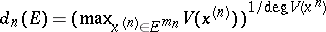 . The related capacity is the one associated to the complex Monge–Ampère operator.
. The related capacity is the one associated to the complex Monge–Ampère operator.
References
| [a1] | R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , Potential theory. Survey and problems (Prague, 1987) , Lect. notes in math. , 1344 , Plenum (1988) pp. 103–120 |
| [a2] | M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991) |
| [a3] | J. Siciak, "Extremal plurisubharmonic functions and capacities in 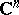 " , Sophia Kokyuroku in Math. , 14 , Dept. Math. Sophia Univ. Tokyo (1982) " , Sophia Kokyuroku in Math. , 14 , Dept. Math. Sophia Univ. Tokyo (1982) |
Transfinite diameter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transfinite_diameter&oldid=49476