Trace of a square matrix
From Encyclopedia of Mathematics
The sum of the entries on the main diagonal of this matrix. The trace of a matrix  is denoted by
is denoted by  ,
,  or
or  :
:
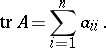 |
Let  be a square matrix of order
be a square matrix of order  over a field
over a field  . The trace of
. The trace of  coincides with the sum of the roots of the characteristic polynomial of
coincides with the sum of the roots of the characteristic polynomial of  . If
. If  is a field of characteristic 0, then the
is a field of characteristic 0, then the  traces
traces 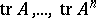 uniquely determine the characteristic polynomial of
uniquely determine the characteristic polynomial of  . In particular,
. In particular,  is nilpotent if and only if
is nilpotent if and only if 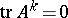 for all
for all  .
.
If 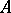 and
and  are square matrices of the same order over
are square matrices of the same order over 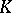 , and
, and 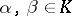 , then
, then
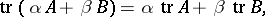 |
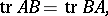 |
while if 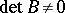 ,
,
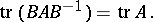 |
The trace of the tensor (Kronecker) product of square matrices over a field is equal to the product of the traces of the factors.
Comments
References
| [a1] | P.M. Cohn, "Algebra" , 1 , Wiley (1982) pp. 336 |
| [a2] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1959) (Translated from Russian) |
How to Cite This Entry:
Trace of a square matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace_of_a_square_matrix&oldid=16032
Trace of a square matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace_of_a_square_matrix&oldid=16032
This article was adapted from an original article by D.A. Suprunenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article