Topological ring
A ring 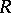 that is a topological space, such that the mappings
that is a topological space, such that the mappings
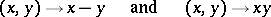 |
are continuous. A topological ring 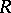 is called separated if it is separated as a topological space (cf. Separation axiom). In this case
is called separated if it is separated as a topological space (cf. Separation axiom). In this case 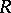 is a Hausdorff space. Any subring
is a Hausdorff space. Any subring 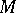 of a topological ring
of a topological ring 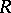 , and also the quotient ring
, and also the quotient ring 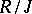 by an ideal
by an ideal 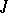 , is a topological ring. If
, is a topological ring. If 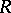 is separated and the ideal
is separated and the ideal 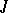 is closed, then
is closed, then 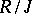 is a separated topological ring. The closure
is a separated topological ring. The closure 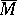 of a subring
of a subring 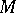 in
in 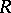 is also a topological ring. A direct product of topological rings is a topological ring in a natural way.
is also a topological ring. A direct product of topological rings is a topological ring in a natural way.
A homomorphism of topological rings is a ring homomorphism which is also a continuous mapping. If 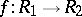 is such a homomorphism, where
is such a homomorphism, where 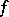 is moreover an epimorphism and an open mapping, then
is moreover an epimorphism and an open mapping, then 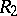 is isomorphic as a topological ring to
is isomorphic as a topological ring to 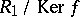 . Banach algebras are an example of topological rings. An important type of topological ring is defined by the property that it has a fundamental system of neighbourhoods of zero consisting of some set of ideals. For example, to any ideal
. Banach algebras are an example of topological rings. An important type of topological ring is defined by the property that it has a fundamental system of neighbourhoods of zero consisting of some set of ideals. For example, to any ideal 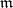 in a commutative ring
in a commutative ring 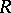 one can associate the
one can associate the 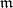 -adic topology, in which the sets
-adic topology, in which the sets 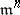 for all natural numbers
for all natural numbers  form a fundamental system of neighbourhoods of zero. This topology is separated if the condition
form a fundamental system of neighbourhoods of zero. This topology is separated if the condition
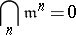 |
is satisfied.
For a topological ring 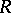 one can define its completion
one can define its completion  , which is a complete topological ring, and a separated topological ring
, which is a complete topological ring, and a separated topological ring 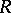 can be imbedded as an everywhere-dense subset in
can be imbedded as an everywhere-dense subset in 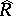 , which is also separated in this case. The additive group of the ring
, which is also separated in this case. The additive group of the ring 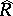 coincides with the completion of the additive group of
coincides with the completion of the additive group of 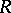 , as an Abelian topological group.
, as an Abelian topological group.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [3] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [4] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
Topological ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topological_ring&oldid=17173