Difference between revisions of "Thom spectrum"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | t0926901.png | ||
| + | $#A+1 = 34 n = 2 | ||
| + | $#C+1 = 34 : ~/encyclopedia/old_files/data/T092/T.0902690 Thom spectrum | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | Let | + | A [[Spectrum of spaces|spectrum of spaces]], equivalent to the spectrum associated to a certain structure series (cf. [[B-Phi-structure| $ ( B, \phi ) $- |
| + | structure]]). | ||
| + | |||
| + | Let $ ( B _ {n} , \phi _ {n} , g _ {n} ) $ | ||
| + | be a structure series, and let $ \xi _ {n} $ | ||
| + | be the bundle over $ B _ {n} $ | ||
| + | induced by the mapping $ \phi _ {n} : B _ {n} \rightarrow \mathop{\rm BO} _ {n} $. | ||
| + | Let $ T _ {n} $ | ||
| + | be the [[Thom space|Thom space]] of $ \xi _ {n} $. | ||
| + | The mapping $ g _ {n} $ | ||
| + | induces a mapping $ S _ {n} : ST _ {n} \rightarrow T _ {n + 1 } $, | ||
| + | where $ S $ | ||
| + | is [[Suspension|suspension]] and $ ST \xi _ {n} = T( \xi _ {n} \oplus \theta ) $( | ||
| + | $ \theta $ | ||
| + | is the one-dimensional trivial bundle). One obtains a spectrum of spaces $ \{ T \xi _ {n} \} = T ( B, \phi , g) $, | ||
| + | associated with the structure series $ ( B _ {n} , \phi _ {n} , g _ {n} ) $, | ||
| + | and a Thom spectrum is any spectrum that is (homotopy) equivalent to a spectrum of the form $ T ( B, \phi , g) $. | ||
| + | It represents $ ( B, \phi ) $- | ||
| + | cobordism theory. Thus, the series of classical Lie groups $ O _ {k} $, | ||
| + | $ \mathop{\rm SO} _ {k} $, | ||
| + | $ U _ {k} $, | ||
| + | and $ \mathop{\rm Sp} _ {k} $ | ||
| + | lead to the Thom spectra $ \mathop{\rm TBO} $, | ||
| + | $ \mathop{\rm TBSO} $, | ||
| + | $ \mathop{\rm TBU} $, | ||
| + | and $ \mathop{\rm TBSp} $. | ||
| + | |||
| + | Let $ \beta _ {n} $ | ||
| + | be Artin's braid group on $ n $ | ||
| + | strings (cf. [[Braid theory|Braid theory]]). The homomorphism $ \beta _ {n} \rightarrow S _ {n} \subset O _ {n} $, | ||
| + | where $ S _ {n} $ | ||
| + | is the symmetric group, yields a mapping $ B \beta _ {n} \rightarrow \mathop{\rm BO} _ {n} $ | ||
| + | such that a structure series arises ( $ \beta _ {n} $ | ||
| + | is canonically imbedded in $ \beta _ {n + 1 } $). | ||
| + | The corresponding Thom spectrum is equivalent to the Eilenberg–MacLane spectrum $ K ( \mathbf Z /2) = \{ K ( \mathbf Z /2, n) \} $, | ||
| + | so that $ K ( \mathbf Z /2) $ | ||
| + | is a Thom spectrum (cf. [[#References|[1]]], [[#References|[2]]]). Analogously, $ K ( \mathbf Z ) $ | ||
| + | is a Thom spectrum, but using sphere bundles, [[#References|[3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Mahowold, "A new infinite family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092690/t09269035.png" />" ''Topology'' , '''16''' (1977) pp. 249–256</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Priddy, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092690/t09269036.png" /> as a Thom spectrum" ''Proc. Amer. Math. Soc.'' , '''70''' : 2 (1978) pp. 207–208</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Mahowold, "Ring spectra which are Thom complexes" ''Duke Math. J.'' , '''46''' : 3 (1979) pp. 549–559</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Mahowold, "A new infinite family in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092690/t09269035.png" />" ''Topology'' , '''16''' (1977) pp. 249–256</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Priddy, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092690/t09269036.png" /> as a Thom spectrum" ''Proc. Amer. Math. Soc.'' , '''70''' : 2 (1978) pp. 207–208</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Mahowold, "Ring spectra which are Thom complexes" ''Duke Math. J.'' , '''46''' : 3 (1979) pp. 549–559</TD></TR></table> | ||
Latest revision as of 08:25, 6 June 2020
A spectrum of spaces, equivalent to the spectrum associated to a certain structure series (cf. $ ( B, \phi ) $-
structure).
Let $ ( B _ {n} , \phi _ {n} , g _ {n} ) $ be a structure series, and let $ \xi _ {n} $ be the bundle over $ B _ {n} $ induced by the mapping $ \phi _ {n} : B _ {n} \rightarrow \mathop{\rm BO} _ {n} $. Let $ T _ {n} $ be the Thom space of $ \xi _ {n} $. The mapping $ g _ {n} $ induces a mapping $ S _ {n} : ST _ {n} \rightarrow T _ {n + 1 } $, where $ S $ is suspension and $ ST \xi _ {n} = T( \xi _ {n} \oplus \theta ) $( $ \theta $ is the one-dimensional trivial bundle). One obtains a spectrum of spaces $ \{ T \xi _ {n} \} = T ( B, \phi , g) $, associated with the structure series $ ( B _ {n} , \phi _ {n} , g _ {n} ) $, and a Thom spectrum is any spectrum that is (homotopy) equivalent to a spectrum of the form $ T ( B, \phi , g) $. It represents $ ( B, \phi ) $- cobordism theory. Thus, the series of classical Lie groups $ O _ {k} $, $ \mathop{\rm SO} _ {k} $, $ U _ {k} $, and $ \mathop{\rm Sp} _ {k} $ lead to the Thom spectra $ \mathop{\rm TBO} $, $ \mathop{\rm TBSO} $, $ \mathop{\rm TBU} $, and $ \mathop{\rm TBSp} $.
Let $ \beta _ {n} $ be Artin's braid group on $ n $ strings (cf. Braid theory). The homomorphism $ \beta _ {n} \rightarrow S _ {n} \subset O _ {n} $, where $ S _ {n} $ is the symmetric group, yields a mapping $ B \beta _ {n} \rightarrow \mathop{\rm BO} _ {n} $ such that a structure series arises ( $ \beta _ {n} $ is canonically imbedded in $ \beta _ {n + 1 } $). The corresponding Thom spectrum is equivalent to the Eilenberg–MacLane spectrum $ K ( \mathbf Z /2) = \{ K ( \mathbf Z /2, n) \} $, so that $ K ( \mathbf Z /2) $ is a Thom spectrum (cf. [1], [2]). Analogously, $ K ( \mathbf Z ) $ is a Thom spectrum, but using sphere bundles, [3].
References
| [1] | M. Mahowold, "A new infinite family in 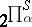 " Topology , 16 (1977) pp. 249–256 " Topology , 16 (1977) pp. 249–256 |
| [2] | S. Priddy, " as a Thom spectrum" Proc. Amer. Math. Soc. , 70 : 2 (1978) pp. 207–208 as a Thom spectrum" Proc. Amer. Math. Soc. , 70 : 2 (1978) pp. 207–208 |
| [3] | M. Mahowold, "Ring spectra which are Thom complexes" Duke Math. J. , 46 : 3 (1979) pp. 549–559 |
Thom spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom_spectrum&oldid=18456