Theta-series
 -series
-series
A series of functions used in the representation of automorphic forms and functions (cf. Automorphic form; Automorphic function).
Let  be a domain in the complex space
be a domain in the complex space  ,
,  , and let
, and let  be the discrete group of automorphisms of
be the discrete group of automorphisms of  . If
. If 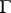 is finite, then any function
is finite, then any function  ,
,  , meromorphic on
, meromorphic on  gives rise to an automorphic function
gives rise to an automorphic function
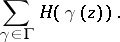 |
For infinite groups one needs convergence multipliers to obtain a theta-series. A Poincaré series, associated to a group  , is a series of the form
, is a series of the form
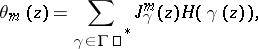 | (1) |
where  is the Jacobian of the function
is the Jacobian of the function  and
and 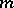 is an integer called the weight or the order. The asterisk means that summation is over those
is an integer called the weight or the order. The asterisk means that summation is over those  which yield distinct terms in the series. Under a mapping
which yield distinct terms in the series. Under a mapping 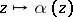 ,
, 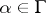 , the function
, the function  is transformed according to the law
is transformed according to the law  , and hence is an automorphic function of weight
, and hence is an automorphic function of weight  , associated to
, associated to 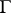 . The quotient of two theta-series of the same weight gives an automorphic function.
. The quotient of two theta-series of the same weight gives an automorphic function.
The theta-series
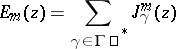 |
is called an Eisenstein theta-series, or simply an Eisenstein series, associated with 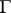 .
.
H. Poincaré, in a series of articles in the 1880's, developed the theory of theta-series in connection with the study of automorphic functions of one complex variable. Let  be a discrete Fuchsian group of fractional-linear transformations
be a discrete Fuchsian group of fractional-linear transformations
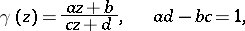 |
mapping the unit disc 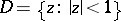 onto itself. For this case the Poincaré series has the form
onto itself. For this case the Poincaré series has the form
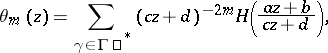 | (2) |
where  , for example, is a bounded holomorphic function on
, for example, is a bounded holomorphic function on  . Under the hypothesis that
. Under the hypothesis that 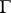 acts freely on
acts freely on  and that the quotient space
and that the quotient space  is compact, it has been shown that the series (2) converges absolutely and uniformly on
is compact, it has been shown that the series (2) converges absolutely and uniformly on  for
for  . With the stated conditions on
. With the stated conditions on 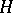 and
and  , this assertion holds also for the series (1) in the case where
, this assertion holds also for the series (1) in the case where  is a bounded domain in
is a bounded domain in 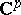 . For certain Fuchsian groups the series (2) converges also for
. For certain Fuchsian groups the series (2) converges also for 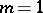 .
.
The term "theta-series" is also applied to series expansions of theta-functions, which are used in the representation of elliptic functions (cf. Jacobi elliptic functions) and Abelian functions (cf. Theta-function; Abelian function).
References
| [1] | L.R. Ford, "Automorphic functions" , Chelsea, reprint (1951) |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [3] | R. Fricke, F. Klein, "Vorlesungen über die Theorie der automorphen Funktionen" , 1–2 , Teubner (1926) |
Comments
Let  be a lattice. The theta-series of the lattice
be a lattice. The theta-series of the lattice  is defined by
is defined by
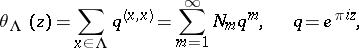 |
where  is the number of points in
is the number of points in  of squared length
of squared length  . For instance, if
. For instance, if  is the lattice
is the lattice  , then
, then  is the number of ways of representing
is the number of ways of representing 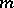 as a sum of four integral squares.
as a sum of four integral squares.
For the lattice  the theta-series is
the theta-series is
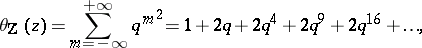 |
which is the Jacobi theta-function 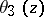 .
.
For more details on theta-series of lattices, including formulas and tables for many (series of) important lattices such as root lattices and the Leech lattice, and applications, cf. [a2].
References
| [a1] | A. Weil, "Elliptic functions according to Eisenstein and Kronecker" , Springer (1976) |
| [a2] | J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988) |
Theta-series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Theta-series&oldid=23995