Tamagawa number
The volume of a homogeneous space 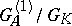 associated with the group of adèles (cf. Adèle) of a connected linear algebraic group
associated with the group of adèles (cf. Adèle) of a connected linear algebraic group  defined over a global field
defined over a global field 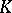 with respect to the Tamagawa measure. Here
with respect to the Tamagawa measure. Here 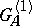 is the subgroup of
is the subgroup of 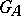 consisting of those adèles
consisting of those adèles 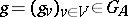 for which
for which
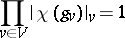 |
for any character 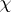 of
of 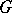 which is defined over
which is defined over 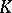 (the product is taken with respect to all valuations
(the product is taken with respect to all valuations  in the set
in the set 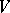 of normalized valuations of
of normalized valuations of  ). The finiteness of the Tamagawa number follows from reduction theory (see [5]).
). The finiteness of the Tamagawa number follows from reduction theory (see [5]).
When describing the values of 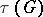 it is convenient to distinguish the cases of unipotent groups, algebraic tori and semi-simple groups. For unipotent groups the Tamagawa number is always equal to 1. If
it is convenient to distinguish the cases of unipotent groups, algebraic tori and semi-simple groups. For unipotent groups the Tamagawa number is always equal to 1. If 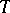 is an algebraic
is an algebraic 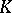 -torus, then
-torus, then
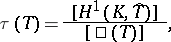 |
where 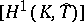 and
and 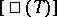 are the order of the one-dimensional Galois cohomology group of the module of rational characters
are the order of the one-dimensional Galois cohomology group of the module of rational characters 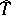 of the torus
of the torus 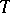 and the order of its Shafarevich–Tate group, respectively. On the basis of this formula an example was constructed of a torus for which
and the order of its Shafarevich–Tate group, respectively. On the basis of this formula an example was constructed of a torus for which 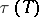 is not an integer [8]. The determination of the Tamagawa number of a semi-simple group over a number field can be reduced to the case of a simply-connected group [9]: Let
is not an integer [8]. The determination of the Tamagawa number of a semi-simple group over a number field can be reduced to the case of a simply-connected group [9]: Let 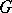 be a semi-simple
be a semi-simple 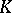 -group, let
-group, let 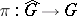 be the universal covering which is defined over
be the universal covering which is defined over 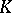 , let
, let 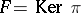 be the fundamental group of
be the fundamental group of 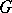 , and let
, and let 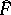 be its character group; then
be its character group; then
 |
where 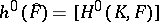 , and
, and 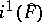 is the order of the kernel of the canonical mapping
is the order of the kernel of the canonical mapping
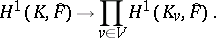 |
It is the conjectured that for all simply-connected groups the Tamagawa number is equal to 1 (the Weil conjecture). This was proved for most types of simple groups over number fields ([3], [4], [7]), and also for Chevalley groups over number fields (see [2]) and over global function fields [6].
References
| [1] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [2] | , Arithmetic groups and automorphic functions , Moscow (1969) (In Russian; translated from English and French) |
| [3] | A. Weil, "Sur certaines groupes d'opérateurs unitaires" Acta Math. , 111 (1964) pp. 143–211 |
| [4] | A. Weil, "Sur la formule de Siegel dans la théorie des groupes classiques" Acta Math. , 113 (1965) pp. 1–87 |
| [5] | V.P. Platonov, "The arithmetic theory of algebraic groups" Russian Math. Surveys , 37 : 3 (1982) pp. 1–62 Uspekhi Mat. Nauk , 37 : 3 (1982) pp. 3–54 |
| [6] | G. Harder, "Chevalley groups over function fields and automorphic forms" Ann. of Math. , 100 (1974) pp. 249–306 |
| [7] | J.G.M. Mars, "The Tamagawa number of 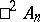 " Ann. of Math. , 89 (1969) pp. 557–574 " Ann. of Math. , 89 (1969) pp. 557–574 |
| [8] | T. Ono, "On the Tamagawa number of algebraic tori" Ann. of Math. , 78 (1963) pp. 47–73 |
| [9] | T. Ono, "On the relative theory of Tamagawa numbers" Ann. of Math. , 82 (1965) pp. 88–111 |
Comments
The Shafarevich–Tate group is also called Tate–Shafarevich group; cf. Galois cohomology for its definition.
For the relation between 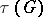 and
and 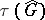 see [a1].
see [a1].
Weil's conjecture has been proved by R. Kottwitz [a2] for number fields, modulo the validity of the Hasse principle. (The latter has also been established.)
References
| [a1] | R.E. Kottwitz, "Stable trace formula: cuspidal tempered terms" Duke Math. J. , 51 (1984) pp. 611–650 |
| [a2] | R.E. Kottwitz, "Tamagawa numbers" Ann. of Math. , 127 (1988) pp. 629–646 |
Tamagawa number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tamagawa_number&oldid=13490