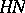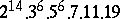Talk:Sporadic simple group
From Encyclopedia of Mathematics
A simple finite group that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table.'
<tbody> </tbody>
|
References
| [1] | S.A. Syskin, "Abstract properties of the simple sporadic groups" Russian Math. Surveys , 35 : 5 (1980) pp. 209–246 Uspekhi Mat. Nauk , 35 : 5 (1980) pp. 181–212 |
| [2] | M. Aschbacher, "The finite simple groups and their classification" , Yale Univ. Press (1980) |
Comments
The recent classification of the finite simple groups (1981) has led to the conclusion that — up to a uniqueness proof for the Monster as the only simple group of its order with certain additional properties — every non-Abelian finite simple group is isomorphic to: an alternating group on at least  letters, a group of (twisted or untwisted) Lie type, or one of the above
letters, a group of (twisted or untwisted) Lie type, or one of the above 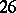 sporadic groups. See [a2] for a discussion of the proof.
sporadic groups. See [a2] for a discussion of the proof.
References
| [a1] | J.H. Conway, R.T. Curtis, S.P. Norton, R.A. Parker, R.A. Wilson, "Atlas of finite groups" , Clarendon Press (1985) |
| [a2] | D. Gorenstein, "Finite simple groups. An introduction to their classification" , Plenum (1982) |
How to Cite This Entry:
Sporadic simple group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sporadic_simple_group&oldid=25775
Sporadic simple group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sporadic_simple_group&oldid=25775
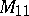

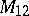
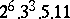

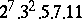
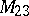


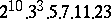
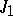
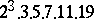
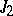 ,
, 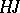
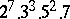
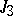 ,
, 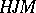
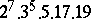
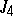
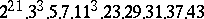
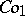 ,
, 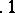
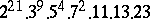
 ,
, 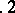

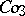 ,
, 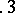
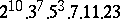
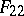 ,
, 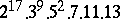
 ,
, 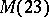
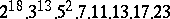
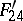 ,
, 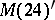
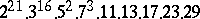

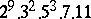
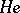 ,
, 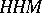
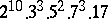
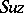

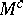
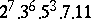
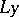
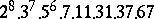
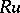
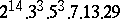
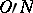 ,
, 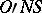
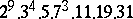
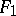 ,
, 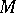
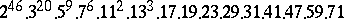
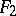 ,
, 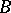
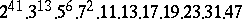
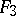 ,
, 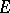 ,
, 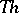
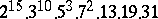
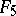 ,
,