Talk:Peano axioms

The Peano axioms page has some problems, stemming (probably) from the its migration to the E of M Wiki-environment.

I noticed the problems while developing the Hilbert 2nd problem page, on which I will be putting a link to the Peano axioms page.

I have done the following:

• reconstructed much of the Peano axioms page using Tex
• added some material that was lost in the migration to E of M
• adjusted some spacing and wording for clarity
• added a few remarks of additional historical interest

There is still an outstanding problem: something is missing on the page with the following text, but I have not yet determined exactly what is missing:

All the axioms are independent, but

and

can be combined to a single one:

The result of my work on this page is shown below. I am loath to change the page before someone has looked at what I my results. Please advise William Hayes (talk) 17:23, 12 June 2015 (CEST)

- - - - -

A system of five axioms for the set of natural numbers $\mathbb{N}$ and a function $S$ (successor) on it, introduced by G. Peano (1889):

1. $0 \in \mathbb{N}$
2. $x \in \mathbb{N} \to Sx \in \mathbb{N}$
3. $x \in \mathbb{N} \to Sx \neq 0$
4. $x \in \mathbb{N} \wedge y \in \mathbb{N} \wedge Sx =Sy \to x = y$
5. $0 \in M \wedge \forall x (x\in M \to Sx\in M) \to \mathbb{N} \subseteq M$ for any property $M$ (axiom of induction).

In the first version of his system, Peano used $1$ instead of $0$ in axioms 1, 3, and 5. Similar axioms were proposed by R. Dedekind (1888).

In the Peano axioms presented above, the axiom of induction (axiom 5) is a statement in second-order language. Dedekind proved that all systems of Peano axioms with such a second-order axiom of induction are categorical. That is, any two systems and satisfying them are isomorphic. The isomorphism is determined by a function , where

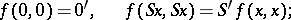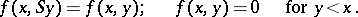The existence of for all pairs and the mutual single-valuedness for are proved by induction.

Peano's axioms make it possible to develop number theory and, in particular, to introduce the usual arithmetic functions and to establish their properties.

All the axioms are independent, but

and

can be combined to a single one:

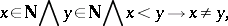if one define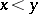s as

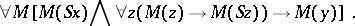The independence of Peano’s axioms is proved by exhibiting, for each axiom, a model for which the axiom considered is false, but for which all the other axioms are true. For example:

• for axiom 1, such a model is the set of natural numbers beginning with $1$
• for axiom 2, it is the set $\mathbb{N} \cup \{1/2\}$, with $S0 = 1/2$ and $S1/2 =1$
• for axiom 3, it is the set $\{0\}$
• for axiom 4, it is the set $\{0, 1\}$, with $S0 = S1 = 1$
• for axiom 5, it is the set $\mathbb{N} \cup \{-1\}$

Using this method, Peano provided a proof of independence for his axioms (1891).

Sometimes one understands by the term Peano arithmetic the system in the first-order language

with the function symbols

$S, +, \cdot$, ::consisting of axioms ::::$Sx\neq 0$ and $Sx = Sy \to x = y$ ::defining equalities for $+$ and $\cdot$ ::::$x + 0 = x$ and $x + Sx = S(x + y)$ ::::$x \cdot 0 = 0$ and $x \cdot S(y) = x \cdot y + x$ ::and with the induction scheme ::::$A (0) \wedge \forall x (A(x) \to A(Sx)) \to \forall x A(x)$ where $A$ is an arbitrary formula, known as the induction formula (see [[Arithmetic, formal|Arithmetic, formal]]). ===='"`UNIQ--h-0--QINU`"'References==== * S.C. Kleene, ''Introduction to Metamathematics'', North-Holland (1951). ===='"`UNIQ--h-1--QINU`"'Comments==== The system of Peano arithmetic in first-order language, mentioned at the end of the article, is no longer categorical (cf. also [[Categoric system of axioms|Categoric system of axioms]]), and gives rise to so-called non-standard models of arithmetic. ===='"`UNIQ--h-2--QINU`"'References==== * H.C. Kennedy, ‘’Peano. Life and works of Giuseppe Peano’’, Reidel (1980). * H.C. Kennedy, ‘’Selected works of Giuseppe Peano’’, Allen & Unwin (1973). * E. Landau, ‘’Grundlagen der Analysis’’, Akad. Verlagsgesellschaft (1930). =='"`UNIQ--h-3--QINU`"' Remark(s) == "Dedekind proved that all systems of Peano axioms with such a second-order axiom of induction are categorical. " — As for me, there is just one "system of Peano axioms" (and it is written above in full, 1-5), and this system of axioms is categorical (that is, all its models are mutually isomorphic). [[User:Boris Tsirelson|Boris Tsirelson]] ([[User talk:Boris Tsirelson|talk]]) 18:52, 12 June 2015 (CEST) Apparently systems of Peano arithmetic axiomatized with a second-order axiom of induction are categorical, but systems of Peano arithmetic axiomatized with a first-order axiom of induction allow for both standard and non-standard models. The first-order induction axiom has the effect of producing a "weaker" system overall, with the result that its models are not all isomorphic. Here's a link to [http://www.xamuel.com/the-axioms-of-peano-arithmetic-modern-version/ First-Order Axioms of Peano Arithmetic] "The isomorphism is determined by a function $f(x,y)$" — I am puzzled. Why not $f(x)$? True, this is written in the article, and still, I do not understand, how does it correspond to the notion of [[isomorphism]]. Do you? [[User:Boris Tsirelson|Boris Tsirelson]] ([[User talk:Boris Tsirelson|talk]]) 19:00, 12 June 2015 (CEST) I must look at this, but feel that I may be over my head. Except for translating to TEX, I have left most of the formalizations as they were in the original article, hoping that the author knew what he was talking about! :-) "for axiom 1, such a model is the set of natural numbers beginning with 1" — Really? What about the occurrence of "0" in axiom 5? [[User:Boris Tsirelson|Boris Tsirelson]] ([[User talk:Boris Tsirelson|talk]]) 19:09, 12 June 2015 (CEST) Yes, there is $0$ in axiom 5, but that $0$ is said to be in set $M$.. Hence, $S0$ is also in set $M$. But neither $0$ nor $S0$ are in $\{1, 2,3, ...\}$. So $\mathbb{N} \subseteq M$ and hence axiom 5 is true, but axiom 1 is false. [[User:Whayes43|William Hayes]] ([[User talk:Whayes43|talk]]) 03:03, 13 June 2015 (CEST) "for axiom 5, it is the set $\mathbb{N} \cup \{-1\}$" — Really? What about $S(-1)$? [[User:Boris Tsirelson|Boris Tsirelson]] ([[User talk:Boris Tsirelson|talk]]) 19:14, 12 June 2015 (CEST) Ah, I assume that whoever constructed the example intended that $S-1 = 0$. This makes axiom 5 false, but not axiom 2 (for example) since $-1$ is not in $\mathbb{N}$. William Hayes (talk) 03:03, 13 June 2015 (CEST)