Difference between revisions of "Talk:Ill-posed problems"
(copied to discussion for TeXing) |
|||
| Line 7: | Line 7: | ||
The concept of a well-posed problem is due to J. Hadamard (1923), who took the point of view that every mathematical problem corresponding to some physical or technological problem must be well-posed. In fact, what physical interpretation can a solution have if an arbitrary small change in the data can lead to large changes in the solution? Moreover, it would be difficult to apply approximation methods to such problems. This put the expediency of studying ill-posed problems in doubt. | The concept of a well-posed problem is due to J. Hadamard (1923), who took the point of view that every mathematical problem corresponding to some physical or technological problem must be well-posed. In fact, what physical interpretation can a solution have if an arbitrary small change in the data can lead to large changes in the solution? Moreover, it would be difficult to apply approximation methods to such problems. This put the expediency of studying ill-posed problems in doubt. | ||
| − | However, this point of view, which is natural when applied to certain time-depended phenomena, cannot be extended to all problems. The following problems are unstable in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012018.png" />, and therefore ill-posed: the solution of integral equations of the first kind; differentiation of functions known only approximately; numerical summation of Fourier series when their coefficients are known approximately in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012019.png" />; the Cauchy problem for the Laplace equation; the problem of analytic continuation of functions; and the inverse problem in gravimetry. Other ill-posed problems are the solution of systems of linear algebraic equations when the system is ill-conditioned; the minimization of functionals having non-convergent minimizing sequences; various problems in linear programming and optimal control; design of optimal systems and optimization of constructions (synthesis problems for antennas and other physical systems); and various other control problems described by differential equations (in particular, differential games). Various physical and technological questions lead to the problems listed (see | + | However, this point of view, which is natural when applied to certain time-depended phenomena, cannot be extended to all problems. The following problems are unstable in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012018.png" />, and therefore ill-posed: the solution of integral equations of the first kind; differentiation of functions known only approximately; numerical summation of Fourier series when their coefficients are known approximately in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012019.png" />; the Cauchy problem for the Laplace equation; the problem of analytic continuation of functions; and the inverse problem in gravimetry. Other ill-posed problems are the solution of systems of linear algebraic equations when the system is ill-conditioned; the minimization of functionals having non-convergent minimizing sequences; various problems in linear programming and optimal control; design of optimal systems and optimization of constructions (synthesis problems for antennas and other physical systems); and various other control problems described by differential equations (in particular, differential games). Various physical and technological questions lead to the problems listed (see {{Cite|TiArAr}}). |
A broad class of so-called inverse problems that arise in physics, technology and other branches of science, in particular, problems of data processing of physical experiments, belongs to the class of ill-posed problems. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012020.png" /> be a characteristic quantity of the phenomenon (or object) to be studied. In a physical experiment the quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012021.png" /> is frequently inaccessible to direct measurement, but what is measured is a certain transform <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012022.png" /> (also called outcome). For the interpretation of the results it is necessary to determine <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012023.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012024.png" />, that is, to solve the equation | A broad class of so-called inverse problems that arise in physics, technology and other branches of science, in particular, problems of data processing of physical experiments, belongs to the class of ill-posed problems. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012020.png" /> be a characteristic quantity of the phenomenon (or object) to be studied. In a physical experiment the quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012021.png" /> is frequently inaccessible to direct measurement, but what is measured is a certain transform <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012022.png" /> (also called outcome). For the interpretation of the results it is necessary to determine <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012023.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012024.png" />, that is, to solve the equation | ||
| Line 28: | Line 28: | ||
==Numerical methods for solving ill-posed problems.== | ==Numerical methods for solving ill-posed problems.== | ||
| − | For ill-posed problems of the form (1) the question arises: What is meant by an approximate solution? Clearly, it should be so defined that it is stable under small changes of the original information. A second question is: What algorithms are there for the construction of such solutions? Answers to these basic questions were given by A.N. Tikhonov (see | + | For ill-posed problems of the form (1) the question arises: What is meant by an approximate solution? Clearly, it should be so defined that it is stable under small changes of the original information. A second question is: What algorithms are there for the construction of such solutions? Answers to these basic questions were given by A.N. Tikhonov (see {{Cite|Ti}}, {{Cite|Ti2}}). |
The selection method. In some cases an approximate solution of (1) can be found by the selection method. It consists of the following: From the class of possible solutions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012053.png" /> one selects an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012054.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012055.png" /> approximates the right-hand side of (1) with required accuracy. For the desired approximate solution one takes the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012056.png" />. The question arises: When is this method applicable, that is, when does | The selection method. In some cases an approximate solution of (1) can be found by the selection method. It consists of the following: From the class of possible solutions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012053.png" /> one selects an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012054.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012055.png" /> approximates the right-hand side of (1) with required accuracy. For the desired approximate solution one takes the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012056.png" />. The question arises: When is this method applicable, that is, when does | ||
| Line 38: | Line 38: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012058.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012058.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012059.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012060.png" />? This holds under the conditions that the solution of (1) is unique and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012061.png" /> is compact (see | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012059.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012060.png" />? This holds under the conditions that the solution of (1) is unique and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012061.png" /> is compact (see {{Cite|Ti3}}). On the basis of these arguments one has formulated the concept (or the condition) of being Tikhonov well-posed, also called conditionally well-posed (see {{Cite|LaLa}}). As applied to (1), a problem is said to be conditionally well-posed if it is known that for the exact value of the right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012062.png" /> there exists a unique solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012063.png" /> of (1) belonging to a given compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012064.png" />. In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012065.png" /> is continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012066.png" />, and if instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012067.png" /> an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012068.png" /> is known such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012070.png" />, then as an approximate solution of (1) with right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012071.png" /> one can take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012072.png" />. As <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012073.png" />, <img al |
ign="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012074.png" /> tends to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012075.png" />. | ign="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012074.png" /> tends to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012075.png" />. | ||
| − | In many cases the approximately known right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012076.png" /> does not belong to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012077.png" />. Under these conditions equation (1) does not have a classical solution. As an approximate solution one takes then a generalized solution, a so-called quasi-solution (see | + | In many cases the approximately known right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012076.png" /> does not belong to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012077.png" />. Under these conditions equation (1) does not have a classical solution. As an approximate solution one takes then a generalized solution, a so-called quasi-solution (see {{Cite|Iv}}). A quasi-solution of (1) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012078.png" /> is an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012079.png" /> that minimizes for a given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012080.png" /> the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012081.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012082.png" /> (see {{Cite|Iv2}}). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012083.png" /> is compact, then a quasi-solution exist for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012084.png" />, and if in addition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012085.png" />, then a quasi-solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012086.png" /> coincides with the classical (exact) solution of (1). The existence of quasi-solutions is guaranteed only when the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012087.png" /> of possible solutions is compact. |
The regularization method. For a number of applied problems leading to (1) a typical situation is that the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012088.png" /> of possible solutions is not compact, the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012089.png" /> is not continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012090.png" />, and changes of the right-hand side of (1) connected with the approximate character can cause the solution to go out of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012091.png" />. Such problems are called essentially ill-posed. An approach has been worked out to solve ill-posed problems that makes it possible to construct numerical methods that approximate solutions of essentially ill-posed problems of the form (1) which are stable under small changes of the data. In this context, both the right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012092.png" /> and the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012093.png" /> should be among the data. | The regularization method. For a number of applied problems leading to (1) a typical situation is that the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012088.png" /> of possible solutions is not compact, the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012089.png" /> is not continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012090.png" />, and changes of the right-hand side of (1) connected with the approximate character can cause the solution to go out of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012091.png" />. Such problems are called essentially ill-posed. An approach has been worked out to solve ill-posed problems that makes it possible to construct numerical methods that approximate solutions of essentially ill-posed problems of the form (1) which are stable under small changes of the data. In this context, both the right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012092.png" /> and the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012093.png" /> should be among the data. | ||
| − | In what follows, for simplicity of exposition it is assumed that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012094.png" /> is known exactly. At the basis of the approach lies the concept of a regularizing operator (see | + | In what follows, for simplicity of exposition it is assumed that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012094.png" /> is known exactly. At the basis of the approach lies the concept of a regularizing operator (see {{Cite|Ti2}}, {{Cite|TiArAr}}). An operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012095.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012096.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012097.png" /> is said to be a regularizing operator for the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012098.png" /> (in a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i05012099.png" />) if it has the following properties: 1) there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120100.png" /> such that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120101.png" /> is defined for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120102.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120103.png" />, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120104.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120105.png" />; and 2) for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120106.png" /> there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120107.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120108.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120109.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120110.png" />. |
Sometimes it is convenient to use another definition of a regularizing operator, comprising the previous one. An operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120111.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120112.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120113.png" />, depending on a parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120114.png" />, is said to be a regularizing operator (or regularization operator) for the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120115.png" /> (in a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120116.png" />) if it has the following properties: 1) there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120117.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120118.png" /> is defined for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120119.png" /> and any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120120.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120121.png" />; and 2) there exists a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120122.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120123.png" /> such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120124.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120125.png" /> such that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120126.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120127.png" />, then <img align="absmiddle" border | Sometimes it is convenient to use another definition of a regularizing operator, comprising the previous one. An operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120111.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120112.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120113.png" />, depending on a parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120114.png" />, is said to be a regularizing operator (or regularization operator) for the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120115.png" /> (in a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120116.png" />) if it has the following properties: 1) there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120117.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120118.png" /> is defined for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120119.png" /> and any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120120.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120121.png" />; and 2) there exists a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120122.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120123.png" /> such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120124.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120125.png" /> such that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120126.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120127.png" />, then <img align="absmiddle" border | ||
="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120128.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120129.png" />. In this definition it is not assumed that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120130.png" /> is globally single-valued. | ="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120128.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120129.png" />. In this definition it is not assumed that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120130.png" /> is globally single-valued. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120131.png" />, then as an approximate solution of (1) with an approximately known right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120132.png" /> one can take the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120133.png" /> obtained by means of the regularizing operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120134.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120135.png" /> is compatible with the error of the initial data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120136.png" /> (see | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120131.png" />, then as an approximate solution of (1) with an approximately known right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120132.png" /> one can take the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120133.png" /> obtained by means of the regularizing operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120134.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120135.png" /> is compatible with the error of the initial data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120136.png" /> (see {{Cite|Ti}}, {{Cite|Ti2}}, {{Cite|TiArAr}}). This is said to be a regularized solution of (1). The numerical parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120137.png" /> is called the regularization parameter. As <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120138.png" />, the regularized approximate solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120139.png" /> tends (in the metric of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120140.png" />) to the exact solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120141.png" />. |
Thus, the task of finding approximate solutions of (1) that are stable under small changes of the right-hand side reduces to: a) finding a regularizing operator; and b) determining the regularization parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120142.png" /> from additional information on the problem, for example, the size of the error with which the right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120143.png" /> is given. | Thus, the task of finding approximate solutions of (1) that are stable under small changes of the right-hand side reduces to: a) finding a regularizing operator; and b) determining the regularization parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120142.png" /> from additional information on the problem, for example, the size of the error with which the right-hand side <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120143.png" /> is given. | ||
The construction of regularizing operators. It is assumed that the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120144.png" /> has a unique solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120145.png" />. Suppose that instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120146.png" /> the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120147.png" /> is solved and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120148.png" />. Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120149.png" />, the approximate solution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120150.png" /> is looked for in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120151.png" /> of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120152.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120153.png" />. This <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120154.png" /> is the set of possible solutions. As an approximate solution one cannot take an arbitrary element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120155.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120156.png" />, since such a "solution" is not unique and is, generally speaking, not continuous in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120157.png" />. As a selection principle for the possible solutions ensuring that one obtains an element (or elements) from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120158.png" /> depending continuously on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120159.png" /> a | The construction of regularizing operators. It is assumed that the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120144.png" /> has a unique solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120145.png" />. Suppose that instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120146.png" /> the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120147.png" /> is solved and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120148.png" />. Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120149.png" />, the approximate solution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120150.png" /> is looked for in the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120151.png" /> of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120152.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120153.png" />. This <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120154.png" /> is the set of possible solutions. As an approximate solution one cannot take an arbitrary element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120155.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120156.png" />, since such a "solution" is not unique and is, generally speaking, not continuous in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120157.png" />. As a selection principle for the possible solutions ensuring that one obtains an element (or elements) from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120158.png" /> depending continuously on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120159.png" /> a | ||
| − | nd tending to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120160.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120161.png" />, one uses the so-called variational principle (see | + | nd tending to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120160.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120161.png" />, one uses the so-called variational principle (see {{Cite|Ti}}). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120162.png" /> be a continuous non-negative functional defined on a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120163.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120164.png" /> that is everywhere-dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120165.png" /> and is such that: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120166.png" />; and b) for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120167.png" /> the set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120168.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120169.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120170.png" />, is compact in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120171.png" />. Functionals having these properties are said to be stabilizing functionals for problem (1). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120172.png" /> be a stabilizing functional defined on a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120173.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120174.png" />. (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120175.png" /> can be the whole of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120176.png" />.) Among the elements of <img align="absmid |
| − | dle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120177.png" /> one looks for one (or several) that minimize(s) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120178.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120179.png" />. The existence of such an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120180.png" /> can be proved (see | + | dle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120177.png" /> one looks for one (or several) that minimize(s) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120178.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120179.png" />. The existence of such an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120180.png" /> can be proved (see {{Cite|TiArAr}}). It can be regarded as the result of applying a certain operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120181.png" /> to the right-hand side of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120182.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120183.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120184.png" /> is a regularizing operator for equation (1). In practice the search for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120185.png" /> can be carried out in the following manner: under mild additional restrictions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120186.png" /> (quasi-monotonicity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120187.png" />, see {{Cite|TiArAr}}) it can be proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120188.png" /> is attained on elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120189.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120190.png" />. An element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120191.png" /> is a solution to the problem of minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120192.png" /> given <img align="absmiddle" bor |
der="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120193.png" />, that is, a solution of a problem of conditional extrema, which can be solved using Lagrange's multiplier method and minimization of the functional | der="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120193.png" />, that is, a solution of a problem of conditional extrema, which can be solved using Lagrange's multiplier method and minimization of the functional | ||
| Line 62: | Line 62: | ||
For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120195.png" /> one can prove that there is an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120196.png" /> minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120197.png" />. The parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120198.png" /> is determined from the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120199.png" />. If there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120200.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120201.png" />, then the original variational problem is equivalent to that of minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120202.png" />, which can be solved by various methods on a computer (for example, by solving the corresponding Euler equation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120203.png" />). The element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120204.png" /> minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120205.png" /> can be regarded as the result of applying to the right-hand side of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120206.png" /> a certain operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120207.png" /> depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120208.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120209.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120210.png" /> is determined by the discrepancy relation <img align="absmiddle" border="0" src="/legacyima | For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120195.png" /> one can prove that there is an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120196.png" /> minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120197.png" />. The parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120198.png" /> is determined from the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120199.png" />. If there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120200.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120201.png" />, then the original variational problem is equivalent to that of minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120202.png" />, which can be solved by various methods on a computer (for example, by solving the corresponding Euler equation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120203.png" />). The element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120204.png" /> minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120205.png" /> can be regarded as the result of applying to the right-hand side of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120206.png" /> a certain operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120207.png" /> depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120208.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120209.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120210.png" /> is determined by the discrepancy relation <img align="absmiddle" border="0" src="/legacyima | ||
| − | ges/i/i050/i050120/i050120211.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120212.png" /> is a regularizing operator for (1). Equivalence of the original variational problem with that of finding the minimum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120213.png" /> holds, for example, for linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120214.png" />. For non-linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120215.png" /> this need not be the case (see | + | ges/i/i050/i050120/i050120211.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120212.png" /> is a regularizing operator for (1). Equivalence of the original variational problem with that of finding the minimum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120213.png" /> holds, for example, for linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120214.png" />. For non-linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120215.png" /> this need not be the case (see {{Cite|GoLeYa}}). |
The so-called smoothing functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120216.png" /> can be introduced formally, without connecting it with a conditional extremum problem for the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120217.png" />, and for an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120218.png" /> minimizing it sought on the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120219.png" />. This poses the problem of finding the regularization parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120220.png" /> as a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120221.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120222.png" />, such that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120223.png" /> determining the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120224.png" /> is regularizing for (1). Under certain conditions (for example, when it is known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120225.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120226.png" /> is a linear operator) such a function exists and can be found from the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120227.png" />. There are also other methods for finding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120228.png" />. | The so-called smoothing functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120216.png" /> can be introduced formally, without connecting it with a conditional extremum problem for the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120217.png" />, and for an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120218.png" /> minimizing it sought on the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120219.png" />. This poses the problem of finding the regularization parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120220.png" /> as a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120221.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120222.png" />, such that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120223.png" /> determining the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120224.png" /> is regularizing for (1). Under certain conditions (for example, when it is known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120225.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120226.png" /> is a linear operator) such a function exists and can be found from the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120227.png" />. There are also other methods for finding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120228.png" />. | ||
| Line 71: | Line 71: | ||
Methods for finding the regularization parameter depend on the additional information available on the problem. If the error of the right-hand side of the equation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120250.png" /> is known, say <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120251.png" />, then in accordance with the preceding it is natural to determine <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120252.png" /> by the discrepancy, that is, from the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120253.png" />. | Methods for finding the regularization parameter depend on the additional information available on the problem. If the error of the right-hand side of the equation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120250.png" /> is known, say <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120251.png" />, then in accordance with the preceding it is natural to determine <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120252.png" /> by the discrepancy, that is, from the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120253.png" />. | ||
| − | The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120254.png" /> is monotone and semi-continuous for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120255.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120256.png" /> is a linear operator, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120257.png" /> a Hilbert space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120258.png" /> a strictly-convex functional (for example, quadratic), then the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120259.png" /> is unique and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120260.png" /> is a single-valued function. Under these conditions, for every positive number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120261.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120262.png" />, there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120263.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120264.png" /> (see | + | The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120254.png" /> is monotone and semi-continuous for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120255.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120256.png" /> is a linear operator, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120257.png" /> a Hilbert space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120258.png" /> a strictly-convex functional (for example, quadratic), then the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120259.png" /> is unique and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120260.png" /> is a single-valued function. Under these conditions, for every positive number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120261.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120262.png" />, there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120263.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120264.png" /> (see {{Cite|TiArAr}}). |
| − | However, for a non-linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120265.png" /> the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120266.png" /> may have no solution (see | + | However, for a non-linear operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120265.png" /> the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120266.png" /> may have no solution (see {{Cite|GoLeYa}}). |
The regularization method is closely connected with the construction of splines (cf. [[Spline|Spline]]). For example, the problem of finding a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120267.png" /> with piecewise-continuous second-order derivative on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120268.png" /> that minimizes the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120269.png" /> and takes given values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120270.png" /> on a grid <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120271.png" />, is equivalent to the construction of a spline of the second degree. | The regularization method is closely connected with the construction of splines (cf. [[Spline|Spline]]). For example, the problem of finding a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120267.png" /> with piecewise-continuous second-order derivative on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120268.png" /> that minimizes the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120269.png" /> and takes given values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120270.png" /> on a grid <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120271.png" />, is equivalent to the construction of a spline of the second degree. | ||
| − | A regularizing operator can be constructed by spectral methods (see | + | A regularizing operator can be constructed by spectral methods (see {{Cite|TiArAr}}, {{Cite|GoLeYa}}), by means of the classical integral transforms in the case of equations of convolution type (see {{Cite|Ar}}, {{Cite|TiArAr}}), by the method of quasi-mappings (see {{Cite|LaLi}}), or by the iteration method (see {{Cite|Kr}}). Necessary and sufficient conditions for the existence of a regularizing operator are known (see {{Cite|Vi}}). |
Next, suppose that not only the right-hand side of (1) but also the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120272.png" /> is given approximately, so that instead of the exact initial data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120273.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120274.png" />, where | Next, suppose that not only the right-hand side of (1) but also the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120272.png" /> is given approximately, so that instead of the exact initial data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120273.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120274.png" />, where | ||
| Line 89: | Line 89: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120278.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120278.png" /></td> </tr></table> | ||
| − | and the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120279.png" /> can be determined, for example, from the relation (see | + | and the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120279.png" /> can be determined, for example, from the relation (see {{Cite|TiArAr}}) |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120280.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120280.png" /></td> </tr></table> | ||
| Line 97: | Line 97: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120284.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120284.png" /></td> </tr></table> | ||
| − | An approximation to a normal solution that is stable under small changes in the right-hand side of (1) can be found by the regularization method described above. The class of problems with infinitely many solutions includes degenerate systems of linear algebraic equations. So-called badly-conditioned systems of linear algebraic equations can be regarded as systems obtained from degenerate ones when the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120285.png" /> is replaced by its approximation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120286.png" />. As a normal solution of a corresponding degenerate system one can take a solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120287.png" /> of minimal norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120288.png" />. In the smoothing functional one can take for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120289.png" /> the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120290.png" />. Approximate solutions of badly-conditioned systems can also be found by the regularization method with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120291.png" /> (see | + | An approximation to a normal solution that is stable under small changes in the right-hand side of (1) can be found by the regularization method described above. The class of problems with infinitely many solutions includes degenerate systems of linear algebraic equations. So-called badly-conditioned systems of linear algebraic equations can be regarded as systems obtained from degenerate ones when the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120285.png" /> is replaced by its approximation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120286.png" />. As a normal solution of a corresponding degenerate system one can take a solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120287.png" /> of minimal norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120288.png" />. In the smoothing functional one can take for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120289.png" /> the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120290.png" />. Approximate solutions of badly-conditioned systems can also be found by the regularization method with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120291.png" /> (see {{Cite|TiArAr}}). |
Similar methods can be used to solve a Fredholm integral equation of the second kind in the spectrum, that is, when the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120292.png" /> of the equation is equal to one of the eigen values of the kernel. | Similar methods can be used to solve a Fredholm integral equation of the second kind in the spectrum, that is, when the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120292.png" /> of the equation is equal to one of the eigen values of the kernel. | ||
| Line 118: | Line 118: | ||
over the argument is stable. | over the argument is stable. | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120324.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120325.png" /> be null-sequences such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120326.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120327.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120328.png" /> be a sequence of elements minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120329.png" />. This is a regularizing minimizing sequence for the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120330.png" /> (see | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120324.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120325.png" /> be null-sequences such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120326.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120327.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120328.png" /> be a sequence of elements minimizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120329.png" />. This is a regularizing minimizing sequence for the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120330.png" /> (see {{Cite|TiArAr}}), consequently, it converges as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120331.png" /> to an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120332.png" />. As approximate solutions of the problems one can then take the elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120333.png" />. |
Similarly approximate solutions of ill-posed problems in optimal control can be constructed. | Similarly approximate solutions of ill-posed problems in optimal control can be constructed. | ||
| − | In applications ill-posed problems often occur where the initial data contain random errors. For the construction of approximate solutions to such classes both deterministic and probability approaches are possible (see | + | In applications ill-posed problems often occur where the initial data contain random errors. For the construction of approximate solutions to such classes both deterministic and probability approaches are possible (see {{Cite|TiArAr}}, {{Cite|LaVa}}). |
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |- | |
| + | | valign="top"|{{Ref|Ar}}||valign="top"| V.Ya. Arsenin, "On a method for obtaining approximate solutions to convolution integral equations of the first kind" ''Proc. Steklov Inst. Math.'', '''133''' (1977) pp. 31–48 ''Trudy Mat. Inst. Steklov.'', '''133''' (1973) pp. 33–51 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ba}}||valign="top"| A.B. Bakushinskii, "A general method for constructing regularizing algorithms for a linear ill-posed equation in Hilbert space" ''USSR Comp. Math. Math. Phys.'', '''7''' : 3 (1968) pp. 279–287 ''Zh. Vychisl. Mat. i Mat. Fiz.'', '''7''' : 3 (1967) pp. 672–677 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|GoLeYa}}||valign="top"| A.V. Goncharskii, A.S. Leonov, A.G. Yagoda, "On the residual principle for solving nonlinear ill-posed problems" ''Soviet Math. Dokl.'', '''15''' (1974) pp. 166–168 ''Dokl. Akad. Nauk SSSR'', '''214''' : 3 (1974) pp. 499–500 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Iv}}||valign="top"| V.K. Ivanov, "On ill-posed problems" ''Mat. Sb.'', '''61''' : 2 (1963) pp. 211–223 (In Russian) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Iv2}}||valign="top"| V.K. Ivanov, "On linear problems which are not well-posed" ''Soviet Math. Dokl.'', '''3''' (1962) pp. 981–983 ''Dokl. Akad. Nauk SSSR'', '''145''' : 2 (1962) pp. 270–272 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Kr}}||valign="top"| A.V. Kryanev, "The solution of incorrectly posed problems by methods of successive approximations" ''Soviet Math. Dokl.'', '''14''' (1973) pp. 673–676 ''Dokl. Akad. Nauk SSSR'', '''210''' : 1 pp. 20–22 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|LaLa}}||valign="top"| M.M. [M.A. Lavrent'ev] Lavrentiev, "Some improperly posed problems of mathematical physics", Springer (1967) (Translated from Russian) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|LaLi}}||valign="top"| R. Lattes, J.L. Lions, "Méthode de quasi-réversibilité et applications", Dunod (1967) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|LaVa}}||valign="top"| M.M. Lavrent'ev, V.G. Vasil'ev, "The posing of certain improper problems of mathematical physics" ''Sib. Math. J.'', '''7''' : 3 (1966) pp. 450–463 ''Sibirsk. Mat. Zh.'', '''7''' : 3 (1966) pp. 559–576 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ti}}||valign="top"| A.N. Tikhonov, "Solution of incorrectly formulated problems and the regularization method" ''Soviet Math. Dokl.'', '''4''' (1963) pp. 1035–1038 ''Dokl. Akad. Nauk SSSR'', '''151''' : 3 (1963) pp. 501–504 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ti2}}||valign="top"| A.N. Tikhonov, "Regularization of incorrectly posed problems" ''Soviet Math. Dokl.'', '''4''' (1963) pp. 1624–1627 ''Dokl. Akad. Nauk SSSR'', '''153''' : 1 (1963) pp. 49–52 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ti3}}||valign="top"| A.N. Tikhonov, "On stability of inverse problems" ''Dokl. Akad. Nauk SSSR'', '''39''' : 5 (1943) pp. 176–179 (In Russian) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ti4}}||valign="top"| A.N. Tikhonov, "On the stability of the functional optimization problem" ''USSR Comp. Math. Math. Phys.'', '''6''' : 4 (1966) pp. 28–33 ''Zh. Vychisl. Mat. i Mat. Fiz.'', '''6''' : 4 (1966) pp. 631–634 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|TiArAr}}||valign="top"| A.N. Tikhonov, V.I. [V.I. Arsenin] Arsenine, "Solution of ill-posed problems", Winston (1977) (Translated from Russian) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Vi}}||valign="top"| V.A. Vinokurov, "On the regularization of discontinuous mappings" ''USSR Comp. Math. Math. Phys.'', '''11''' : 5 (1971) pp. 1–21 ''Zh. Vychisl. Mat. i Mat. Fiz.'', '''11''' : 5 (1971) pp. 1097–1112 | ||
| + | |- | ||
| + | |} | ||
| + | |||
====Comments==== | ====Comments==== | ||
| − | The idea of conditional well-posedness was also found by B.L. Phillips | + | The idea of conditional well-posedness was also found by B.L. Phillips {{Cite|Ph}}; the expression "Tikhonov well-posed" is not used in the West. |
| − | Other problems that lead to ill-posed problems in the sense described above are the [[Dirichlet problem|Dirichlet problem]] for the wave equation, the non-characteristic [[Cauchy problem|Cauchy problem]] for the heat equation, the initial boundary value problem for the backward [[Heat equation|heat equation]], inverse scattering problems ( | + | Other problems that lead to ill-posed problems in the sense described above are the [[Dirichlet problem|Dirichlet problem]] for the wave equation, the non-characteristic [[Cauchy problem|Cauchy problem]] for the heat equation, the initial boundary value problem for the backward [[Heat equation|heat equation]], inverse scattering problems ({{Cite|CoKr}}), identification of parameters (coefficients) in partial differential equations from over-specified data ({{Cite|Ba2}}, {{Cite|EnGr}}), and computerized tomography ({{Cite|Na2}}). |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120334.png" /> is a bounded linear operator between Hilbert spaces, then, as also mentioned above, regularization operators can be constructed via [[Spectral theory|spectral theory]]: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120335.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120336.png" />, then under mild assumptions, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120337.png" /> is a regularization operator (cf. | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120334.png" /> is a bounded linear operator between Hilbert spaces, then, as also mentioned above, regularization operators can be constructed via [[Spectral theory|spectral theory]]: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120335.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120336.png" />, then under mild assumptions, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120337.png" /> is a regularization operator (cf. {{Cite|Gr}}); for choices of the regularization parameter leading to optimal convergence rates for such methods see {{Cite|EnGf}}. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120338.png" />, the resulting method is called Tikhonov regularization: The regularized solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120339.png" /> is defined via <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120340.png" />. A variant of this method in Hilbert scales has been developed in {{Cite|Na}} with parameter choice rules given in {{Cite|Ne}}. The parameter choice rule discussed in the article given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050120/i050120341.png" /> is called the discrepancy principle ({{Cite|Mo}}). |
====References==== | ====References==== | ||
| − | + | {| | |
| − | some radiological applications" ''J. Appl. Phys.'' , '''34''' (1963) | + | |- |
| − | + | | valign="top"|{{Ref|Ba2}}||valign="top"| J. Baumeister, "Stable solution of inverse problems", Vieweg (1986) | |
| + | |- | ||
| + | | valign="top"|{{Ref|Ba3}}||valign="top"| H.P. Baltes (ed.), ''Inverse source problems in optics'', Springer (1978) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ba4}}||valign="top"| H.P. Baltes (ed.), ''Inverse scattering problems in optics'', Springer (1980) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|BaGi}}||valign="top"| G. Backus, F. Gilbert, "The resolving power of gross earth data" ''Geophys. J. R. Astr. Soc.'', '''16''' (1968) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|BeBlSt}}||valign="top"| J.V. Beck, B. Blackwell, C.R. StClair, "Inverse heat conduction: ill posed problems", Wiley (1985) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|BoJo}}||valign="top"| W.M. Boerner, A.K. (eds.) Jordan, "Inverse methods in electromagnetics" ''IEEE Trans. Antennas Propag.'', '''2''' (1981) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ca}}||valign="top"| J.R. Cann on, "The one-dimensional heat equation", Addison-Wesley (1984) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|CaSt}}||valign="top"| A. Carasso, A.P. Stone, "Improperly posed boundary value problems", Pitman (1975) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Co}}||valign="top"| A.M. Cormak, "Representation of a function by its line integrals with some radiological applications" ''J. Appl. Phys.'', '''34''' (1963) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Co2}}||valign="top"| L. Colin, "Mathematics of profile inversion", ''Proc. Workshop Ames Res. Center, June 12–16, 1971'', '''TM-X-62.150''', NASA | ||
| + | |- | ||
| + | | valign="top"|{{Ref|CoKr}}||valign="top"| D.L. Colton, R. Kress, "Integral equation methods in scattering theory", Wiley (1983) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|EnGf}}||valign="top"| H.W. Engl, H. Gfrerer, "A posteriori parameter choice for general regularization methods for solving linear ill-posed problems" ''Appl. Num. Math.'', '''4''' (1988) pp. 395–417 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|EnGr}}||valign="top"| H.W. Engl (ed.) C.W. Groetsch (ed.), ''Inverse and ill-posed problems'', Acad. Press (1987) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Gr}}||valign="top"| C.W. Groetsch, "The theory of Tikhonov regularization for Fredholm equations of the first kind", Pitman (1984) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Gr2}}||valign="top"| C.W. Groetsch, "The theory of Tikhonov regularization for Fredholm equations of the first kind", Pitman (1984) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|He}}||valign="top"| G.T. Herman (ed.), ''Image reconstruction from projections'', Springer (1979) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|HeNa}}||valign="top"| G.T. Herman (ed.) F. Natterer (ed.), ''Mathematical aspects of computerized tomography, Proc. Oberwolfach, February 10–16, 1980'', Springer (1981) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Jo}}||valign="top"| F. John, "Continuous dependence on data for solutions of partial differential equations with a prescribed bound" ''Comm. Pure Appl. Math.'', '''13''' (1960) pp. 551–585 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ka}}||valign="top"| M. Kac, "Can one hear the shape of a drum?" ''Amer. Math. Monthly'', '''73''' (1966) pp. 1–23 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|LaRoSh}}||valign="top"| M.H. Lavrent'ev, V.G. Romanov, S.P. Shishalskii, "Ill-posed problems of mathematical physics and analysis", Amer. Math. Soc. (1986) (Translated from Russian) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Mo}}||valign="top"| V.A. Morozov, "Methods for solving incorrectly posed problems", Springer (1984) (Translated from Russian) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Na}}||valign="top"| F. Natterer, "Error bounds for Tikhonov regularization in Hilbert scales" ''Applic. Analysis'', '''18''' (1984) pp. 29–37 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Na2}}||valign="top"| F. Natterer, "The mathematics of computerized tomography", Wiley (1986) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ne}}||valign="top"| A. Neubauer, "An a-posteriori parameter choice for Tikhonov regularization in Hilbert scales leading to optimal convergence rates" ''SIAM J. Numer. Anal.'', '''25''' (1988) pp. 1313–1326 | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Pa}}||valign="top"| L.E. Payne, "Improperly posed problems in partial differential equations", SIAM (1975) | ||
| + | |- | ||
| + | | valign="top"|{{Ref|Ph}}||valign="top"| B.L. Phillips, "A technique for the numerical solution of certain integral equations of the first kind" ''J. ACM'', '''9''' (1962) pp. 84–97 | ||
| + | |- | ||
| + | |} | ||
Revision as of 17:34, 22 April 2012
This is being TeXed by --Jjg 12:29, 22 April 2012 (CEST)
incorrectly-posed problems, improperly-posed problems
Problems for which at least one of the conditions below, which characterize well-posed problems, is violated. The problem of determining a solution 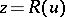 in a metric space
in a metric space 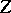 (with metric
(with metric 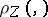 ) from "initial data"
) from "initial data"  in a metric space
in a metric space 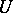 (with metric
(with metric 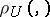 ) is said to be well-posed on the pair of spaces
) is said to be well-posed on the pair of spaces 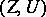 if: a) for every
if: a) for every 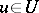 there exists a solution
there exists a solution 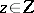 ; b) the solution is uniquely determined; and c) the problem is stable on the spaces
; b) the solution is uniquely determined; and c) the problem is stable on the spaces 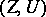 , i.e.: For every
, i.e.: For every 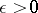 there is a
there is a 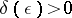 such that for any
such that for any 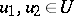 it follows from
it follows from 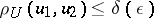 that
that 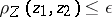 , where
, where 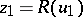 and
and 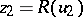 .
.
The concept of a well-posed problem is due to J. Hadamard (1923), who took the point of view that every mathematical problem corresponding to some physical or technological problem must be well-posed. In fact, what physical interpretation can a solution have if an arbitrary small change in the data can lead to large changes in the solution? Moreover, it would be difficult to apply approximation methods to such problems. This put the expediency of studying ill-posed problems in doubt.
However, this point of view, which is natural when applied to certain time-depended phenomena, cannot be extended to all problems. The following problems are unstable in the metric of 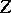 , and therefore ill-posed: the solution of integral equations of the first kind; differentiation of functions known only approximately; numerical summation of Fourier series when their coefficients are known approximately in the metric of
, and therefore ill-posed: the solution of integral equations of the first kind; differentiation of functions known only approximately; numerical summation of Fourier series when their coefficients are known approximately in the metric of 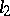 ; the Cauchy problem for the Laplace equation; the problem of analytic continuation of functions; and the inverse problem in gravimetry. Other ill-posed problems are the solution of systems of linear algebraic equations when the system is ill-conditioned; the minimization of functionals having non-convergent minimizing sequences; various problems in linear programming and optimal control; design of optimal systems and optimization of constructions (synthesis problems for antennas and other physical systems); and various other control problems described by differential equations (in particular, differential games). Various physical and technological questions lead to the problems listed (see [TiArAr]).
; the Cauchy problem for the Laplace equation; the problem of analytic continuation of functions; and the inverse problem in gravimetry. Other ill-posed problems are the solution of systems of linear algebraic equations when the system is ill-conditioned; the minimization of functionals having non-convergent minimizing sequences; various problems in linear programming and optimal control; design of optimal systems and optimization of constructions (synthesis problems for antennas and other physical systems); and various other control problems described by differential equations (in particular, differential games). Various physical and technological questions lead to the problems listed (see [TiArAr]).
A broad class of so-called inverse problems that arise in physics, technology and other branches of science, in particular, problems of data processing of physical experiments, belongs to the class of ill-posed problems. Let  be a characteristic quantity of the phenomenon (or object) to be studied. In a physical experiment the quantity
be a characteristic quantity of the phenomenon (or object) to be studied. In a physical experiment the quantity  is frequently inaccessible to direct measurement, but what is measured is a certain transform
is frequently inaccessible to direct measurement, but what is measured is a certain transform 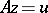 (also called outcome). For the interpretation of the results it is necessary to determine
(also called outcome). For the interpretation of the results it is necessary to determine  from
from  , that is, to solve the equation
, that is, to solve the equation
 | (1) |
Problems of solving an equation (1) are often called pattern recognition problems. Problems leading to the minimization of functionals (design of antennas and other systems or constructions, problems of optimal control and many others) are also called synthesis problems.
Suppose that in a mathematical model for some physical experiments the object to be studied (the phenomenon) is characterized by an element  (a function, a vector) belonging to a set
(a function, a vector) belonging to a set 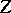 of possible solutions in a metric space
of possible solutions in a metric space 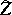 . Suppose that
. Suppose that 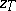 is inaccessible to direct measurement and that what is measured is a transform,
is inaccessible to direct measurement and that what is measured is a transform, 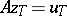 ,
, 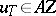 , where
, where 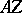 is the image of
is the image of 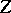 under the operator
under the operator 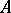 . Evidently,
. Evidently, 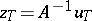 , where
, where 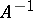 is the operator inverse to
is the operator inverse to 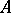 . Since
. Since 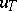 is obtained by measurement, it is known only approximately. Let
is obtained by measurement, it is known only approximately. Let 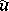 be this approximate value. Under these conditions the question can only be that of finding a "solution" of the equation
be this approximate value. Under these conditions the question can only be that of finding a "solution" of the equation
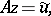 | (2) |
approximating 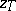 .
.
In many cases the operator 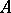 is such that its inverse
is such that its inverse 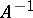 is not continuous, for example, when
is not continuous, for example, when 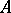 is a completely-continuous operator in a Hilbert space, in particular an integral operator of the form
is a completely-continuous operator in a Hilbert space, in particular an integral operator of the form
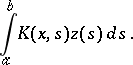 |
Under these conditions one cannot take, following classical ideas, an exact solution of (2), that is, the element 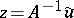 , as an approximate "solution" to
, as an approximate "solution" to 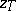 . In fact: a) such a solution need not exist on
. In fact: a) such a solution need not exist on 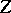 , since
, since 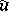 need not belong to
need not belong to 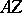 ; and b) such a solution, if it exists, need not be stable under small changes of
; and b) such a solution, if it exists, need not be stable under small changes of 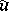 (due to the fact that
(due to the fact that 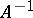 is not continuous) and, consequently, need not have a physical interpretation. The problem (2) then is ill-posed.
is not continuous) and, consequently, need not have a physical interpretation. The problem (2) then is ill-posed.
Numerical methods for solving ill-posed problems.
For ill-posed problems of the form (1) the question arises: What is meant by an approximate solution? Clearly, it should be so defined that it is stable under small changes of the original information. A second question is: What algorithms are there for the construction of such solutions? Answers to these basic questions were given by A.N. Tikhonov (see [Ti], [Ti2]).
The selection method. In some cases an approximate solution of (1) can be found by the selection method. It consists of the following: From the class of possible solutions 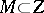 one selects an element
one selects an element 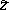 for which
for which 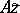 approximates the right-hand side of (1) with required accuracy. For the desired approximate solution one takes the element
approximates the right-hand side of (1) with required accuracy. For the desired approximate solution one takes the element 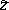 . The question arises: When is this method applicable, that is, when does
. The question arises: When is this method applicable, that is, when does
 |
imply that
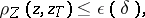 |
where 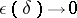 as
as 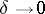 ? This holds under the conditions that the solution of (1) is unique and that
? This holds under the conditions that the solution of (1) is unique and that 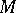 is compact (see [Ti3]). On the basis of these arguments one has formulated the concept (or the condition) of being Tikhonov well-posed, also called conditionally well-posed (see [LaLa]). As applied to (1), a problem is said to be conditionally well-posed if it is known that for the exact value of the right-hand side
is compact (see [Ti3]). On the basis of these arguments one has formulated the concept (or the condition) of being Tikhonov well-posed, also called conditionally well-posed (see [LaLa]). As applied to (1), a problem is said to be conditionally well-posed if it is known that for the exact value of the right-hand side 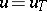 there exists a unique solution
there exists a unique solution 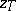 of (1) belonging to a given compact set
of (1) belonging to a given compact set 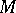 . In this case
. In this case 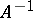 is continuous on
is continuous on 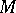 , and if instead of
, and if instead of 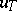 an element
an element 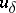 is known such that
is known such that 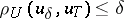 and
and 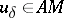 , then as an approximate solution of (1) with right-hand side
, then as an approximate solution of (1) with right-hand side 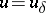 one can take
one can take 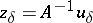 . As
. As 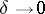 ,
, 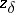 tends to
tends to 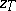 .
.
In many cases the approximately known right-hand side 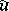 does not belong to
does not belong to 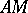 . Under these conditions equation (1) does not have a classical solution. As an approximate solution one takes then a generalized solution, a so-called quasi-solution (see [Iv]). A quasi-solution of (1) on
. Under these conditions equation (1) does not have a classical solution. As an approximate solution one takes then a generalized solution, a so-called quasi-solution (see [Iv]). A quasi-solution of (1) on 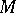 is an element
is an element 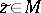 that minimizes for a given
that minimizes for a given 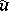 the functional
the functional 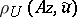 on
on 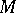 (see [Iv2]). If
(see [Iv2]). If 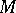 is compact, then a quasi-solution exist for any
is compact, then a quasi-solution exist for any 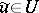 , and if in addition
, and if in addition 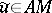 , then a quasi-solution
, then a quasi-solution 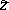 coincides with the classical (exact) solution of (1). The existence of quasi-solutions is guaranteed only when the set
coincides with the classical (exact) solution of (1). The existence of quasi-solutions is guaranteed only when the set 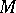 of possible solutions is compact.
of possible solutions is compact.
The regularization method. For a number of applied problems leading to (1) a typical situation is that the set 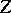 of possible solutions is not compact, the operator
of possible solutions is not compact, the operator  is not continuous on
is not continuous on 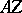 , and changes of the right-hand side of (1) connected with the approximate character can cause the solution to go out of
, and changes of the right-hand side of (1) connected with the approximate character can cause the solution to go out of 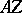 . Such problems are called essentially ill-posed. An approach has been worked out to solve ill-posed problems that makes it possible to construct numerical methods that approximate solutions of essentially ill-posed problems of the form (1) which are stable under small changes of the data. In this context, both the right-hand side
. Such problems are called essentially ill-posed. An approach has been worked out to solve ill-posed problems that makes it possible to construct numerical methods that approximate solutions of essentially ill-posed problems of the form (1) which are stable under small changes of the data. In this context, both the right-hand side  and the operator
and the operator 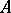 should be among the data.
should be among the data.
In what follows, for simplicity of exposition it is assumed that the operator 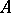 is known exactly. At the basis of the approach lies the concept of a regularizing operator (see [Ti2], [TiArAr]). An operator
is known exactly. At the basis of the approach lies the concept of a regularizing operator (see [Ti2], [TiArAr]). An operator 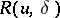 from
from  to
to 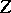 is said to be a regularizing operator for the equation
is said to be a regularizing operator for the equation 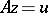 (in a neighbourhood of
(in a neighbourhood of 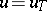 ) if it has the following properties: 1) there exists a
) if it has the following properties: 1) there exists a 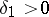 such that the operator
such that the operator 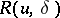 is defined for every
is defined for every 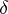 ,
, 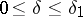 , and for any
, and for any 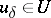 such that
such that 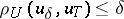 ; and 2) for every
; and 2) for every 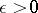 there exists a
there exists a 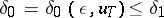 such that
such that 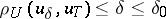 implies
implies 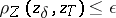 , where
, where 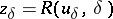 .
.
Sometimes it is convenient to use another definition of a regularizing operator, comprising the previous one. An operator 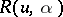 from
from 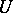 to
to 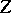 , depending on a parameter
, depending on a parameter 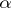 , is said to be a regularizing operator (or regularization operator) for the equation
, is said to be a regularizing operator (or regularization operator) for the equation 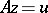 (in a neighbourhood of
(in a neighbourhood of 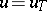 ) if it has the following properties: 1) there exists a
) if it has the following properties: 1) there exists a 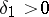 such that
such that 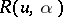 is defined for every
is defined for every 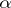 and any
and any 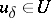 for which
for which 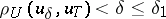 ; and 2) there exists a function
; and 2) there exists a function 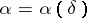 of
of 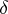 such that for any
such that for any 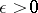 there is a
there is a 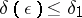 such that if
such that if 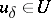 and
and 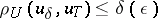 , then
, then 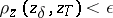 , where
, where 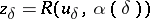 . In this definition it is not assumed that the operator
. In this definition it is not assumed that the operator 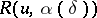 is globally single-valued.
is globally single-valued.
If 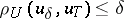 , then as an approximate solution of (1) with an approximately known right-hand side
, then as an approximate solution of (1) with an approximately known right-hand side 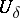 one can take the element
one can take the element 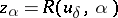 obtained by means of the regularizing operator
obtained by means of the regularizing operator 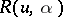 , where
, where 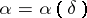 is compatible with the error of the initial data
is compatible with the error of the initial data 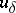 (see [Ti], [Ti2], [TiArAr]). This is said to be a regularized solution of (1). The numerical parameter
(see [Ti], [Ti2], [TiArAr]). This is said to be a regularized solution of (1). The numerical parameter 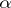 is called the regularization parameter. As
is called the regularization parameter. As 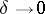 , the regularized approximate solution
, the regularized approximate solution 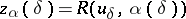 tends (in the metric of
tends (in the metric of 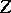 ) to the exact solution
) to the exact solution 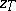 .
.
Thus, the task of finding approximate solutions of (1) that are stable under small changes of the right-hand side reduces to: a) finding a regularizing operator; and b) determining the regularization parameter 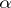 from additional information on the problem, for example, the size of the error with which the right-hand side
from additional information on the problem, for example, the size of the error with which the right-hand side  is given.
is given.
The construction of regularizing operators. It is assumed that the equation 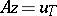 has a unique solution
has a unique solution 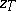 . Suppose that instead of
. Suppose that instead of 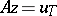 the equation
the equation 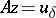 is solved and that
is solved and that 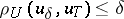 . Since
. Since 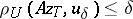 , the approximate solution of
, the approximate solution of 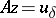 is looked for in the class
is looked for in the class 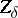 of elements
of elements 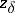 such that
such that 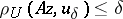 . This
. This 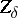 is the set of possible solutions. As an approximate solution one cannot take an arbitrary element
is the set of possible solutions. As an approximate solution one cannot take an arbitrary element 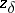 from
from 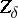 , since such a "solution" is not unique and is, generally speaking, not continuous in
, since such a "solution" is not unique and is, generally speaking, not continuous in 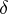 . As a selection principle for the possible solutions ensuring that one obtains an element (or elements) from
. As a selection principle for the possible solutions ensuring that one obtains an element (or elements) from 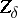 depending continuously on
depending continuously on 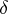 a
nd tending to
a
nd tending to 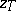 as
as 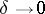 , one uses the so-called variational principle (see [Ti]). Let
, one uses the so-called variational principle (see [Ti]). Let 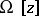 be a continuous non-negative functional defined on a subset
be a continuous non-negative functional defined on a subset 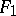 of
of 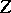 that is everywhere-dense in
that is everywhere-dense in 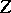 and is such that: a)
and is such that: a) 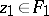 ; and b) for every
; and b) for every 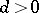 the set of elements
the set of elements  in
in 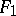 for which
for which 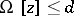 , is compact in
, is compact in 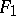 . Functionals having these properties are said to be stabilizing functionals for problem (1). Let
. Functionals having these properties are said to be stabilizing functionals for problem (1). Let 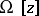 be a stabilizing functional defined on a subset
be a stabilizing functional defined on a subset 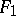 of
of 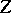 . (
. (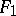 can be the whole of
can be the whole of 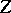 .) Among the elements of
.) Among the elements of 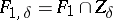 one looks for one (or several) that minimize(s)
one looks for one (or several) that minimize(s) 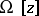 on
on 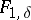 . The existence of such an element
. The existence of such an element 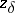 can be proved (see [TiArAr]). It can be regarded as the result of applying a certain operator
can be proved (see [TiArAr]). It can be regarded as the result of applying a certain operator 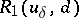 to the right-hand side of the equation
to the right-hand side of the equation 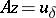 , that is,
, that is, 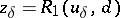 . Then
. Then 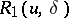 is a regularizing operator for equation (1). In practice the search for
is a regularizing operator for equation (1). In practice the search for 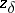 can be carried out in the following manner: under mild additional restrictions on
can be carried out in the following manner: under mild additional restrictions on 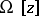 (quasi-monotonicity of
(quasi-monotonicity of 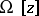 , see [TiArAr]) it can be proved that
, see [TiArAr]) it can be proved that 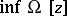 is attained on elements
is attained on elements 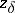 for which
for which 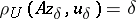 . An element
. An element 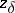 is a solution to the problem of minimizing
is a solution to the problem of minimizing 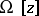 given
given 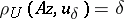 , that is, a solution of a problem of conditional extrema, which can be solved using Lagrange's multiplier method and minimization of the functional
, that is, a solution of a problem of conditional extrema, which can be solved using Lagrange's multiplier method and minimization of the functional
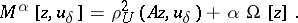 |
For any 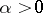 one can prove that there is an element
one can prove that there is an element 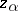 minimizing
minimizing 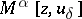 . The parameter
. The parameter 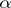 is determined from the condition
is determined from the condition 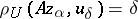 . If there is an
. If there is an 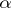 for which
for which 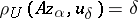 , then the original variational problem is equivalent to that of minimizing
, then the original variational problem is equivalent to that of minimizing 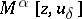 , which can be solved by various methods on a computer (for example, by solving the corresponding Euler equation for
, which can be solved by various methods on a computer (for example, by solving the corresponding Euler equation for 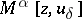 ). The element
). The element 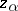 minimizing
minimizing 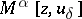 can be regarded as the result of applying to the right-hand side of the equation
can be regarded as the result of applying to the right-hand side of the equation 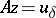 a certain operator
a certain operator 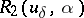 depending on
depending on 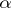 , that is,
, that is, 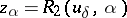 in which
in which 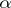 is determined by the discrepancy relation
is determined by the discrepancy relation . Then
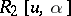 is a regularizing operator for (1). Equivalence of the original variational problem with that of finding the minimum of
is a regularizing operator for (1). Equivalence of the original variational problem with that of finding the minimum of 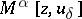 holds, for example, for linear operators
holds, for example, for linear operators 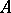 . For non-linear operators
. For non-linear operators 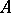 this need not be the case (see [GoLeYa]).
this need not be the case (see [GoLeYa]).
The so-called smoothing functional 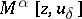 can be introduced formally, without connecting it with a conditional extremum problem for the functional
can be introduced formally, without connecting it with a conditional extremum problem for the functional 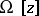 , and for an element
, and for an element 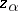 minimizing it sought on the set
minimizing it sought on the set 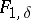 . This poses the problem of finding the regularization parameter
. This poses the problem of finding the regularization parameter 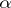 as a function of
as a function of 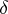 ,
, 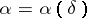 , such that the operator
, such that the operator 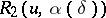 determining the element
determining the element 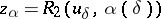 is regularizing for (1). Under certain conditions (for example, when it is known that
is regularizing for (1). Under certain conditions (for example, when it is known that 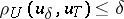 and
and 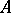 is a linear operator) such a function exists and can be found from the relation
is a linear operator) such a function exists and can be found from the relation  . There are also other methods for finding
. There are also other methods for finding 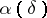 .
.
Let 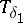 be a class of non-negative non-decreasing continuous functions on
be a class of non-negative non-decreasing continuous functions on 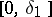 ,
, 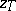 a solution of (1) with right-hand side
a solution of (1) with right-hand side 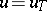 , and
, and 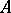 a continuous operator from
a continuous operator from 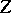 to
to 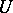 . For any positive number
. For any positive number  and functions
and functions 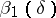 and
and 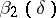 from
from 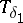 such that
such that 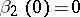 and
and 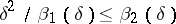 , there exists a
, there exists a 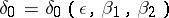 such that for
such that for 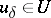 and
and 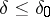 it follows from
it follows from 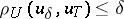 that
that 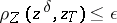 , where
, where 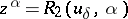 for all
for all 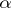 for which
for which  .
.
Methods for finding the regularization parameter depend on the additional information available on the problem. If the error of the right-hand side of the equation for 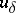 is known, say
is known, say 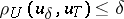 , then in accordance with the preceding it is natural to determine
, then in accordance with the preceding it is natural to determine 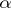 by the discrepancy, that is, from the relation
by the discrepancy, that is, from the relation 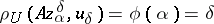 .
.
The function 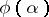 is monotone and semi-continuous for every
is monotone and semi-continuous for every 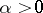 . If
. If 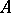 is a linear operator,
is a linear operator, 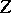 a Hilbert space and
a Hilbert space and 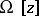 a strictly-convex functional (for example, quadratic), then the element
a strictly-convex functional (for example, quadratic), then the element 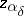 is unique and
is unique and 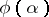 is a single-valued function. Under these conditions, for every positive number
is a single-valued function. Under these conditions, for every positive number 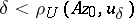 , where
, where 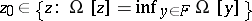 , there is an
, there is an 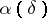 such that
such that 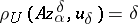 (see [TiArAr]).
(see [TiArAr]).
However, for a non-linear operator 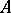 the equation
the equation 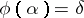 may have no solution (see [GoLeYa]).
may have no solution (see [GoLeYa]).
The regularization method is closely connected with the construction of splines (cf. Spline). For example, the problem of finding a function 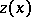 with piecewise-continuous second-order derivative on
with piecewise-continuous second-order derivative on 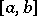 that minimizes the functional
that minimizes the functional 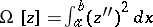 and takes given values
and takes given values 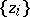 on a grid
on a grid 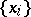 , is equivalent to the construction of a spline of the second degree.
, is equivalent to the construction of a spline of the second degree.
A regularizing operator can be constructed by spectral methods (see [TiArAr], [GoLeYa]), by means of the classical integral transforms in the case of equations of convolution type (see [Ar], [TiArAr]), by the method of quasi-mappings (see [LaLi]), or by the iteration method (see [Kr]). Necessary and sufficient conditions for the existence of a regularizing operator are known (see [Vi]).
Next, suppose that not only the right-hand side of (1) but also the operator 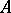 is given approximately, so that instead of the exact initial data
is given approximately, so that instead of the exact initial data 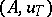 one has
one has 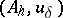 , where
, where
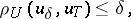 |
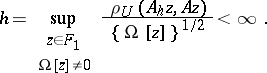 |
Under these conditions the procedure for obtaining an approximate solution is the same, only instead of 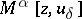 one has to consider the functional
one has to consider the functional
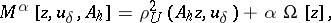 |
and the parameter 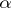 can be determined, for example, from the relation (see [TiArAr])
can be determined, for example, from the relation (see [TiArAr])
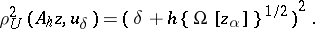 |
If (1) has an infinite set of solutions, one introduces the concept of a normal solution. Suppose that 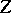 is a normed space. Then one can take, for example, a solution
is a normed space. Then one can take, for example, a solution  for which the deviation in norm from a given element
for which the deviation in norm from a given element 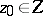 is minimal, that is,
is minimal, that is,
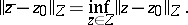 |
An approximation to a normal solution that is stable under small changes in the right-hand side of (1) can be found by the regularization method described above. The class of problems with infinitely many solutions includes degenerate systems of linear algebraic equations. So-called badly-conditioned systems of linear algebraic equations can be regarded as systems obtained from degenerate ones when the operator 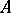 is replaced by its approximation
is replaced by its approximation 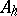 . As a normal solution of a corresponding degenerate system one can take a solution
. As a normal solution of a corresponding degenerate system one can take a solution  of minimal norm
of minimal norm 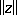 . In the smoothing functional one can take for
. In the smoothing functional one can take for 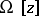 the functional
the functional 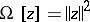 . Approximate solutions of badly-conditioned systems can also be found by the regularization method with
. Approximate solutions of badly-conditioned systems can also be found by the regularization method with 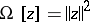 (see [TiArAr]).
(see [TiArAr]).
Similar methods can be used to solve a Fredholm integral equation of the second kind in the spectrum, that is, when the parameter 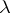 of the equation is equal to one of the eigen values of the kernel.
of the equation is equal to one of the eigen values of the kernel.
Instability problems in the minimization of functionals.
A number of problems important in practice leads to the minimization of functionals 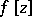 . One distinguishes two types of such problems. In the first class one has to find a minimal (or maximal) value of the functional. Many problems in the design of optimal systems or constructions fall in this class. For such problems it is irrelevant on what elements the required minimum is attained. Therefore, as approximate solutions of such problems one can take the values of the functional
. One distinguishes two types of such problems. In the first class one has to find a minimal (or maximal) value of the functional. Many problems in the design of optimal systems or constructions fall in this class. For such problems it is irrelevant on what elements the required minimum is attained. Therefore, as approximate solutions of such problems one can take the values of the functional 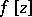 on any minimizing sequence
on any minimizing sequence 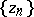 .
.
In the second type of problems one has to find elements  on which the minimum of
on which the minimum of 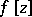 is attained. They are called problems of minimizing over the argument. E.g., the minimizing sequences may be divergent. In these problems one cannot take as approximate solutions the elements of minimizing sequences. Such problems are called unstable or ill-posed. These include, for example, problems of optimal control, in which the function to be optimized (the object function) depends only on the phase variables.
is attained. They are called problems of minimizing over the argument. E.g., the minimizing sequences may be divergent. In these problems one cannot take as approximate solutions the elements of minimizing sequences. Such problems are called unstable or ill-posed. These include, for example, problems of optimal control, in which the function to be optimized (the object function) depends only on the phase variables.
Suppose that 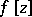 is a continuous functional on a metric space
is a continuous functional on a metric space 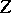 and that there is an element
and that there is an element 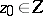 minimizing
minimizing 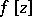 . A minimizing sequence
. A minimizing sequence 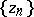 of
of 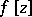 is called regularizing if there is a compact set
is called regularizing if there is a compact set 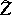 in
in 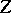 containing
containing 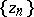 . If the minimization problem for
. If the minimization problem for 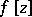 has a unique solution
has a unique solution 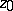 , then a regularizing minimizing sequence converges to
, then a regularizing minimizing sequence converges to 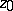 , and under these conditions it is sufficient to exhibit algorithms for the construction of regularizing minimizing sequences. This can be done by using stabilizing functionals
, and under these conditions it is sufficient to exhibit algorithms for the construction of regularizing minimizing sequences. This can be done by using stabilizing functionals 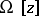 .
.
Let 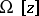 be a stabilizing functional defined on a set
be a stabilizing functional defined on a set 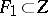 , let
, let 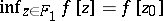 and let
and let 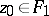 . Frequently, instead of
. Frequently, instead of 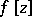 one takes its
one takes its 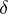 -approximation
-approximation 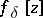 relative to
relative to 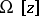 , that is, a functional such that for every
, that is, a functional such that for every 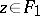 ,
,
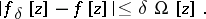 |
Then for any 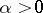 the problem of minimizing the functional
the problem of minimizing the functional
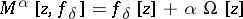 |
over the argument is stable.
Let 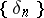 and
and 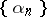 be null-sequences such that
be null-sequences such that 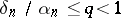 for every
for every  , and let
, and let 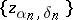 be a sequence of elements minimizing
be a sequence of elements minimizing 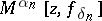 . This is a regularizing minimizing sequence for the functional
. This is a regularizing minimizing sequence for the functional 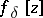 (see [TiArAr]), consequently, it converges as
(see [TiArAr]), consequently, it converges as 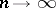 to an element
to an element 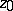 . As approximate solutions of the problems one can then take the elements
. As approximate solutions of the problems one can then take the elements 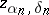 .
.
Similarly approximate solutions of ill-posed problems in optimal control can be constructed.
In applications ill-posed problems often occur where the initial data contain random errors. For the construction of approximate solutions to such classes both deterministic and probability approaches are possible (see [TiArAr], [LaVa]).
References
| [Ar] | V.Ya. Arsenin, "On a method for obtaining approximate solutions to convolution integral equations of the first kind" Proc. Steklov Inst. Math., 133 (1977) pp. 31–48 Trudy Mat. Inst. Steklov., 133 (1973) pp. 33–51 |
| [Ba] | A.B. Bakushinskii, "A general method for constructing regularizing algorithms for a linear ill-posed equation in Hilbert space" USSR Comp. Math. Math. Phys., 7 : 3 (1968) pp. 279–287 Zh. Vychisl. Mat. i Mat. Fiz., 7 : 3 (1967) pp. 672–677 |
| [GoLeYa] | A.V. Goncharskii, A.S. Leonov, A.G. Yagoda, "On the residual principle for solving nonlinear ill-posed problems" Soviet Math. Dokl., 15 (1974) pp. 166–168 Dokl. Akad. Nauk SSSR, 214 : 3 (1974) pp. 499–500 |
| [Iv] | V.K. Ivanov, "On ill-posed problems" Mat. Sb., 61 : 2 (1963) pp. 211–223 (In Russian) |
| [Iv2] | V.K. Ivanov, "On linear problems which are not well-posed" Soviet Math. Dokl., 3 (1962) pp. 981–983 Dokl. Akad. Nauk SSSR, 145 : 2 (1962) pp. 270–272 |
| [Kr] | A.V. Kryanev, "The solution of incorrectly posed problems by methods of successive approximations" Soviet Math. Dokl., 14 (1973) pp. 673–676 Dokl. Akad. Nauk SSSR, 210 : 1 pp. 20–22 |
| [LaLa] | M.M. [M.A. Lavrent'ev] Lavrentiev, "Some improperly posed problems of mathematical physics", Springer (1967) (Translated from Russian) |
| [LaLi] | R. Lattes, J.L. Lions, "Méthode de quasi-réversibilité et applications", Dunod (1967) |
| [LaVa] | M.M. Lavrent'ev, V.G. Vasil'ev, "The posing of certain improper problems of mathematical physics" Sib. Math. J., 7 : 3 (1966) pp. 450–463 Sibirsk. Mat. Zh., 7 : 3 (1966) pp. 559–576 |
| [Ti] | A.N. Tikhonov, "Solution of incorrectly formulated problems and the regularization method" Soviet Math. Dokl., 4 (1963) pp. 1035–1038 Dokl. Akad. Nauk SSSR, 151 : 3 (1963) pp. 501–504 |
| [Ti2] | A.N. Tikhonov, "Regularization of incorrectly posed problems" Soviet Math. Dokl., 4 (1963) pp. 1624–1627 Dokl. Akad. Nauk SSSR, 153 : 1 (1963) pp. 49–52 |
| [Ti3] | A.N. Tikhonov, "On stability of inverse problems" Dokl. Akad. Nauk SSSR, 39 : 5 (1943) pp. 176–179 (In Russian) |
| [Ti4] | A.N. Tikhonov, "On the stability of the functional optimization problem" USSR Comp. Math. Math. Phys., 6 : 4 (1966) pp. 28–33 Zh. Vychisl. Mat. i Mat. Fiz., 6 : 4 (1966) pp. 631–634 |
| [TiArAr] | A.N. Tikhonov, V.I. [V.I. Arsenin] Arsenine, "Solution of ill-posed problems", Winston (1977) (Translated from Russian) |
| [Vi] | V.A. Vinokurov, "On the regularization of discontinuous mappings" USSR Comp. Math. Math. Phys., 11 : 5 (1971) pp. 1–21 Zh. Vychisl. Mat. i Mat. Fiz., 11 : 5 (1971) pp. 1097–1112 |
Comments
The idea of conditional well-posedness was also found by B.L. Phillips [Ph]; the expression "Tikhonov well-posed" is not used in the West.
Other problems that lead to ill-posed problems in the sense described above are the Dirichlet problem for the wave equation, the non-characteristic Cauchy problem for the heat equation, the initial boundary value problem for the backward heat equation, inverse scattering problems ([CoKr]), identification of parameters (coefficients) in partial differential equations from over-specified data ([Ba2], [EnGr]), and computerized tomography ([Na2]).
If 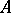 is a bounded linear operator between Hilbert spaces, then, as also mentioned above, regularization operators can be constructed via spectral theory: If
is a bounded linear operator between Hilbert spaces, then, as also mentioned above, regularization operators can be constructed via spectral theory: If 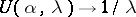 as
as  , then under mild assumptions,
, then under mild assumptions, 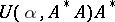 is a regularization operator (cf. [Gr]); for choices of the regularization parameter leading to optimal convergence rates for such methods see [EnGf]. For
is a regularization operator (cf. [Gr]); for choices of the regularization parameter leading to optimal convergence rates for such methods see [EnGf]. For 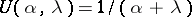 , the resulting method is called Tikhonov regularization: The regularized solution
, the resulting method is called Tikhonov regularization: The regularized solution 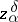 is defined via
is defined via 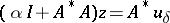 . A variant of this method in Hilbert scales has been developed in [Na] with parameter choice rules given in [Ne]. The parameter choice rule discussed in the article given by
. A variant of this method in Hilbert scales has been developed in [Na] with parameter choice rules given in [Ne]. The parameter choice rule discussed in the article given by 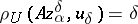 is called the discrepancy principle ([Mo]).
is called the discrepancy principle ([Mo]).
References
| [Ba2] | J. Baumeister, "Stable solution of inverse problems", Vieweg (1986) |
| [Ba3] | H.P. Baltes (ed.), Inverse source problems in optics, Springer (1978) |
| [Ba4] | H.P. Baltes (ed.), Inverse scattering problems in optics, Springer (1980) |
| [BaGi] | G. Backus, F. Gilbert, "The resolving power of gross earth data" Geophys. J. R. Astr. Soc., 16 (1968) |
| [BeBlSt] | J.V. Beck, B. Blackwell, C.R. StClair, "Inverse heat conduction: ill posed problems", Wiley (1985) |
| [BoJo] | W.M. Boerner, A.K. (eds.) Jordan, "Inverse methods in electromagnetics" IEEE Trans. Antennas Propag., 2 (1981) |
| [Ca] | J.R. Cann on, "The one-dimensional heat equation", Addison-Wesley (1984) |
| [CaSt] | A. Carasso, A.P. Stone, "Improperly posed boundary value problems", Pitman (1975) |
| [Co] | A.M. Cormak, "Representation of a function by its line integrals with some radiological applications" J. Appl. Phys., 34 (1963) |
| [Co2] | L. Colin, "Mathematics of profile inversion", Proc. Workshop Ames Res. Center, June 12–16, 1971, TM-X-62.150, NASA |
| [CoKr] | D.L. Colton, R. Kress, "Integral equation methods in scattering theory", Wiley (1983) |
| [EnGf] | H.W. Engl, H. Gfrerer, "A posteriori parameter choice for general regularization methods for solving linear ill-posed problems" Appl. Num. Math., 4 (1988) pp. 395–417 |
| [EnGr] | H.W. Engl (ed.) C.W. Groetsch (ed.), Inverse and ill-posed problems, Acad. Press (1987) |
| [Gr] | C.W. Groetsch, "The theory of Tikhonov regularization for Fredholm equations of the first kind", Pitman (1984) |
| [Gr2] | C.W. Groetsch, "The theory of Tikhonov regularization for Fredholm equations of the first kind", Pitman (1984) |
| [He] | G.T. Herman (ed.), Image reconstruction from projections, Springer (1979) |
| [HeNa] | G.T. Herman (ed.) F. Natterer (ed.), Mathematical aspects of computerized tomography, Proc. Oberwolfach, February 10–16, 1980, Springer (1981) |
| [Jo] | F. John, "Continuous dependence on data for solutions of partial differential equations with a prescribed bound" Comm. Pure Appl. Math., 13 (1960) pp. 551–585 |
| [Ka] | M. Kac, "Can one hear the shape of a drum?" Amer. Math. Monthly, 73 (1966) pp. 1–23 |
| [LaRoSh] | M.H. Lavrent'ev, V.G. Romanov, S.P. Shishalskii, "Ill-posed problems of mathematical physics and analysis", Amer. Math. Soc. (1986) (Translated from Russian) |
| [Mo] | V.A. Morozov, "Methods for solving incorrectly posed problems", Springer (1984) (Translated from Russian) |
| [Na] | F. Natterer, "Error bounds for Tikhonov regularization in Hilbert scales" Applic. Analysis, 18 (1984) pp. 29–37 |
| [Na2] | F. Natterer, "The mathematics of computerized tomography", Wiley (1986) |
| [Ne] | A. Neubauer, "An a-posteriori parameter choice for Tikhonov regularization in Hilbert scales leading to optimal convergence rates" SIAM J. Numer. Anal., 25 (1988) pp. 1313–1326 |
| [Pa] | L.E. Payne, "Improperly posed problems in partial differential equations", SIAM (1975) |
| [Ph] | B.L. Phillips, "A technique for the numerical solution of certain integral equations of the first kind" J. ACM, 9 (1962) pp. 84–97 |
Ill-posed problems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ill-posed_problems&oldid=25060