Difference between revisions of "System of parameters of a module over a local ring"
From Encyclopedia of Mathematics
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 30 formulas, 28 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $( A , \mathfrak m )$ be an $r$-dimensional Noetherian ring (cf. also the section "Dimension of an associative algebra" in [[Dimension|Dimension]]). Then there exists an $\mathfrak{m}$-primary ideal generated by $r$ elements (cf., e.g., [[#References|[a1]]], p. 98, [[#References|[a2]]], p. 27). If $x _ { 1 } , \dots , x _ { r }$ generate such an $\mathfrak{m}$-primary ideal, they are said to be a system of parameters of $A$. The terminology comes from the situation that $( A , \mathfrak m )$ is the local ring of functions at a (singular) point on an [[Algebraic variety|algebraic variety]]. The system of parameters $x _ { 1 } , \dots , x _ { r }$ is a regular system of parameters if $x _ { 1 } , \dots , x _ { r }$ generate $\mathfrak{m}$, and in that case $( A , \mathfrak m )$ is a regular local ring. | ||
| − | + | More generally, if $M$ is a finitely-generated $A$-module of dimension $s$, then there are $y _ { 1 } , \dots , y _ { s } \in \mathfrak { m }$ such that $M / ( y _ { 1 } , \ldots , y _ { s } ) M$ is of finite length; in that case $y _ { 1 } , \dots , y _ { s }$ is called a system of parameters of $M$. | |
| − | + | The ideal $( y _ { 1 } , \dots , y _ { s } )$ is called a parameter ideal. | |
| − | + | For a semi-local ring $A$ with maximal ideals $m _ { 1 } , \dots , m _ { r }$, an ideal $\frak a$ is called an ideal of definition if | |
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130630/s13063024.png"/></td> </tr></table> | ||
| + | |||
| + | for some natural number $k$. If $A$ is of dimension $d$, then any set of $d$ elements that generates an ideal of definition is a system of parameters of $A$, [[#References|[a3]]], Sect. 4.9. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> H. Matsumura, "Commutative ring theory" , Cambridge Univ. Press (1989)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Nagata, "Local rings" , Interscience (1962)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D.G. Nothcott, "Lessons on rings, modules, and multiplicities" , Cambridge Univ. Press (1968)</td></tr></table> |
Latest revision as of 17:45, 1 July 2020
Let $( A , \mathfrak m )$ be an $r$-dimensional Noetherian ring (cf. also the section "Dimension of an associative algebra" in Dimension). Then there exists an $\mathfrak{m}$-primary ideal generated by $r$ elements (cf., e.g., [a1], p. 98, [a2], p. 27). If $x _ { 1 } , \dots , x _ { r }$ generate such an $\mathfrak{m}$-primary ideal, they are said to be a system of parameters of $A$. The terminology comes from the situation that $( A , \mathfrak m )$ is the local ring of functions at a (singular) point on an algebraic variety. The system of parameters $x _ { 1 } , \dots , x _ { r }$ is a regular system of parameters if $x _ { 1 } , \dots , x _ { r }$ generate $\mathfrak{m}$, and in that case $( A , \mathfrak m )$ is a regular local ring.
More generally, if $M$ is a finitely-generated $A$-module of dimension $s$, then there are $y _ { 1 } , \dots , y _ { s } \in \mathfrak { m }$ such that $M / ( y _ { 1 } , \ldots , y _ { s } ) M$ is of finite length; in that case $y _ { 1 } , \dots , y _ { s }$ is called a system of parameters of $M$.
The ideal $( y _ { 1 } , \dots , y _ { s } )$ is called a parameter ideal.
For a semi-local ring $A$ with maximal ideals $m _ { 1 } , \dots , m _ { r }$, an ideal $\frak a$ is called an ideal of definition if
 |
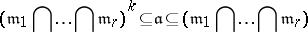for some natural number $k$. If $A$ is of dimension $d$, then any set of $d$ elements that generates an ideal of definition is a system of parameters of $A$, [a3], Sect. 4.9.
References
| [a1] | H. Matsumura, "Commutative ring theory" , Cambridge Univ. Press (1989) |
| [a2] | M. Nagata, "Local rings" , Interscience (1962) |
| [a3] | D.G. Nothcott, "Lessons on rings, modules, and multiplicities" , Cambridge Univ. Press (1968) |
How to Cite This Entry:
System of parameters of a module over a local ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_of_parameters_of_a_module_over_a_local_ring&oldid=18255
System of parameters of a module over a local ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_of_parameters_of_a_module_over_a_local_ring&oldid=18255
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article