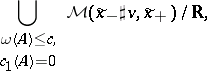|
|
| Line 1: |
Line 1: |
| | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | + | |
| | + | Out of 206 formulas, 199 were replaced by TEX code.--> |
| | + | |
| | + | {{TEX|semi-auto}}{{TEX|partial}} |
| | ''Flöer cohomology of symplectic manifolds'' | | ''Flöer cohomology of symplectic manifolds'' |
| | | | |
| Line 5: |
Line 13: |
| | Symplectic cohomology came out from the work of A. Flöer [[#References|[a3]]], [[#References|[a4]]] on the Arnol'd conjecture (concerning the minimal number of fixed points of a symplectic diffeomorphism), which can be reformulated as one of the above questions, and is mostly known in the literature as Flöer cohomology of symplectic manifolds. | | Symplectic cohomology came out from the work of A. Flöer [[#References|[a3]]], [[#References|[a4]]] on the Arnol'd conjecture (concerning the minimal number of fixed points of a symplectic diffeomorphism), which can be reformulated as one of the above questions, and is mostly known in the literature as Flöer cohomology of symplectic manifolds. |
| | | | |
| − | One can define symplectic cohomology for a symplectic manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203401.png" />, for a symplectic diffeomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203402.png" /> and for a pair of transversal Lagrangeans <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203403.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203404.png" />. Below, the first is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203405.png" />, the second by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203406.png" /> and the third by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203407.png" />. The Euler characteristic of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203408.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s1203409.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034010.png" /> are the standard [[Euler characteristic|Euler characteristic]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034011.png" />, the [[Lefschetz number|Lefschetz number]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034012.png" /> and the standard intersection number of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034014.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034015.png" />, respectively (cf. [[Intersection theory|Intersection theory]]). When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034016.png" /> is symplectically isotopic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034018.png" /> and when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034020.png" /> is the diagonal in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034021.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034022.png" /> is the graph of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034024.png" />. | + | One can define symplectic cohomology for a symplectic manifold $( M , \omega )$, for a symplectic diffeomorphism $\phi : ( M , \omega ) \rightarrow ( M , \omega )$ and for a pair of transversal Lagrangeans $( L _ { + } , L _ { - } )$ in $( M , \omega )$. Below, the first is denoted by $\operatorname{SH} ^ { * } ( M , \omega )$, the second by $\operatorname{SH} ^ { * } ( M , \omega , \phi )$ and the third by $\operatorname {SH} ^ { * } ( M , \omega , L _ { + } , L _ { - } )$. The Euler characteristic of $\operatorname{SH} ^ { * } ( M , \omega )$, $\operatorname{SH} ^ { * } ( M , \omega , \phi )$, and $\operatorname {SH} ^ { * } ( M , \omega , L _ { + } , L _ { - } )$ are the standard [[Euler characteristic|Euler characteristic]] of $M$, the [[Lefschetz number|Lefschetz number]] of $\phi$ and the standard intersection number of $L _ { + }$ and $L_{-}$ in $M$, respectively (cf. [[Intersection theory|Intersection theory]]). When $\phi$ is symplectically isotopic to $\operatorname{id}$, $\operatorname{SH} ^ { * } ( M , \omega ) = \operatorname{SH} ^ { * } ( M , \omega , \phi )$ and when $( N , \tilde{\omega} ) = ( M , \omega ) \times ( M , - \omega )$, $L _ { + }$ is the diagonal in $M \times M$ and $L_{-}$ is the graph of $\phi$, $\operatorname{SH} ^ { * } ( M , \omega , \phi ) = \operatorname{SH} ^ { * } ( N , \tilde { \omega } , L _ { + } , L - )$. |
| | | | |
| | One can define pairings | | One can define pairings |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034025.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname{SH} ^ { * } ( M , \omega , L _ { 1 } , L _ { 2 } ) \bigotimes \operatorname{SH} ^ { * } ( M , \omega , L _ { 2 } , L _ { 3 } ) \rightarrow \operatorname{SH} ^ { * } ( M , \omega , L _ { 1 } , L _ { 3 } ), \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034026.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname{SH} ^ { * } ( M , \omega , \phi _ { 1 } ) \bigotimes \operatorname{SH} ^ { * } ( M , \omega , \phi _ { 2 } ) \rightarrow \operatorname{SH} ^ { * } ( M , \omega , \phi _ { 2 } . \phi _ { 1 } ) \end{equation*} |
| | | | |
| | and | | and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034027.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname{SH} ^ { * } ( M , \omega ) \bigotimes \operatorname{SH} ^ { * } ( M , \omega ) \rightarrow \operatorname{SH} ^ { * } ( M , \omega ). \end{equation*} |
| | | | |
| − | The last pairing provides an associative product, known as the pair of pants product, hence a ring structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034028.png" />, cf. the section "Pair of pants product" below. | + | The last pairing provides an associative product, known as the pair of pants product, hence a ring structure on $\operatorname{SH} ^ { * } ( M , \omega )$, cf. the section "Pair of pants product" below. |
| | | | |
| − | As a group, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034029.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034030.png" /> and when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034031.png" /> is symplectically isotopic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034032.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034033.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034034.png" />, properly regraded. In the first case the "pair of pants" product is different from the cup product (cf. [[Cohomology|Cohomology]]) and the deviation of one from the other is measured by numerical invariants associated to the symplectic manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034035.png" />, the so-called Gromov–Witten invariants (cf. [[#References|[a1]]], Chap. 7). | + | As a group, $\operatorname{SH} ^ { * } ( M , \omega )$ is isomorphic to $H ^ { * } ( M ; \mathbf{Z} )$ and when $\phi$ is symplectically isotopic to $\operatorname{id}$, $SH ^ { * } ( M , \omega , L , \phi ( L ) )$ is isomorphic to $H ^ { * } ( L ; \mathbf{Z} )$, properly regraded. In the first case the "pair of pants" product is different from the cup product (cf. [[Cohomology|Cohomology]]) and the deviation of one from the other is measured by numerical invariants associated to the symplectic manifold $( M , \omega )$, the so-called Gromov–Witten invariants (cf. [[#References|[a1]]], Chap. 7). |
| | | | |
| − | With this ring structure the symplectic cohomology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034036.png" /> identifies to the quantum cohomology ring of the symplectic manifold (cf. [[#References|[a1]]], Chap. 10). | + | With this ring structure the symplectic cohomology $\operatorname{SH} ^ { * } ( M , \omega )$ identifies to the quantum cohomology ring of the symplectic manifold (cf. [[#References|[a1]]], Chap. 10). |
| | | | |
| − | The symplectic cohomologies mentioned above are not defined for all symplectic manifolds for technical reasons (cf. Definition c) below). The largest class of symplectic manifolds for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034037.png" /> is defined in [[#References|[a1]]] is the class of weakly symplectic manifolds. Recently, (cf. [[#References|[a6]]]) it was extended to all symplectic manifolds. | + | The symplectic cohomologies mentioned above are not defined for all symplectic manifolds for technical reasons (cf. Definition c) below). The largest class of symplectic manifolds for which $\operatorname{SH} ^ { * } ( M , \omega )$ is defined in [[#References|[a1]]] is the class of weakly symplectic manifolds. Recently, (cf. [[#References|[a6]]]) it was extended to all symplectic manifolds. |
| | | | |
| | ==Definitions.== | | ==Definitions.== |
| − | The definitions below are essentially due to Flöer (cf. [[#References|[a3]]], [[#References|[a4]]]) in the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034038.png" /> is monotonic and ameliorated and have been extended by others. This presentation closely follows [[#References|[a1]]]. | + | The definitions below are essentially due to Flöer (cf. [[#References|[a3]]], [[#References|[a4]]]) in the case $( M , \omega )$ is monotonic and ameliorated and have been extended by others. This presentation closely follows [[#References|[a1]]]. |
| | | | |
| − | For a [[Symplectic manifold|symplectic manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034039.png" /> one says that the [[Almost-complex structure|almost-complex structure]] (i.e., an automorphism of the [[Tangent bundle|tangent bundle]] whose square is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034040.png" />) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034041.png" /> tames <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034042.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034044.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034045.png" />. Such a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034046.png" /> defines a [[Riemannian metric|Riemannian metric]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034047.png" />. The space of all almost-complex structures which tame <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034048.png" /> is contractible (cf. also [[Contractible space|Contractible space]]), therefore the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034049.png" />s provide isomorphic complex [[Vector bundle|vector bundle]] structures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034050.png" />. Denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034051.png" /> the first [[Chern class|Chern class]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034052.png" />. | + | For a [[Symplectic manifold|symplectic manifold]] $( M , \omega )$ one says that the [[Almost-complex structure|almost-complex structure]] (i.e., an automorphism of the [[Tangent bundle|tangent bundle]] whose square is $- \operatorname{ Id }$) $J$ tames $\omega$ if $\omega ( J u , J v ) = \omega ( u , v )$, $\omega ( v , J v ) > 0$ for any $u , v \in T M$. Such a $J$ defines a [[Riemannian metric|Riemannian metric]] $g ( \omega , J )$. The space of all almost-complex structures which tame $\omega$ is contractible (cf. also [[Contractible space|Contractible space]]), therefore the $J$s provide isomorphic complex [[Vector bundle|vector bundle]] structures on $T M$. Denote by $c _ { 1 } \in H ^ { 2 } ( M ; \mathbf{Z} )$ the first [[Chern class|Chern class]] of $T M$. |
| | | | |
| − | An element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034053.png" /> is called spherical if it lies in the image of the Hurewicz isomorphism (cf. [[Homotopy group|Homotopy group]]). Denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034054.png" /> the smallest absolute value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034055.png" />. | + | An element $A \in H _ { 2 } ( M ; \mathbf{Z} )$ is called spherical if it lies in the image of the Hurewicz isomorphism (cf. [[Homotopy group|Homotopy group]]). Denote by $N$ the smallest absolute value $c_ { 1 } ( A )$. |
| | | | |
| − | The symplectic manifold is called monotonic if there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034056.png" /> so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034057.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034058.png" /> spherical, and weakly monotonic if it is either monotonic, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034059.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034060.png" /> spherical, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034061.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034062.png" />. | + | The symplectic manifold is called monotonic if there exists a $\lambda > 0$ so that $\omega ( A ) = \lambda c _ { 1 } ( A )$ for $A$ spherical, and weakly monotonic if it is either monotonic, or $c _ { 1 } ( A ) = 0$ for $A$ spherical, or $N \geq n - 2$, with $n = \operatorname { dim } M / 2$. |
| | | | |
| − | Given a symplectic manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034063.png" />, choose an almost-complex structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034064.png" /> which tames <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034065.png" /> and a (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034066.png" />-periodic) time-dependent potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034067.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034068.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034069.png" /> be the first Chern class of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034070.png" /> and denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034071.png" /> the space of (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034072.png" />-periodic) closed curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034073.png" /> which are homotopically trivial. Consider the covering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034074.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034075.png" /> whose points are equivalence classes of pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034076.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034077.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034078.png" />, with the equivalence relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034079.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034080.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034081.png" />. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034082.png" /> represents the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034083.png" />-cycle obtained by putting together the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034084.png" />-chains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034085.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034086.png" />. Define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034087.png" /> by the formula | + | Given a symplectic manifold $( M , \omega )$, choose an almost-complex structure $J$ which tames $\omega$ and a ($1$-periodic) time-dependent potential $H : S ^ { 1 } \times M \rightarrow \mathbf{R}$, $S ^ { 1 } = \mathbf{R} / \mathbf{Z}$. Let $c _ { 1 } \in H ^ { 2 } ( M ; \mathbf{Z} )$ be the first Chern class of $( T M , J )$ and denote by $P$ the space of ($1$-periodic) closed curves $x : S ^ { 1 } \rightarrow M$ which are homotopically trivial. Consider the covering $\tilde{P}$ of $P$ whose points are equivalence classes of pairs $\tilde{x} = ( x , u )$, $u : D ^ { 2 } \rightarrow M$, $u | _ { \partial D ^ { 2 } } = x$, with the equivalence relation $( x , u ) \equiv ( x ^ { \prime } , u ^ { \prime } )$ if and only if $x = x ^ { \prime }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034081.png"/>. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034082.png"/> represents the $2$-cycle obtained by putting together the $2$-chains $u ( D ^ { 2 } )$ and $- u ^ { \prime } ( D ^ { 2 } )$. Define $S _ { H } : \tilde{P} \rightarrow \mathbf{R}$ by the formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034088.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table>
| + | \begin{equation} \tag{a1} S _ { H } ( \tilde{x} ) = \int _ { D ^ { 2 } } u ^ { * } ( \omega ) + \int _ { 0 } ^ { 1 } H ( t , x ( t ) ) d t, \end{equation} |
| | | | |
| − | and observe that the critical points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034089.png" /> are exactly all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034090.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034091.png" /> a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034092.png" />-periodic trajectory of the Hamiltonian system associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034093.png" />. Denote the set of such critical points by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034094.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034095.png" /> is generic, all critical points are non-degenerate but of infinite Morse index. Fortunately, there exists a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034096.png" />, the Connely–Zehnder version of the Maslov index, cf. [[#References|[a2]]], so that for any two critical points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034097.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034098.png" />, the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s12034099.png" /> behaves as the difference of Morse indices in classical Morse theory. More precisely, one can prove that: | + | and observe that the critical points of $S _ { H }$ are exactly all $\tilde{x} = ( x , u )$ with $x$ a $1$-periodic trajectory of the Hamiltonian system associated to $H$. Denote the set of such critical points by $X$. When $H$ is generic, all critical points are non-degenerate but of infinite Morse index. Fortunately, there exists a $\alpha _ { H } : X \rightarrow \mathbf{Z}$, the Connely–Zehnder version of the Maslov index, cf. [[#References|[a2]]], so that for any two critical points $\tilde{x}$, $\tilde{y}$, the difference $\alpha _ { H } ( \tilde{y} ) - \alpha _ { H } ( \tilde { x } )$ behaves as the difference of Morse indices in classical Morse theory. More precisely, one can prove that: |
| | | | |
| − | a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340100.png" /> for any spherical class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340101.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340102.png" /> denotes the class represented by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340103.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340104.png" /> representing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340105.png" />. | + | a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340100.png"/> for any spherical class $A \in H _ { 2 } ( M ; \mathbf{Z} )$. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340102.png"/> denotes the class represented by $( x , u \sharp v )$ with $v : S ^ { 2 } \rightarrow M$ representing $A$. |
| | | | |
| − | b) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340106.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340107.png" /> are two critical points, then the mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340108.png" /> with the property that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340109.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340110.png" />, which satisfy the perturbed Cauchy–Riemann equations | + | b) If $\tilde{x}_ - = ( x_ - , u_ - )$ and $\tilde { x }_{ + }= ( x _ { + } , u _{+} )$ are two critical points, then the mappings $w : \mathbf{R} \times S ^ { 1 } \rightarrow M$ with the property that $\operatorname { lim } _ { s \rightarrow \pm \infty } w ( s , t ) = x _ { \pm } ( t )$ and $( x _ { + } , u _ { - } \sharp w ) \equiv \tilde{x} _ { + }$, which satisfy the perturbed Cauchy–Riemann equations |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340111.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table>
| + | \begin{equation} \tag{a2} \frac { \partial w } { \partial s } + J ( u ) \frac { \partial w } { \partial t } = \nabla H ( t , w ( s , t ) ), \end{equation} |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340112.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340113.png" />, are trajectories for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340114.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340115.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340116.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340117.png" /> is taken with respect to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340118.png" /> metric induced from the Riemannian metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340119.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340120.png" />. cf. [[#References|[a4]]]. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340121.png" /> is the obvious extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340122.png" /> provided by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340123.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340124.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340125.png" /> denotes the gradient on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340126.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340127.png" />. For generic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340128.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340129.png" />, the space of these mappings, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340130.png" />, is a smooth [[Manifold|manifold]] of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340131.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340132.png" /> acting freely on it (by translations on the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340133.png" />).
| + | $s \in \mathbf{T}$, $t \in S ^ { 1 }$, are trajectories for $\operatorname { grad } S _ { H }$ from $\tilde{x}_-$ to $\tilde { x } _ { + }$, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340117.png"/> is taken with respect to the $L_{2}$ metric induced from the Riemannian metric $g ( \omega , J )$ on $M$. cf. [[#References|[a4]]]. Here, $u_{ -} \sharp$ is the obvious extension of $x_{+}$ provided by $u_-$ and $w$ and $\nabla$ denotes the gradient on $M$ with respect to $g ( \omega , J )$. For generic $J$ and $H$, the space of these mappings, denoted by $\mathcal{M} ( \tilde { x } _ { - } , \tilde { x } _ { + } )$, is a smooth [[Manifold|manifold]] of dimension $\alpha _ { H } ( \tilde{x} _ { + } ) - \alpha _ { H } ( \tilde{x} _ { - } )$ with $\mathbf{R}$ acting freely on it (by translations on the parameter $s$). |
| | | | |
| − | c) For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340134.png" /> weakly monotonic, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340135.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340136.png" /> is compact; hence, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340137.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340138.png" /> generic, finite. Even more, in this case for any real number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340139.png" />, | + | c) For $( M , \omega )$ weakly monotonic, $\alpha _ { H } ( \tilde { x } _ { + } ) - \alpha _ { H } ( \tilde { x } _ { - } ) = 1$, ${\cal M} ( \tilde { x } _ { + } , \tilde { x } _ { - } ) / \bf R$ is compact; hence, when $J$ and $H$ generic, finite. Even more, in this case for any real number $c$, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340140.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340140.png"/></td> </tr></table> |
| | | | |
| − | with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340141.png" /> a spherical class in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340142.png" />, is compact, hence finite. The proof of c) relies on Gromov's theory of pseudo-holomorphic curves in symplectic manifolds, cf. [[#References|[a5]]] or [[#References|[a1]]] for more details. | + | with $A$ a spherical class in $H _ { 2 } ( M ; \mathbf{Z} )$, is compact, hence finite. The proof of c) relies on Gromov's theory of pseudo-holomorphic curves in symplectic manifolds, cf. [[#References|[a5]]] or [[#References|[a1]]] for more details. |
| | | | |
| − | As in Morse theory one can construct a cochain (or chain) complex generated by the points in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340143.png" />, graded with the help of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340144.png" /> and with coboundary given by the "algebraic" cardinality of the finite set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340145.png" />, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340146.png" />. Actually, c) permits one to "complete" this complex to a cochain complex of modules over the Novikov ring associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340147.png" /> (cf. [[#References|[a1]]], Chap. 9). The cohomology of this complex is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340148.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340149.png" /> and is the symplectic cohomology. | + | As in Morse theory one can construct a cochain (or chain) complex generated by the points in $X$, graded with the help of $\alpha _ { H }$ and with coboundary given by the "algebraic" cardinality of the finite set $\mathcal{M} ( \tilde { x } , \tilde { y } ) / \mathbf{R}$, when $\alpha _ { H } ( \tilde{y} ) - \alpha _ { H } ( \tilde{x} ) = 1$. Actually, c) permits one to "complete" this complex to a cochain complex of modules over the Novikov ring associated to $( M , \omega )$ (cf. [[#References|[a1]]], Chap. 9). The cohomology of this complex is independent of $J$ and $H$ and is the symplectic cohomology. |
| | | | |
| − | In the case of Lagrangean submanifolds <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340150.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340151.png" />, the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340152.png" /> consists of paths <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340153.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340154.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340155.png" />. There is no Hamiltonian, the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340156.png" /> is the symplectic action and (a2) become the Cauchy–Riemann equations. A function like <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340157.png" /> is not naturally defined, but the difference index of two critical points, an analogue of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340158.png" /> can be defined and is given by the classical Maslov index (cf. [[Fourier integral operator|Fourier integral operator]]). There is no natural <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340159.png" />-grading in this case but there is a natural <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340160.png" />-grading with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340161.png" /> as defined at the beginning. | + | In the case of Lagrangean submanifolds $L_{-}$ and $L _ { + }$, the space $P$ consists of paths $x: [ 0,1 ] \rightarrow M$ with $x ( 0 ) \in L _ { - }$ and $x ( 1 ) \in L _ { + }$. There is no Hamiltonian, the functional $S$ is the symplectic action and (a2) become the Cauchy–Riemann equations. A function like $\alpha _ { H }$ is not naturally defined, but the difference index of two critical points, an analogue of $\alpha _ { H } ( \tilde{y} ) - \alpha _ { H } ( \tilde { x } )$ can be defined and is given by the classical Maslov index (cf. [[Fourier integral operator|Fourier integral operator]]). There is no natural $\bf Z$-grading in this case but there is a natural $2 N$-grading with $N$ as defined at the beginning. |
| | | | |
| | ==Pair of pants product.== | | ==Pair of pants product.== |
| − | Consider a [[Riemann surface|Riemann surface]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340162.png" /> of genus zero with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340163.png" /> punctures. Choose a conformal parametrization of each of its three ends, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340164.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340165.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340166.png" /> disjoint, and put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340167.png" />. Choose an almost-complex structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340168.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340169.png" /> which tames <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340170.png" /> and a smooth mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340171.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340172.png" /> restricted to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340173.png" /> constant in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340174.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340175.png" />), and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340176.png" /> restricted to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340177.png" /> being zero. Put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340178.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340179.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340180.png" />. | + | Consider a [[Riemann surface|Riemann surface]] $\Sigma$ of genus zero with $3$ punctures. Choose a conformal parametrization of each of its three ends, $\varphi _ { 1 } , \varphi _ { 2 } : ( - \infty , 0 ) \times S ^ { 1 } \rightarrow \Sigma$ and $\varphi _ { 3 } : ( \infty , 0 ) \times S ^ { 1 } \rightarrow \Sigma$, with $U _ { i } = \varphi _ { i } ( ( \pm \infty , 0 ) \times S ^ { 1 } )$ disjoint, and put $\widetilde { \Sigma } = \Sigma \backslash \cup _ { i = 1,2,3 } U _ { i }$. Choose an almost-complex structure $J$ on $M$ which tames $\omega$ and a smooth mapping $H : \Sigma \times M \rightarrow \mathbf{R}$ with $H$ restricted to $U_i$ constant in $s$ ($s \in ( \pm \infty , \pm 1 )$), and $H$ restricted to $\widetilde{ \Sigma }$ being zero. Put $H _ { i } ( t , m ) = H ( \varphi _ { i } ( s , t ) , m )$, $t \in S ^ { 1 }$, $m \in M$. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340181.png" /> be a critical point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340182.png" />. Consider all mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340183.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340184.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340185.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340186.png" />, which restricted to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340187.png" /> satisfy the perturbed Cauchy–Riemann equations (a2) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340188.png" /> and when restricted to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340189.png" /> are pseudo-holomorphic curves. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340190.png" /> denotes the mapping obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340191.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340192.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340193.png" /> in the obvious way. | + | Let $\tilde { x } _ { i } = ( x _ { i } , u _ { i } )$ be a critical point of $S _ { H _ { i } }$. Consider all mappings $\sigma : \Sigma \rightarrow M$ with $\operatorname { lim } _ { s \rightarrow \pm \infty } ( \sigma \cdot \varphi _ { i } ( s , t ) ) = x _ { i } ( t )$, $i = 1,2,3$, and $( x _ { 3 } , u _ { 1 } \cup u _ { 2 } \cup \sigma ) \equiv ( x _ { 3 } , u _ { 3 } )$, which restricted to $U_i$ satisfy the perturbed Cauchy–Riemann equations (a2) for $H _ { i }$ and when restricted to $\widetilde{ \Sigma }$ are pseudo-holomorphic curves. Here, $u _ { 1 } \cup u _ { 2 } \cup \sigma : D ^ { 2 } \rightarrow M$ denotes the mapping obtained from $u_1$, $u_2$ and $w$ in the obvious way. |
| | | | |
| − | The theory of pseudo-holomorphic curves implies that when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340194.png" /> is weakly monotonic and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340195.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340196.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340197.png" /> are generic, the space of these mappings is a smooth manifold of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340198.png" />, while if this dimension is zero, this space is compact hence finite. Using the "algebraic" cardinality of these sets, one can define a pairing of the cochain complexes associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340199.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340200.png" /> into the cochain complex associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340201.png" /> (cf. [[#References|[a1]]], Chap. 10). Since the cohomology of these complexes is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340202.png" />, this pairing induces a pairing of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340203.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340204.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120340/s120340205.png" />, which turns out to be an associative product and is called the pair of pants product. | + | The theory of pseudo-holomorphic curves implies that when $( M , \omega )$ is weakly monotonic and $H _ { i }$, $i = 1,2$, $J$ are generic, the space of these mappings is a smooth manifold of dimension $\alpha _ { H _ { 3 } } - \alpha _ { H _ { 2 } } - \alpha _ { H _ { 1 } }$, while if this dimension is zero, this space is compact hence finite. Using the "algebraic" cardinality of these sets, one can define a pairing of the cochain complexes associated to $( H _ { 1 } , J )$ and $( H _ { 1 } , J )$ into the cochain complex associated to $( H _ { 3 } , J )$ (cf. [[#References|[a1]]], Chap. 10). Since the cohomology of these complexes is independent of $H _ { i }$, this pairing induces a pairing of $\operatorname{SH} ^ { * } ( M , \omega )$ and $\operatorname{SH} ^ { * } ( M , \omega )$ into $\operatorname{SH} ^ { * } ( M , \omega )$, which turns out to be an associative product and is called the pair of pants product. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. McDuff, D. Salamon, "J-holomorphic curves and quantum cohomology" , ''Univ. Lecture Ser.'' , '''6''' , Amer. Math. Soc. (1995)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D. Salamon, E. Zehnder, "Morse theory for periodic solutions of Hamiltonian systems and Maslov index" ''Commun. Pure Appl. Math.'' , '''45''' (1992) pp. 1303–1360</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Flöer, "Symplectic fixed points and holomorphic spheres" ''Comm. Math. Phys.'' , '''120''' (1989)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A. Flöer, "Morse theory for lagrangean intersections" ''J. Diff. Geom.'' , '''28''' (1988) pp. 513–547</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Gromov, "Pseudoholomorphic curves in symplectic manifolds" ''Invent. Math.'' , '''82''' (1985) pp. 307–347</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G. Liu, G. Tian, "Flöer homology and Arnold conjecture" ''J. Diff. Geom.'' , '''49''' (1998) pp. 1–74</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> D. McDuff, D. Salamon, "J-holomorphic curves and quantum cohomology" , ''Univ. Lecture Ser.'' , '''6''' , Amer. Math. Soc. (1995)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> D. Salamon, E. Zehnder, "Morse theory for periodic solutions of Hamiltonian systems and Maslov index" ''Commun. Pure Appl. Math.'' , '''45''' (1992) pp. 1303–1360</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A. Flöer, "Symplectic fixed points and holomorphic spheres" ''Comm. Math. Phys.'' , '''120''' (1989)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A. Flöer, "Morse theory for lagrangean intersections" ''J. Diff. Geom.'' , '''28''' (1988) pp. 513–547</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Gromov, "Pseudoholomorphic curves in symplectic manifolds" ''Invent. Math.'' , '''82''' (1985) pp. 307–347</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> G. Liu, G. Tian, "Flöer homology and Arnold conjecture" ''J. Diff. Geom.'' , '''49''' (1998) pp. 1–74</td></tr></table> |
Flöer cohomology of symplectic manifolds
While standard cohomology is very useful to answer questions about the zeros of vector fields, fixed points of diffeomorphisms, and the points of intersection of a pair of submanifolds of complementary dimension, symplectic cohomology is supposed to refine such answers in the case of symplectic manifolds, Hamiltonian vector fields, symplectic diffeomorphisms and Lagrangean submanifolds.
Symplectic cohomology came out from the work of A. Flöer [a3], [a4] on the Arnol'd conjecture (concerning the minimal number of fixed points of a symplectic diffeomorphism), which can be reformulated as one of the above questions, and is mostly known in the literature as Flöer cohomology of symplectic manifolds.
One can define symplectic cohomology for a symplectic manifold $( M , \omega )$, for a symplectic diffeomorphism $\phi : ( M , \omega ) \rightarrow ( M , \omega )$ and for a pair of transversal Lagrangeans $( L _ { + } , L _ { - } )$ in $( M , \omega )$. Below, the first is denoted by $\operatorname{SH} ^ { * } ( M , \omega )$, the second by $\operatorname{SH} ^ { * } ( M , \omega , \phi )$ and the third by $\operatorname {SH} ^ { * } ( M , \omega , L _ { + } , L _ { - } )$. The Euler characteristic of $\operatorname{SH} ^ { * } ( M , \omega )$, $\operatorname{SH} ^ { * } ( M , \omega , \phi )$, and $\operatorname {SH} ^ { * } ( M , \omega , L _ { + } , L _ { - } )$ are the standard Euler characteristic of $M$, the Lefschetz number of $\phi$ and the standard intersection number of $L _ { + }$ and $L_{-}$ in $M$, respectively (cf. Intersection theory). When $\phi$ is symplectically isotopic to $\operatorname{id}$, $\operatorname{SH} ^ { * } ( M , \omega ) = \operatorname{SH} ^ { * } ( M , \omega , \phi )$ and when $( N , \tilde{\omega} ) = ( M , \omega ) \times ( M , - \omega )$, $L _ { + }$ is the diagonal in $M \times M$ and $L_{-}$ is the graph of $\phi$, $\operatorname{SH} ^ { * } ( M , \omega , \phi ) = \operatorname{SH} ^ { * } ( N , \tilde { \omega } , L _ { + } , L - )$.
One can define pairings
\begin{equation*} \operatorname{SH} ^ { * } ( M , \omega , L _ { 1 } , L _ { 2 } ) \bigotimes \operatorname{SH} ^ { * } ( M , \omega , L _ { 2 } , L _ { 3 } ) \rightarrow \operatorname{SH} ^ { * } ( M , \omega , L _ { 1 } , L _ { 3 } ), \end{equation*}
\begin{equation*} \operatorname{SH} ^ { * } ( M , \omega , \phi _ { 1 } ) \bigotimes \operatorname{SH} ^ { * } ( M , \omega , \phi _ { 2 } ) \rightarrow \operatorname{SH} ^ { * } ( M , \omega , \phi _ { 2 } . \phi _ { 1 } ) \end{equation*}
and
\begin{equation*} \operatorname{SH} ^ { * } ( M , \omega ) \bigotimes \operatorname{SH} ^ { * } ( M , \omega ) \rightarrow \operatorname{SH} ^ { * } ( M , \omega ). \end{equation*}
The last pairing provides an associative product, known as the pair of pants product, hence a ring structure on $\operatorname{SH} ^ { * } ( M , \omega )$, cf. the section "Pair of pants product" below.
As a group, $\operatorname{SH} ^ { * } ( M , \omega )$ is isomorphic to $H ^ { * } ( M ; \mathbf{Z} )$ and when $\phi$ is symplectically isotopic to $\operatorname{id}$, $SH ^ { * } ( M , \omega , L , \phi ( L ) )$ is isomorphic to $H ^ { * } ( L ; \mathbf{Z} )$, properly regraded. In the first case the "pair of pants" product is different from the cup product (cf. Cohomology) and the deviation of one from the other is measured by numerical invariants associated to the symplectic manifold $( M , \omega )$, the so-called Gromov–Witten invariants (cf. [a1], Chap. 7).
With this ring structure the symplectic cohomology $\operatorname{SH} ^ { * } ( M , \omega )$ identifies to the quantum cohomology ring of the symplectic manifold (cf. [a1], Chap. 10).
The symplectic cohomologies mentioned above are not defined for all symplectic manifolds for technical reasons (cf. Definition c) below). The largest class of symplectic manifolds for which $\operatorname{SH} ^ { * } ( M , \omega )$ is defined in [a1] is the class of weakly symplectic manifolds. Recently, (cf. [a6]) it was extended to all symplectic manifolds.
Definitions.
The definitions below are essentially due to Flöer (cf. [a3], [a4]) in the case $( M , \omega )$ is monotonic and ameliorated and have been extended by others. This presentation closely follows [a1].
For a symplectic manifold $( M , \omega )$ one says that the almost-complex structure (i.e., an automorphism of the tangent bundle whose square is $- \operatorname{ Id }$) $J$ tames $\omega$ if $\omega ( J u , J v ) = \omega ( u , v )$, $\omega ( v , J v ) > 0$ for any $u , v \in T M$. Such a $J$ defines a Riemannian metric $g ( \omega , J )$. The space of all almost-complex structures which tame $\omega$ is contractible (cf. also Contractible space), therefore the $J$s provide isomorphic complex vector bundle structures on $T M$. Denote by $c _ { 1 } \in H ^ { 2 } ( M ; \mathbf{Z} )$ the first Chern class of $T M$.
An element $A \in H _ { 2 } ( M ; \mathbf{Z} )$ is called spherical if it lies in the image of the Hurewicz isomorphism (cf. Homotopy group). Denote by $N$ the smallest absolute value $c_ { 1 } ( A )$.
The symplectic manifold is called monotonic if there exists a $\lambda > 0$ so that $\omega ( A ) = \lambda c _ { 1 } ( A )$ for $A$ spherical, and weakly monotonic if it is either monotonic, or $c _ { 1 } ( A ) = 0$ for $A$ spherical, or $N \geq n - 2$, with $n = \operatorname { dim } M / 2$.
Given a symplectic manifold $( M , \omega )$, choose an almost-complex structure $J$ which tames $\omega$ and a ($1$-periodic) time-dependent potential $H : S ^ { 1 } \times M \rightarrow \mathbf{R}$, $S ^ { 1 } = \mathbf{R} / \mathbf{Z}$. Let $c _ { 1 } \in H ^ { 2 } ( M ; \mathbf{Z} )$ be the first Chern class of $( T M , J )$ and denote by $P$ the space of ($1$-periodic) closed curves $x : S ^ { 1 } \rightarrow M$ which are homotopically trivial. Consider the covering $\tilde{P}$ of $P$ whose points are equivalence classes of pairs $\tilde{x} = ( x , u )$, $u : D ^ { 2 } \rightarrow M$, $u | _ { \partial D ^ { 2 } } = x$, with the equivalence relation $( x , u ) \equiv ( x ^ { \prime } , u ^ { \prime } )$ if and only if $x = x ^ { \prime }$ and 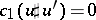 . Here,
. Here, 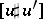 represents the $2$-cycle obtained by putting together the $2$-chains $u ( D ^ { 2 } )$ and $- u ^ { \prime } ( D ^ { 2 } )$. Define $S _ { H } : \tilde{P} \rightarrow \mathbf{R}$ by the formula
represents the $2$-cycle obtained by putting together the $2$-chains $u ( D ^ { 2 } )$ and $- u ^ { \prime } ( D ^ { 2 } )$. Define $S _ { H } : \tilde{P} \rightarrow \mathbf{R}$ by the formula
\begin{equation} \tag{a1} S _ { H } ( \tilde{x} ) = \int _ { D ^ { 2 } } u ^ { * } ( \omega ) + \int _ { 0 } ^ { 1 } H ( t , x ( t ) ) d t, \end{equation}
and observe that the critical points of $S _ { H }$ are exactly all $\tilde{x} = ( x , u )$ with $x$ a $1$-periodic trajectory of the Hamiltonian system associated to $H$. Denote the set of such critical points by $X$. When $H$ is generic, all critical points are non-degenerate but of infinite Morse index. Fortunately, there exists a $\alpha _ { H } : X \rightarrow \mathbf{Z}$, the Connely–Zehnder version of the Maslov index, cf. [a2], so that for any two critical points $\tilde{x}$, $\tilde{y}$, the difference $\alpha _ { H } ( \tilde{y} ) - \alpha _ { H } ( \tilde { x } )$ behaves as the difference of Morse indices in classical Morse theory. More precisely, one can prove that:
a) 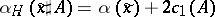 for any spherical class $A \in H _ { 2 } ( M ; \mathbf{Z} )$. Here
for any spherical class $A \in H _ { 2 } ( M ; \mathbf{Z} )$. Here 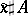 denotes the class represented by $( x , u \sharp v )$ with $v : S ^ { 2 } \rightarrow M$ representing $A$.
denotes the class represented by $( x , u \sharp v )$ with $v : S ^ { 2 } \rightarrow M$ representing $A$.
b) If $\tilde{x}_ - = ( x_ - , u_ - )$ and $\tilde { x }_{ + }= ( x _ { + } , u _{+} )$ are two critical points, then the mappings $w : \mathbf{R} \times S ^ { 1 } \rightarrow M$ with the property that $\operatorname { lim } _ { s \rightarrow \pm \infty } w ( s , t ) = x _ { \pm } ( t )$ and $( x _ { + } , u _ { - } \sharp w ) \equiv \tilde{x} _ { + }$, which satisfy the perturbed Cauchy–Riemann equations
\begin{equation} \tag{a2} \frac { \partial w } { \partial s } + J ( u ) \frac { \partial w } { \partial t } = \nabla H ( t , w ( s , t ) ), \end{equation}
$s \in \mathbf{T}$, $t \in S ^ { 1 }$, are trajectories for $\operatorname { grad } S _ { H }$ from $\tilde{x}_-$ to $\tilde { x } _ { + }$, where 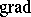 is taken with respect to the $L_{2}$ metric induced from the Riemannian metric $g ( \omega , J )$ on $M$. cf. [a4]. Here, $u_{ -} \sharp$ is the obvious extension of $x_{+}$ provided by $u_-$ and $w$ and $\nabla$ denotes the gradient on $M$ with respect to $g ( \omega , J )$. For generic $J$ and $H$, the space of these mappings, denoted by $\mathcal{M} ( \tilde { x } _ { - } , \tilde { x } _ { + } )$, is a smooth manifold of dimension $\alpha _ { H } ( \tilde{x} _ { + } ) - \alpha _ { H } ( \tilde{x} _ { - } )$ with $\mathbf{R}$ acting freely on it (by translations on the parameter $s$).
is taken with respect to the $L_{2}$ metric induced from the Riemannian metric $g ( \omega , J )$ on $M$. cf. [a4]. Here, $u_{ -} \sharp$ is the obvious extension of $x_{+}$ provided by $u_-$ and $w$ and $\nabla$ denotes the gradient on $M$ with respect to $g ( \omega , J )$. For generic $J$ and $H$, the space of these mappings, denoted by $\mathcal{M} ( \tilde { x } _ { - } , \tilde { x } _ { + } )$, is a smooth manifold of dimension $\alpha _ { H } ( \tilde{x} _ { + } ) - \alpha _ { H } ( \tilde{x} _ { - } )$ with $\mathbf{R}$ acting freely on it (by translations on the parameter $s$).
c) For $( M , \omega )$ weakly monotonic, $\alpha _ { H } ( \tilde { x } _ { + } ) - \alpha _ { H } ( \tilde { x } _ { - } ) = 1$, ${\cal M} ( \tilde { x } _ { + } , \tilde { x } _ { - } ) / \bf R$ is compact; hence, when $J$ and $H$ generic, finite. Even more, in this case for any real number $c$,
with $A$ a spherical class in $H _ { 2 } ( M ; \mathbf{Z} )$, is compact, hence finite. The proof of c) relies on Gromov's theory of pseudo-holomorphic curves in symplectic manifolds, cf. [a5] or [a1] for more details.
As in Morse theory one can construct a cochain (or chain) complex generated by the points in $X$, graded with the help of $\alpha _ { H }$ and with coboundary given by the "algebraic" cardinality of the finite set $\mathcal{M} ( \tilde { x } , \tilde { y } ) / \mathbf{R}$, when $\alpha _ { H } ( \tilde{y} ) - \alpha _ { H } ( \tilde{x} ) = 1$. Actually, c) permits one to "complete" this complex to a cochain complex of modules over the Novikov ring associated to $( M , \omega )$ (cf. [a1], Chap. 9). The cohomology of this complex is independent of $J$ and $H$ and is the symplectic cohomology.
In the case of Lagrangean submanifolds $L_{-}$ and $L _ { + }$, the space $P$ consists of paths $x: [ 0,1 ] \rightarrow M$ with $x ( 0 ) \in L _ { - }$ and $x ( 1 ) \in L _ { + }$. There is no Hamiltonian, the functional $S$ is the symplectic action and (a2) become the Cauchy–Riemann equations. A function like $\alpha _ { H }$ is not naturally defined, but the difference index of two critical points, an analogue of $\alpha _ { H } ( \tilde{y} ) - \alpha _ { H } ( \tilde { x } )$ can be defined and is given by the classical Maslov index (cf. Fourier integral operator). There is no natural $\bf Z$-grading in this case but there is a natural $2 N$-grading with $N$ as defined at the beginning.
Pair of pants product.
Consider a Riemann surface $\Sigma$ of genus zero with $3$ punctures. Choose a conformal parametrization of each of its three ends, $\varphi _ { 1 } , \varphi _ { 2 } : ( - \infty , 0 ) \times S ^ { 1 } \rightarrow \Sigma$ and $\varphi _ { 3 } : ( \infty , 0 ) \times S ^ { 1 } \rightarrow \Sigma$, with $U _ { i } = \varphi _ { i } ( ( \pm \infty , 0 ) \times S ^ { 1 } )$ disjoint, and put $\widetilde { \Sigma } = \Sigma \backslash \cup _ { i = 1,2,3 } U _ { i }$. Choose an almost-complex structure $J$ on $M$ which tames $\omega$ and a smooth mapping $H : \Sigma \times M \rightarrow \mathbf{R}$ with $H$ restricted to $U_i$ constant in $s$ ($s \in ( \pm \infty , \pm 1 )$), and $H$ restricted to $\widetilde{ \Sigma }$ being zero. Put $H _ { i } ( t , m ) = H ( \varphi _ { i } ( s , t ) , m )$, $t \in S ^ { 1 }$, $m \in M$.
Let $\tilde { x } _ { i } = ( x _ { i } , u _ { i } )$ be a critical point of $S _ { H _ { i } }$. Consider all mappings $\sigma : \Sigma \rightarrow M$ with $\operatorname { lim } _ { s \rightarrow \pm \infty } ( \sigma \cdot \varphi _ { i } ( s , t ) ) = x _ { i } ( t )$, $i = 1,2,3$, and $( x _ { 3 } , u _ { 1 } \cup u _ { 2 } \cup \sigma ) \equiv ( x _ { 3 } , u _ { 3 } )$, which restricted to $U_i$ satisfy the perturbed Cauchy–Riemann equations (a2) for $H _ { i }$ and when restricted to $\widetilde{ \Sigma }$ are pseudo-holomorphic curves. Here, $u _ { 1 } \cup u _ { 2 } \cup \sigma : D ^ { 2 } \rightarrow M$ denotes the mapping obtained from $u_1$, $u_2$ and $w$ in the obvious way.
The theory of pseudo-holomorphic curves implies that when $( M , \omega )$ is weakly monotonic and $H _ { i }$, $i = 1,2$, $J$ are generic, the space of these mappings is a smooth manifold of dimension $\alpha _ { H _ { 3 } } - \alpha _ { H _ { 2 } } - \alpha _ { H _ { 1 } }$, while if this dimension is zero, this space is compact hence finite. Using the "algebraic" cardinality of these sets, one can define a pairing of the cochain complexes associated to $( H _ { 1 } , J )$ and $( H _ { 1 } , J )$ into the cochain complex associated to $( H _ { 3 } , J )$ (cf. [a1], Chap. 10). Since the cohomology of these complexes is independent of $H _ { i }$, this pairing induces a pairing of $\operatorname{SH} ^ { * } ( M , \omega )$ and $\operatorname{SH} ^ { * } ( M , \omega )$ into $\operatorname{SH} ^ { * } ( M , \omega )$, which turns out to be an associative product and is called the pair of pants product.
References
| [a1] | D. McDuff, D. Salamon, "J-holomorphic curves and quantum cohomology" , Univ. Lecture Ser. , 6 , Amer. Math. Soc. (1995) |
| [a2] | D. Salamon, E. Zehnder, "Morse theory for periodic solutions of Hamiltonian systems and Maslov index" Commun. Pure Appl. Math. , 45 (1992) pp. 1303–1360 |
| [a3] | A. Flöer, "Symplectic fixed points and holomorphic spheres" Comm. Math. Phys. , 120 (1989) |
| [a4] | A. Flöer, "Morse theory for lagrangean intersections" J. Diff. Geom. , 28 (1988) pp. 513–547 |
| [a5] | M. Gromov, "Pseudoholomorphic curves in symplectic manifolds" Invent. Math. , 82 (1985) pp. 307–347 |
| [a6] | G. Liu, G. Tian, "Flöer homology and Arnold conjecture" J. Diff. Geom. , 49 (1998) pp. 1–74 |
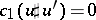 . Here,
. Here, 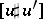 represents the $2$-cycle obtained by putting together the $2$-chains $u ( D ^ { 2 } )$ and $- u ^ { \prime } ( D ^ { 2 } )$. Define $S _ { H } : \tilde{P} \rightarrow \mathbf{R}$ by the formula
represents the $2$-cycle obtained by putting together the $2$-chains $u ( D ^ { 2 } )$ and $- u ^ { \prime } ( D ^ { 2 } )$. Define $S _ { H } : \tilde{P} \rightarrow \mathbf{R}$ by the formula
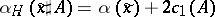 for any spherical class $A \in H _ { 2 } ( M ; \mathbf{Z} )$. Here
for any spherical class $A \in H _ { 2 } ( M ; \mathbf{Z} )$. Here 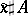 denotes the class represented by $( x , u \sharp v )$ with $v : S ^ { 2 } \rightarrow M$ representing $A$.
denotes the class represented by $( x , u \sharp v )$ with $v : S ^ { 2 } \rightarrow M$ representing $A$.
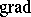 is taken with respect to the $L_{2}$ metric induced from the Riemannian metric $g ( \omega , J )$ on $M$. cf. [a4]. Here, $u_{ -} \sharp$ is the obvious extension of $x_{+}$ provided by $u_-$ and $w$ and $\nabla$ denotes the gradient on $M$ with respect to $g ( \omega , J )$. For generic $J$ and $H$, the space of these mappings, denoted by $\mathcal{M} ( \tilde { x } _ { - } , \tilde { x } _ { + } )$, is a smooth manifold of dimension $\alpha _ { H } ( \tilde{x} _ { + } ) - \alpha _ { H } ( \tilde{x} _ { - } )$ with $\mathbf{R}$ acting freely on it (by translations on the parameter $s$).
is taken with respect to the $L_{2}$ metric induced from the Riemannian metric $g ( \omega , J )$ on $M$. cf. [a4]. Here, $u_{ -} \sharp$ is the obvious extension of $x_{+}$ provided by $u_-$ and $w$ and $\nabla$ denotes the gradient on $M$ with respect to $g ( \omega , J )$. For generic $J$ and $H$, the space of these mappings, denoted by $\mathcal{M} ( \tilde { x } _ { - } , \tilde { x } _ { + } )$, is a smooth manifold of dimension $\alpha _ { H } ( \tilde{x} _ { + } ) - \alpha _ { H } ( \tilde{x} _ { - } )$ with $\mathbf{R}$ acting freely on it (by translations on the parameter $s$).