Symmetric group
The group of all permutations (self-bijections) of a set  with the operation of composition (see Permutation group). The symmetric group on a set
with the operation of composition (see Permutation group). The symmetric group on a set  is denoted by
is denoted by  . For equipotent
. For equipotent  and
and  the groups
the groups  and
and  are isomorphic. The symmetric group of a finite set
are isomorphic. The symmetric group of a finite set  is denoted by
is denoted by  . Every abstract group is isomorphic to a subgroup of the symmetric group
. Every abstract group is isomorphic to a subgroup of the symmetric group  of some set
of some set 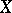 (Cayley's theorem).
(Cayley's theorem).
Let  be a finite set. Every permutation
be a finite set. Every permutation 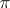 on
on 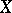 can be uniquely described as a product of disjoint cycles (the (disjoint) cycle decomposition of a permutation); the sequence of integers
can be uniquely described as a product of disjoint cycles (the (disjoint) cycle decomposition of a permutation); the sequence of integers
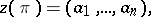 |
where 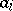 is the number of cycles of length
is the number of cycles of length  of
of 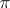 , is called the cycle type (or cycle index) of
, is called the cycle type (or cycle index) of 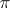 . Two permutations
. Two permutations 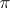 and
and 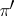 are conjugate in
are conjugate in 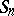 if and only if they have the same cycle type. Permutations with cycle type
if and only if they have the same cycle type. Permutations with cycle type
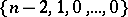 |
are called transpositions; they form a system of generators for 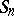 . The set of transpositions
. The set of transpositions 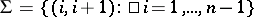 is a minimal set of generators for
is a minimal set of generators for 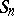 . In general, a set
. In general, a set 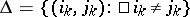 generates
generates 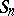 if the graph with
if the graph with  as set of vertices and the pairs
as set of vertices and the pairs 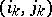 as edges is a tree [2]. The number of such generating sets is
as edges is a tree [2]. The number of such generating sets is 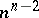 .
.
The alternating group 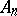 is a normal subgroup of
is a normal subgroup of 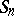 . If
. If 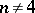 ,
, 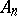 is the unique non-trivial proper normal subgroup, and
is the unique non-trivial proper normal subgroup, and 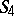 contains only one other non-trivial normal subgroup — the Klein four-group:
contains only one other non-trivial normal subgroup — the Klein four-group: 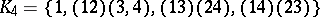 . For
. For 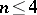 the group
the group  is solvable, but for
is solvable, but for 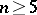 it is not solvable and
it is not solvable and 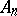 is a simple non-Abelian group. Hölder's theorem: For
is a simple non-Abelian group. Hölder's theorem: For  , the group
, the group  is complete (see Complete group). The group
is complete (see Complete group). The group  is commutative, and
is commutative, and 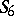 has an outer automorphism of order 2.
has an outer automorphism of order 2.
All maximal intransitive and imprimitive subgroups in 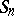 are known. For each partition
are known. For each partition 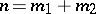 ,
, 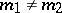 , the only maximal intransitive subgroups in
, the only maximal intransitive subgroups in  are the subgroups
are the subgroups  . The only transitive imprimitive maximal subgroups in
. The only transitive imprimitive maximal subgroups in  are the wreath products (cf. Wreath product) of
are the wreath products (cf. Wreath product) of 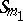 with
with  (for every decomposition
(for every decomposition  ). The primitive maximal subgroups in
). The primitive maximal subgroups in 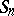 have not yet been described (1992), but certain infinite series of them are known. For example,
have not yet been described (1992), but certain infinite series of them are known. For example,  acts naturally on the set
acts naturally on the set 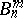 of all subsets of
of all subsets of 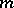 elements of
elements of  ; for
; for 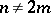 this determines a primitive group of permutations of
this determines a primitive group of permutations of  . It is maximal in
. It is maximal in 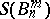 if
if 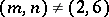 ,
,  ,
, 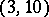 ,
,  ,
, 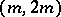 ,
, 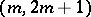 (see [1]). Another series is obtained by considering the group
(see [1]). Another series is obtained by considering the group 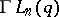 of semi-linear transformations of the
of semi-linear transformations of the  -dimensional vector space over the finite field of
-dimensional vector space over the finite field of  elements. This group defines a primitive group of permutations of the Grassmann manifold
elements. This group defines a primitive group of permutations of the Grassmann manifold 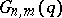 ,
, 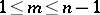 , which is maximal in
, which is maximal in  for
for 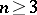 .
.
Let 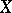 be an infinite set. The group of all permutations of
be an infinite set. The group of all permutations of 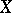 that move only a finite number of elements of
that move only a finite number of elements of 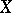 is called the finitary, or restricted, symmetric group on
is called the finitary, or restricted, symmetric group on 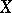 , and is denoted by
, and is denoted by  ; its subgroup of even permutations is called the finite, or restricted, alternating group on
; its subgroup of even permutations is called the finite, or restricted, alternating group on 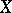 , and is denoted by
, and is denoted by  . The subgroups
. The subgroups 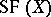 and
and 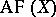 are normal in
are normal in  . More generally, let
. More generally, let 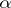 be the cardinality of
be the cardinality of 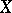 and let
and let  be an infinite cardinal; the set of permutations of
be an infinite cardinal; the set of permutations of 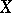 which move at most
which move at most 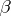 elements of
elements of 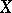 is a subgroup of
is a subgroup of 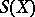 , denoted by
, denoted by  . Along with
. Along with 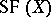 and
and 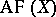 , the groups
, the groups 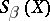 are normal subgroups in
are normal subgroups in 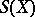 for all
for all 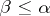 , and in fact there are no other non-trivial normal subgroups in
, and in fact there are no other non-trivial normal subgroups in 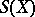 (the Schreier–Ulam–Baer theorem, see [3]).
(the Schreier–Ulam–Baer theorem, see [3]).
See also the references to Permutation of a set.
References
| [1] | L.A. Kaluzhnin, M.Kh. Klin, "On certain maximal subgroups of symmetric and alternating groups" Math. USSR Sb. , 16 : 1 (1972) pp. 95–123 Mat. Sb. , 87 : 1 (1972) pp. 91–121 |
| [2] | O. Ore, "Theory of graphs" , Amer. Math. Soc. (1962) |
| [3] | B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972) |
| [4] | V.A. Ustimenko-Bakumovskii, "Maximality of the group 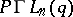 acting on subspaces of dimension acting on subspaces of dimension 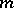 " Soviet Math. Dokl. , 19 : 3 (1978) pp. 769–772 Dokl. Akad. Nauk SSSR , 240 : 6 (1978) pp. 1305–1308 " Soviet Math. Dokl. , 19 : 3 (1978) pp. 769–772 Dokl. Akad. Nauk SSSR , 240 : 6 (1978) pp. 1305–1308 |
Comments
A complete group, i.e. a group without centre and outer automorphisms, is also called a perfect group.
See also [a1] for a result on the structure of subgroups of 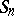 .
.
References
| [a1] | I.M. Aschbacher, L.L. Scott, "Maximal subgroups of finite groups" J. Algebra (1985) pp. 44–80 |
| [a2] | H. Wielandt, "Finite permutation groups" , Acad. Press (1964) (Translated from German) |
| [a3] | D. Passman, "Permutation groups" , Benjamin (1968) |
Symmetric group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_group&oldid=19180