Suslin hypothesis
A hypothesis that states that every linearly ordered set without first and last elements that is moreover complete, dense and satisfies the Suslin condition, is isomorphic to the real line. Here, completeness signifies the existence of a least upper bound for every non-empty bounded subset, density denotes the non-emptiness of any interval 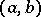 ,
, 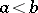 , and the Suslin condition requires that every family of pairwise-disjoint intervals is countable. The real line possesses all the properties that figure in the formulation of the Suslin hypothesis. The Suslin hypothesis thus states that the above properties of an ordered set define it completely. This hypothesis was formulated in 1920 by M.Ya. Suslin [1].
, and the Suslin condition requires that every family of pairwise-disjoint intervals is countable. The real line possesses all the properties that figure in the formulation of the Suslin hypothesis. The Suslin hypothesis thus states that the above properties of an ordered set define it completely. This hypothesis was formulated in 1920 by M.Ya. Suslin [1].
Within the framework of the system ZFC (the system ZF with the axiom of choice) it is impossible to prove or disprove the Suslin hypothesis, assuming that ZF is consistent. It follows from Gödel's axiom of constructibility (see Gödel constructive set) that the negation of the Suslin hypothesis holds. The consistency of the Suslin hypothesis with the axioms of ZFC is proved by the construction of a corresponding model, using a variant of the forcing method (iterated forcing). The addition of the continuum hypothesis to ZFC does not give either a positive or negative solution of the Suslin hypothesis.
The Suslin hypothesis and its generalizations have had a great influence on the development of axiomatic set theory. Many ideas and methods have been worked out in conjunction with it. These include Jensen's combinatorial principles 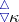 and
and 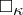 (see [4]), the theory of the fine structure of the constructible hierarchy (see [5]), Martin's axiom [7], and the iterated forcing method [2].
(see [4]), the theory of the fine structure of the constructible hierarchy (see [5]), Martin's axiom [7], and the iterated forcing method [2].
Jensen's principle 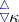 : A subset
: A subset 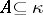 of a cardinal number
of a cardinal number 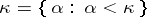 is said to be closed unbounded if it contains all its limit points
is said to be closed unbounded if it contains all its limit points 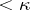 and if, for any
and if, for any 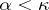 , there is a
, there is a 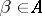 such that
such that 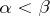 . A set
. A set 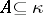 is said to be stationary if its intersection with every closed unbounded subset of a cardinal number
is said to be stationary if its intersection with every closed unbounded subset of a cardinal number 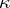 is non-empty.
is non-empty.
Jensen's principle 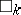 : There exists a sequence
: There exists a sequence 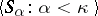 ,
, 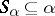 , such that for every
, such that for every 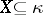 the set
the set 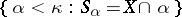 is stationary. For every regular
is stationary. For every regular 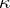 , the principle
, the principle 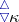 follows from the axiom of constructibility, while the negation of the Suslin hypothesis follows from
follows from the axiom of constructibility, while the negation of the Suslin hypothesis follows from 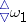 . Jensen's combinatorial principles, as well as Martin's axiom (see below), have been successfully used in topology (see [4], [6], [8]).
. Jensen's combinatorial principles, as well as Martin's axiom (see below), have been successfully used in topology (see [4], [6], [8]).
Let 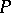 be a partially ordered set. A set
be a partially ordered set. A set 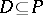 is called dense if for every
is called dense if for every 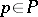 there is a
there is a 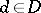 such that
such that 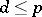 . A set
. A set 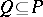 is said to be compatible if for any finite subset
is said to be compatible if for any finite subset 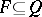 there is a
there is a 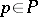 such that
such that 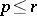 for every
for every 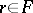 . Two elements
. Two elements 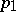 and
and 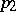 from
from 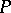 are said to be incompatible if the set
are said to be incompatible if the set 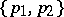 is not compatible. It is said that a partially ordered set
is not compatible. It is said that a partially ordered set 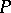 satisfies the countable anti-chain condition if every set that consists of pairwise-incompatible elements is countable. Martin's axiom (MA) states the following: If a partially ordered set
satisfies the countable anti-chain condition if every set that consists of pairwise-incompatible elements is countable. Martin's axiom (MA) states the following: If a partially ordered set 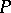 satisfies the countable anti-chain condition and if
satisfies the countable anti-chain condition and if 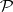 is a family of dense subsets of cardinality less than
is a family of dense subsets of cardinality less than 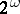 , then there is a compatible set
, then there is a compatible set 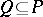 such that for every
such that for every 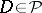 the intersection
the intersection 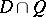 is non-empty.
is non-empty.
In the presence of the continuum hypothesis (CH), Martin's axiom can be proved. The most interesting results are obtained by a combination of Martin's axiom (MA) and the negation of the continuum hypothesis 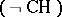 . The principle
. The principle 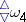 contradicts the combination
contradicts the combination 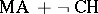 , since
, since 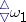 implies CH. It often turns out that a result that can be inferred from
implies CH. It often turns out that a result that can be inferred from 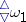 will be disproved under the assumption
will be disproved under the assumption 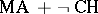 . This is, e.g., the case with the Suslin hypothesis. Indeed,
. This is, e.g., the case with the Suslin hypothesis. Indeed, 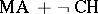 implies the Suslin hypothesis, while
implies the Suslin hypothesis, while 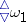 implies the negation of the Suslin hypothesis.
implies the negation of the Suslin hypothesis.
The combination 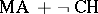 is compatible with ZFC if ZF is consistent.
is compatible with ZFC if ZF is consistent.
References
| [1] | M. [M.Ya. Suslin] Souslin, "Problème 3" Fundam. Math. , 1 (1920) pp. 223 |
| [2] | K.J. Devlin, H. Johnsbråten, "The Souslin problem" , Lect. notes in math. , 405 , Springer (1974) |
| [3] | T.J. Jech, "Lectures in set theory: with particular emphasis on the method of forcing" , Lect. notes in math. , 217 , Springer (1971) |
| [4] | J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. Chapts. B4-B7 |
| [5] | K.J. Devlin, "Aspects of constructibility" , Lect. notes in math. , 354 , Springer (1973) |
| [6] | V.V. Fedorchuk, "Completely closed mappings and the compatibility of certain general topology theorems with the axioms of set theory" Mat. Sb. , 99 : 1 (1976) pp. 3–33 (In Russian) |
| [7] | D.A. Martin, R. Solovay, "Internal Cohen extensions" Ann. Math. Logic , 2 (1970) pp. 143–178 |
| [8] | V.I. Malykhin, "Topology and forcing" Russian Math. Surveys , 38 : 1 (1983) pp. 77–136 Uspekhi Mat. Nauk , 38 : 1 (1983) pp. 69–118 |
Comments
Jensen's combinatorial principles  and
and  are called diamond and square, respectively. The countable anti-chain condition is sometimes called the countable chain condition, and is then also abbreviated to ccc.
are called diamond and square, respectively. The countable anti-chain condition is sometimes called the countable chain condition, and is then also abbreviated to ccc.
References
| [a1] | K.J. Devlin, "Constructibility" , Springer (1984) |
| [a2] | D.H. Fremlin, "Consequences of Martin's axiom" , Cambridge Univ. Press (1984) |
| [a3] | T.J. Jech, "Multiple forcing" , Cambridge Univ. Press (1986) |
| [a4] | T.J. Jech, "Set theory" , Acad. Press (1978) (Translated from German) |
| [a5] | K. Kunen, "Set theory, an introduction to independence proofs" , North-Holland (1980) |
Suslin hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Suslin_hypothesis&oldid=18257