Namespaces
Variants
Actions

Difference between revisions of "Strip method (integral equations)"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48874 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
 
−
s0905101.png
 
−
$#A+1 = 19 n = 0
 
−
$#C+1 = 19 : ~/encyclopedia/old_files/data/S090/S.0900510 Strip method (integral equations)
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
−
 
−
{{TEX|auto}}
 
−
{{TEX|done}}
 
−
 
 
A method for the approximate solution of one-dimensional Fredholm integral equations of the second kind (cf. also [[Fredholm equation|Fredholm equation]]; [[Fredholm equation, numerical methods|Fredholm equation, numerical methods]]), based on replacing the kernel in a special way by a degenerate kernel, evaluating the resolvent of the degenerate equation and then improving the approximate solution through the use of a rapidly-convergent iterative algorithm.
 
A method for the approximate solution of one-dimensional Fredholm integral equations of the second kind (cf. also [[Fredholm equation|Fredholm equation]]; [[Fredholm equation, numerical methods|Fredholm equation, numerical methods]]), based on replacing the kernel in a special way by a degenerate kernel, evaluating the resolvent of the degenerate equation and then improving the approximate solution through the use of a rapidly-convergent iterative algorithm.
  
 
Let the original integral equation be written as
 
Let the original integral equation be written as
  
−
$$ \tag{1 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905101.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
−
\phi ( x) - \lambda \int\limits _ { a } ^ { b }  K ( x , s ) \phi ( s)  d s  = f ( x) .
 
−
$$
 
  
 
To construct the degenerate kernel, divide the square
 
To construct the degenerate kernel, divide the square
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905102.png" /></td> </tr></table>
−
\{ a \leq  x \leq  b , a \leq  s \leq  b \}
 
−
$$
 
  
−
into $  N $
+
into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905103.png" /> strips
−
strips
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905104.png" /></td> </tr></table>
−
\left \{ b-  
 
−
\frac{a}{N}
 
−
i \leq  x \leq  b-
 
−
\frac{a}{N}
 
  
−
( i + 1 ) , a \leq  s \leq  b \right \} ,\ \
+
In each strip, say the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905105.png" />-th, the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905106.png" /> is approximated in the mean square, or uniformly, by functions
−
i = 0 \dots N - 1 .
 
−
$$
 
  
−
In each strip, say the  $  i $-
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905107.png" /></td> </tr></table>
−
th, the function  $  K ( x , s ) $
 
−
is approximated in the mean square, or uniformly, by functions
 
−
 
 
−
$$
 
−
K _ {i} ( x , s )  = C _ {i} ( x) + P _ {i} ( x) Q _ {i} ( s) .
 
−
$$
 
  
 
In the simplest case,
 
In the simplest case,
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905108.png" /></td> </tr></table>
−
K _ {i} ( x , s )  = K ( \xi _ {i} , s ) ,\ \
 
−
\xi _ {i} \in \left [ b-
 
−
\frac{a}{N}
 
−
i , b-
 
−
\frac{a}{N}
 
−
( i + 1 ) \right ] .
 
−
$$
 
  
−
The function $  K _ {i} ( x , s ) $
+
The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s0905109.png" /> is now used to construct a [[Degenerate kernel|degenerate kernel]]:
−
is now used to construct a [[Degenerate kernel|degenerate kernel]]:
 
  
−
$$ \tag{2 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051010.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
−
K _ {N} ( x , s )  = \sum _ { i= } 0 ^ { N- }  1 [ \widehat{C}  _ {i} ( x) +
 
−
\widehat{P}  _ {i} ( x) Q _ {i} ( s)] ,
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051011.png" /></td> </tr></table>
−
\widehat{P}  _ {i} ( x)  = \left \{
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051012.png" /></td> </tr></table>
−
\widehat{C}  _ {i} ( x)  = \left \{
 
  
−
The solution of the equation with the degenerate kernel (2) approximates the solution of equation (1), generally, the better the larger the number $  N $
+
The solution of the equation with the degenerate kernel (2) approximates the solution of equation (1), generally, the better the larger the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051013.png" /> of strips and the better the approximation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051014.png" /> in each strip is. The approximate solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051015.png" /> can be further improved by using the iterative algorithm
−
of strips and the better the approximation of $  K ( x , s ) $
 
−
in each strip is. The approximate solution $  \phi _ {0} ( x) $
 
−
can be further improved by using the iterative algorithm
 
  
−
$$ \tag{3 }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051016.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table>
−
\phi _ {k} ( x) - \lambda \int\limits _ { a } ^ { b }  K _ {N} ( x , s ) \phi _ {k} ( s) d s =
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051017.png" /></td> </tr></table>
−
= \
 
−
f ( x) + \lambda \int\limits _ { a } ^ { b }  [ K ( x , s ) -
 
−
K _ {N} ( x , s ) ] \phi _ {k-} 1 ( s)  d s .
 
−
$$
 
  
−
The iterations (3) converge in the mean square, or uniformly, to the solution of equation (1), provided the kernels $  K _ {N} ( x , s ) $
+
The iterations (3) converge in the mean square, or uniformly, to the solution of equation (1), provided the kernels <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051018.png" /> approach <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090510/s09051019.png" />.
−
approach $  K ( x , s ) $.
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  G.N. Polozhii,  P.I. Chalenko,  "The strip method for solving integral equations"  ''Dop. Akad. Nauk UkrSSR'' :  4  (1962)  pp. 427–431  (In Ukrainian)  ((English abstract.))</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  G.N. Polozhii,  P.I. Chalenko,  "The strip method for solving integral equations"  ''Dop. Akad. Nauk UkrSSR'' :  4  (1962)  pp. 427–431  (In Ukrainian)  ((English abstract.))</TD></TR></table>
 +
 +
  
 
====Comments====
 
====Comments====

Revision as of 14:53, 7 June 2020

A method for the approximate solution of one-dimensional Fredholm integral equations of the second kind (cf. also Fredholm equation; Fredholm equation, numerical methods), based on replacing the kernel in a special way by a degenerate kernel, evaluating the resolvent of the degenerate equation and then improving the approximate solution through the use of a rapidly-convergent iterative algorithm.

Let the original integral equation be written as

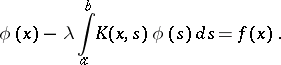(1)

To construct the degenerate kernel, divide the square

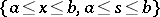into 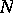strips

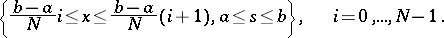In each strip, say the 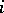-th, the function 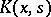is approximated in the mean square, or uniformly, by functions

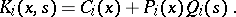In the simplest case,

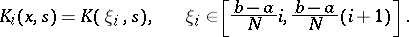The function 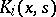is now used to construct a degenerate kernel:

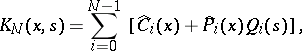(2)

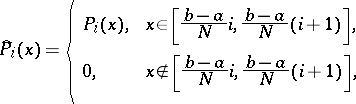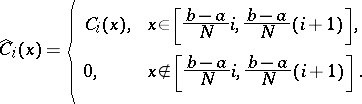The solution of the equation with the degenerate kernel (2) approximates the solution of equation (1), generally, the better the larger the number 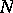of strips and the better the approximation of in each strip is. The approximate solution 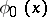can be further improved by using the iterative algorithm

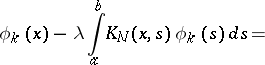(3)

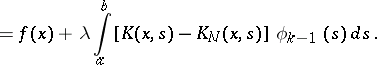The iterations (3) converge in the mean square, or uniformly, to the solution of equation (1), provided the kernels 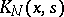approach .

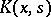References

[1] G.N. Polozhii, P.I. Chalenko, "The strip method for solving integral equations" Dop. Akad. Nauk UkrSSR : 4 (1962) pp. 427–431 (In Ukrainian) ((English abstract.))


Comments

Excellent surveys on the numerical solution of Fredholm equations of the second kind can be found in [a1] and [a2]; the strip method is not mentioned there, although other degenerate kernel methods are discussed, cf. also Degenerate kernels, method of.

References

[a1] K.E. Atkinson, "A survey of numerical methods for the solution of Fredholm integral equations of the second kind" , SIAM (1976)
[a2] C.T.H. Baker, "The numerical treatment of integral equations" , Clarendon Press (1977) pp. Chapt. 4
How to Cite This Entry:
Strip method (integral equations). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strip_method_(integral_equations)&oldid=49451
This article was adapted from an original article by A.B. Bakushinskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Strip_method_(integral_equations)&oldid=49451"