Stochastic matrix
2020 Mathematics Subject Classification: Primary: 15B51 Secondary: 60J10 [MSN][ZBL]
A square (possibly infinite) matrix  with non-negative elements, for which
with non-negative elements, for which
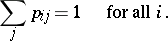 |
The set of all stochastic matrices of order  is the convex hull of the set of
is the convex hull of the set of  stochastic matrices consisting of zeros and ones. Any stochastic matrix
stochastic matrices consisting of zeros and ones. Any stochastic matrix  can be considered as the matrix of transition probabilities of a discrete Markov chain
can be considered as the matrix of transition probabilities of a discrete Markov chain  .
.
The absolute values of the eigenvalues of stochastic matrices do not exceed 1; 1 is an eigenvalue of any stochastic matrix. If a stochastic matrix  is indecomposable (the Markov chain
is indecomposable (the Markov chain  has one class of positive states), then 1 is a simple eigenvalue of
has one class of positive states), then 1 is a simple eigenvalue of  (i.e. it has multiplicity 1); in general, the multiplicity of the eigenvalue 1 coincides with the number of classes of positive states of the Markov chain
(i.e. it has multiplicity 1); in general, the multiplicity of the eigenvalue 1 coincides with the number of classes of positive states of the Markov chain 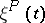 . If a stochastic matrix is indecomposable and if the class of positive states of the Markov chain has period
. If a stochastic matrix is indecomposable and if the class of positive states of the Markov chain has period 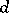 , then the set of all eigenvalues of
, then the set of all eigenvalues of  , as a set of points in the complex plane, is mapped onto itself by rotation through an angle
, as a set of points in the complex plane, is mapped onto itself by rotation through an angle 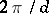 . When
. When 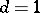 , the stochastic matrix
, the stochastic matrix 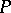 and the Markov chain
and the Markov chain 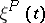 are called aperiodic.
are called aperiodic.
The left eigenvectors  of
of  of finite order, corresponding to the eigenvalue
of finite order, corresponding to the eigenvalue 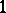 :
:
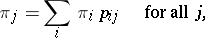 | (1) |
and satisfying the conditions 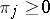 ,
,  , define the stationary distributions of the Markov chain
, define the stationary distributions of the Markov chain 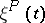 ; in the case of an indecomposable matrix
; in the case of an indecomposable matrix 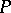 , the stationary distribution is unique.
, the stationary distribution is unique.
If  is an indecomposable aperiodic stochastic matrix of finite order, then the following limit exists:
is an indecomposable aperiodic stochastic matrix of finite order, then the following limit exists:
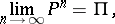 | (2) |
where 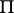 is the matrix all rows of which coincide with the vector
is the matrix all rows of which coincide with the vector  (see also Markov chain, ergodic; for infinite stochastic matrices
(see also Markov chain, ergodic; for infinite stochastic matrices  , the system of equations (1) may have no non-zero non-negative solutions that satisfy the condition
, the system of equations (1) may have no non-zero non-negative solutions that satisfy the condition  ; in this case
; in this case 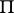 is the zero matrix). The rate of convergence in (2) can be estimated by a geometric progression with any exponent
is the zero matrix). The rate of convergence in (2) can be estimated by a geometric progression with any exponent 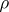 that has absolute value greater than the absolute values of all the eigenvalues of
that has absolute value greater than the absolute values of all the eigenvalues of  other than 1.
other than 1.
If 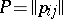 is a stochastic matrix of order
is a stochastic matrix of order  , then any of its eigenvalues
, then any of its eigenvalues  satisfies the inequality (see [MM]):
satisfies the inequality (see [MM]):
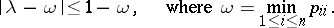 |
The union 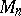 of the sets of eigenvalues of all stochastic matrices of order
of the sets of eigenvalues of all stochastic matrices of order  has been described (see [Ka]).
has been described (see [Ka]).
A stochastic matrix  that satisfies the extra condition
that satisfies the extra condition
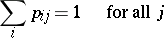 |
is called a doubly-stochastic matrix. The set of doubly-stochastic matrices of order  is the convex hull of the set of
is the convex hull of the set of  permutation matrices of order
permutation matrices of order  (i.e. doubly-stochastic matrices consisting of zeros and ones). A finite Markov chain
(i.e. doubly-stochastic matrices consisting of zeros and ones). A finite Markov chain 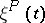 with a doubly-stochastic matrix
with a doubly-stochastic matrix  has the uniform stationary distribution.
has the uniform stationary distribution.
References
| [G] | F.R. Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) MR1657129 MR0107649 MR0107648 Zbl 0927.15002 Zbl 0927.15001 Zbl 0085.01001 |
| [B] | R. Bellman, "Introduction to matrix analysis" , McGraw-Hill (1960) MR0122820 Zbl 0124.01001 |
| [MM] | M. Marcus, H. Minc, "A survey of matrix theory and matrix inequalities" , Allyn & Bacon (1964) MR0162808 Zbl 0126.02404 |
| [Ka] | F.I. Karpelevich, "On the characteristic roots of matrices with non-negative entries" Izv. Akad. Nauk SSSR Ser. Mat. , 15 (1951) pp. 361–383 (In Russian) |
Comments
Given a real 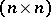 -matrix
-matrix 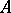 with non-negative entries, the question arises whether there are invertible positive diagonal matrices
with non-negative entries, the question arises whether there are invertible positive diagonal matrices 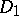 and
and 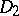 such that
such that 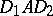 is a doubly-stochastic matrix, and to what extent the
is a doubly-stochastic matrix, and to what extent the 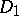 and
and 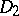 are unique. Such theorems are known as
are unique. Such theorems are known as  -theorems. They are of interest in telecommunications and statistics, [C], [F], [Kr].
-theorems. They are of interest in telecommunications and statistics, [C], [F], [Kr].
A matrix 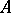 is fully decomposable if there do not exist permutation matrices
is fully decomposable if there do not exist permutation matrices  and
and 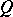 such that
such that
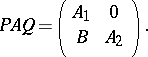 |
A  -matrix is fully indecomposable if it is non-zero.
-matrix is fully indecomposable if it is non-zero.
Then for a non-negative square matrix 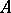 there exist positive diagonal matrices
there exist positive diagonal matrices 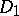 and
and  such that
such that 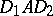 is doubly stochastic if and only if there exist permutation matrices
is doubly stochastic if and only if there exist permutation matrices 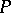 and
and 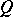 such that
such that 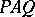 is a direct sum of fully indecomposable matrices [SK], [BPS].
is a direct sum of fully indecomposable matrices [SK], [BPS].
References
| [SK] | R. Sinkhorn, P. Knopp, "Concerning nonnegative matrices and doubly stochastic matrices" Pacific J. Math. , 21 (1967) pp. 343–348 MR0210731 Zbl 0152.01403 |
| [BPS] | R.A. Brualdi, S.V. Parter, H. Schneider, "The diagonal equivalence of a nonnegative matrix to a stochastic matrix" J. Math. Anal. Appl. , 16 (1966) pp. 31–50 MR0206019 Zbl 0231.15017 |
| [F] | S. Fienberg, "An iterative procedure for estimation in contingency tables" Ann. Math. Stat. , 41 (1970) pp. 907–917 MR0266394 Zbl 0198.23401 |
| [Kr] | R.S. Krupp, "Properties of Kruithof's projection method" Bell Systems Techn. J. , 58 (1979) pp. 517–538 |
| [C] | I. Csiszár, "I-divergence geometry of probability distributions and minimization problems" Ann. Probab. , 3 (1975) pp. 146–158 MR0365798 Zbl 0318.60013 |
| [Nu] | R.D. Nussbaum, "Iterated nonlinear maps and Hilbert's projective method II" Memoirs Amer. Math. Soc. , 401 (1989) |
| [Ne] | M.F. Neuts, "Structured stochastic matrices of 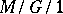 type and their applications" , M. Dekker (1989) MR1010040 Zbl 0695.60088 type and their applications" , M. Dekker (1989) MR1010040 Zbl 0695.60088
|
| [S] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) MR2209438 Zbl 0471.60001 |
Stochastic matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_matrix&oldid=26956