Difference between revisions of "Stochastic matrix"
(TeXed the first few paragraphs) |
(TeX done) |
||
| Line 1: | Line 1: | ||
{{MSC|15B51|60J10}} | {{MSC|15B51|60J10}} | ||
| + | {{TEX|done}} | ||
| + | [[Category:Special matrices]] [[Category:Markov chains]] | ||
| − | [[ | + | A stochastic matrix is a square (possibly infinite) matrix |
| − | [[ | + | $P=[p_{ij}]$ with non-negative elements, for which |
| + | $$ | ||
| + | \sum_j p_{ij} = 1 \quad \text{for all $i$.} | ||
| + | $$ | ||
| + | The set of all stochastic matrices of | ||
| + | order $n$ is the convex hull of the set of $n^n$ stochastic matrices | ||
| + | consisting of zeros and ones. Any stochastic matrix $P$ can be | ||
| + | considered as the | ||
| + | [[Matrix of transition probabilities|matrix of transition | ||
| + | probabilities]] of a discrete | ||
| + | [[Markov chain|Markov chain]] $\xi^P(t)$. | ||
| − | + | The absolute values of the eigenvalues of stochastic matrices do not | |
| + | exceed 1; 1 is an eigenvalue of any stochastic matrix. If a stochastic | ||
| + | matrix $P$ is indecomposable (the Markov chain $\xi^P(t)$ has one | ||
| + | class of positive states), then 1 is a simple eigenvalue of $P$ | ||
| + | (i.e. it has multiplicity 1); in general, the multiplicity of the | ||
| + | eigenvalue 1 coincides with the number of classes of positive states | ||
| + | of the Markov chain $\xi^P(t)$. If a stochastic matrix is | ||
| + | indecomposable and if the class of positive states of the Markov chain | ||
| + | has period $d$, then the set of all eigenvalues of $P$, as a set of | ||
| + | points in the complex plane, is mapped onto itself by rotation through | ||
| + | an angle $2\pi/d$. When $d=1$, the stochastic matrix $P$ and the | ||
| + | Markov chain $\xi^P(t)$ are called aperiodic. | ||
| + | |||
| + | The left eigenvectors $\pi = \{\pi_j\}$ of $P$ of finite order, | ||
| + | corresponding to the eigenvalue 1: | ||
| + | \begin{equation} | ||
| + | \label{eq1} | ||
| + | \pi_j = \sum_i \pi_i p_{ij} | ||
| + | \quad \text{for all $j$,} | ||
| + | \end{equation} | ||
| + | and satisfying the conditions $\pi_j \geq | ||
| + | 0$, $\sum_j\pi_j = 1$, define the stationary distributions of the | ||
| + | Markov chain $\xi^P(t)$; in the case of an indecomposable matrix $P$, | ||
| + | the stationary distribution is unique. | ||
| + | |||
| + | If $P$ is an indecomposable aperiodic stochastic matrix of finite | ||
| + | order, then the following limit exists: | ||
| + | \begin{equation} | ||
| + | \label{eq2} | ||
| + | \lim_{n\rightarrow\infty} P^n = \Pi, | ||
| + | \end{equation} | ||
| + | where $\Pi$ is the matrix | ||
| + | all rows of which coincide with the vector $\pi$ (see also | ||
| + | [[Markov chain, ergodic|Markov chain, ergodic]]; for infinite | ||
| + | stochastic matrices $P$, the system of equations \ref{eq1} may have no | ||
| + | non-zero non-negative solutions that satisfy the condition | ||
| + | $\sum_j \pi_j < \infty$; in | ||
| + | this case $\Pi$ is the zero matrix). The rate of convergence in \ref{eq2} can | ||
| + | be estimated by a geometric progression with any exponent $\rho$ that has | ||
| + | absolute value greater than the absolute values of all the eigenvalues | ||
| + | of $P$ other than 1. | ||
| + | |||
| + | If $P = [p_{ij}]$ is a stochastic matrix of order $n$, then any of its | ||
| + | eigenvalues $\lambda$ satisfies the inequality (see {{Cite|MM}}): | ||
$$ | $$ | ||
| − | \ | + | \left| \lambda - \omega \right| \leq 1-\omega, \quad |
| + | \text{where $\omega = \min_{1 \leq i \leq n} p_{ii}.$} | ||
$$ | $$ | ||
| − | The | + | The union $M_n$ of the sets of eigenvalues of all stochastic matrices of |
| + | order $n$ has been described (see {{Cite|Ka}}). | ||
| − | + | A stochastic matrix $P=[p_{ij}]$ that satisfies the extra condition | |
| − | |||
| − | |||
$$ | $$ | ||
| − | + | \sum_i p_{ij} = 1 \quad \text{for all $j$} | |
$$ | $$ | ||
| − | + | is called a doubly-stochastic matrix. The set of doubly-stochastic | |
| − | + | matrices of order $n$ is the convex hull of the set of $n!$ permutation | |
| − | + | matrices of order $n$ (i.e. doubly-stochastic matrices consisting of | |
| − | + | zeros and ones). A finite Markov chain $\xi^P(t)$ with a doubly-stochastic | |
| − | + | matrix $P$ has the uniform stationary distribution. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | is called a doubly-stochastic matrix. The set of doubly-stochastic matrices of order | ||
====References==== | ====References==== | ||
| Line 48: | Line 89: | ||
====Comments==== | ====Comments==== | ||
| − | Given a real | + | Given a real $n\times n$ matrix $A$ with non-negative |
| + | entries, the question arises whether there are invertible positive | ||
| + | diagonal matrices $D_1$ and $D_2$ such that $D_1AD_2$ is a doubly-stochastic | ||
| + | matrix, and to what extent the $D_1$ and $D_2$ are unique. Such theorems | ||
| + | are known as $DAD$-theorems. They are of interest in telecommunications | ||
| + | and statistics, {{Cite|C}}, {{Cite|F}}, {{Cite|Kr}}. | ||
| − | A matrix | + | A matrix $A$ is fully decomposable if there do not exist permutation |
| − | + | matrices $P$ and $Q$ such that | |
| − | + | $$ | |
| − | + | PAQ = | |
| − | A | + | \left[ |
| + | \begin{array}{cc} | ||
| + | A_1 & 0 \\ | ||
| + | B & A_2 | ||
| + | \end{array} | ||
| + | \right]. | ||
| + | $$ | ||
| + | A $1 \times 1$ matrix is fully indecomposable if it is non-zero. | ||
| − | Then for a non-negative square matrix | + | Then for a non-negative square matrix $A$ there exist positive |
| + | diagonal matrices $D_1$ and $D_2$ such that $D_1AD_2$ is doubly stochastic if | ||
| + | and only if there exist permutation matrices $P$ and $Q$ such that $PAQ$ | ||
| + | is a direct sum of fully indecomposable matrices {{Cite|SK}}, | ||
| + | {{Cite|BPS}}. | ||
====References==== | ====References==== | ||
Revision as of 19:35, 30 May 2012
2020 Mathematics Subject Classification: Primary: 15B51 Secondary: 60J10 [MSN][ZBL]
A stochastic matrix is a square (possibly infinite) matrix $P=[p_{ij}]$ with non-negative elements, for which $$ \sum_j p_{ij} = 1 \quad \text{for all $i$.} $$ The set of all stochastic matrices of order $n$ is the convex hull of the set of $n^n$ stochastic matrices consisting of zeros and ones. Any stochastic matrix $P$ can be considered as the matrix of transition probabilities of a discrete Markov chain $\xi^P(t)$.
The absolute values of the eigenvalues of stochastic matrices do not exceed 1; 1 is an eigenvalue of any stochastic matrix. If a stochastic matrix $P$ is indecomposable (the Markov chain $\xi^P(t)$ has one class of positive states), then 1 is a simple eigenvalue of $P$ (i.e. it has multiplicity 1); in general, the multiplicity of the eigenvalue 1 coincides with the number of classes of positive states of the Markov chain $\xi^P(t)$. If a stochastic matrix is indecomposable and if the class of positive states of the Markov chain has period $d$, then the set of all eigenvalues of $P$, as a set of points in the complex plane, is mapped onto itself by rotation through an angle $2\pi/d$. When $d=1$, the stochastic matrix $P$ and the Markov chain $\xi^P(t)$ are called aperiodic.
The left eigenvectors $\pi = \{\pi_j\}$ of $P$ of finite order, corresponding to the eigenvalue 1: \begin{equation} \label{eq1} \pi_j = \sum_i \pi_i p_{ij} \quad \text{for all '"`UNIQ-MathJax22-QINU`"',} \end{equation} and satisfying the conditions $\pi_j \geq 0$, $\sum_j\pi_j = 1$, define the stationary distributions of the Markov chain $\xi^P(t)$; in the case of an indecomposable matrix $P$, the stationary distribution is unique.
If $P$ is an indecomposable aperiodic stochastic matrix of finite order, then the following limit exists: \begin{equation} \label{eq2} \lim_{n\rightarrow\infty} P^n = \Pi, \end{equation} where $\Pi$ is the matrix all rows of which coincide with the vector $\pi$ (see also Markov chain, ergodic; for infinite stochastic matrices $P$, the system of equations \ref{eq1} may have no non-zero non-negative solutions that satisfy the condition $\sum_j \pi_j < \infty$; in this case $\Pi$ is the zero matrix). The rate of convergence in \ref{eq2} can be estimated by a geometric progression with any exponent $\rho$ that has absolute value greater than the absolute values of all the eigenvalues of $P$ other than 1.
If $P = [p_{ij}]$ is a stochastic matrix of order $n$, then any of its eigenvalues $\lambda$ satisfies the inequality (see [MM]): $$ \left| \lambda - \omega \right| \leq 1-\omega, \quad \text{where $\omega = \min_{1 \leq i \leq n} p_{ii}.$} $$ The union $M_n$ of the sets of eigenvalues of all stochastic matrices of order $n$ has been described (see [Ka]).
A stochastic matrix $P=[p_{ij}]$ that satisfies the extra condition $$ \sum_i p_{ij} = 1 \quad \text{for all $j$} $$ is called a doubly-stochastic matrix. The set of doubly-stochastic matrices of order $n$ is the convex hull of the set of $n!$ permutation matrices of order $n$ (i.e. doubly-stochastic matrices consisting of zeros and ones). A finite Markov chain $\xi^P(t)$ with a doubly-stochastic matrix $P$ has the uniform stationary distribution.
References
| [G] | F.R. Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) MR1657129 MR0107649 MR0107648 Zbl 0927.15002 Zbl 0927.15001 Zbl 0085.01001 |
| [B] | R. Bellman, "Introduction to matrix analysis" , McGraw-Hill (1960) MR0122820 Zbl 0124.01001 |
| [MM] | M. Marcus, H. Minc, "A survey of matrix theory and matrix inequalities" , Allyn & Bacon (1964) MR0162808 Zbl 0126.02404 |
| [Ka] | F.I. Karpelevich, "On the characteristic roots of matrices with non-negative entries" Izv. Akad. Nauk SSSR Ser. Mat. , 15 (1951) pp. 361–383 (In Russian) |
Comments
Given a real $n\times n$ matrix $A$ with non-negative entries, the question arises whether there are invertible positive diagonal matrices $D_1$ and $D_2$ such that $D_1AD_2$ is a doubly-stochastic matrix, and to what extent the $D_1$ and $D_2$ are unique. Such theorems are known as $DAD$-theorems. They are of interest in telecommunications and statistics, [C], [F], [Kr].
A matrix $A$ is fully decomposable if there do not exist permutation matrices $P$ and $Q$ such that $$ PAQ = \left[ \begin{array}{cc} A_1 & 0 \\ B & A_2 \end{array} \right]. $$ A $1 \times 1$ matrix is fully indecomposable if it is non-zero.
Then for a non-negative square matrix $A$ there exist positive diagonal matrices $D_1$ and $D_2$ such that $D_1AD_2$ is doubly stochastic if and only if there exist permutation matrices $P$ and $Q$ such that $PAQ$ is a direct sum of fully indecomposable matrices [SK], [BPS].
References
| [SK] | R. Sinkhorn, P. Knopp, "Concerning nonnegative matrices and doubly stochastic matrices" Pacific J. Math. , 21 (1967) pp. 343–348 MR0210731 Zbl 0152.01403 |
| [BPS] | R.A. Brualdi, S.V. Parter, H. Schneider, "The diagonal equivalence of a nonnegative matrix to a stochastic matrix" J. Math. Anal. Appl. , 16 (1966) pp. 31–50 MR0206019 Zbl 0231.15017 |
| [F] | S. Fienberg, "An iterative procedure for estimation in contingency tables" Ann. Math. Stat. , 41 (1970) pp. 907–917 MR0266394 Zbl 0198.23401 |
| [Kr] | R.S. Krupp, "Properties of Kruithof's projection method" Bell Systems Techn. J. , 58 (1979) pp. 517–538 |
| [C] | I. Csiszár, "I-divergence geometry of probability distributions and minimization problems" Ann. Probab. , 3 (1975) pp. 146–158 MR0365798 Zbl 0318.60013 |
| [Nu] | R.D. Nussbaum, "Iterated nonlinear maps and Hilbert's projective method II" Memoirs Amer. Math. Soc. , 401 (1989) |
| [Ne] | M.F. Neuts, "Structured stochastic matrices of 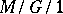 type and their applications" , M. Dekker (1989) MR1010040 Zbl 0695.60088 type and their applications" , M. Dekker (1989) MR1010040 Zbl 0695.60088
|
| [S] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) MR2209438 Zbl 0471.60001 |
Stochastic matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_matrix&oldid=26961