Difference between revisions of "Stiefel manifold"
Ulf Rehmann (talk | contribs) m (Undo revision 48838 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0877701.png | ||
| + | $#A+1 = 67 n = 5 | ||
| + | $#C+1 = 67 : ~/encyclopedia/old_files/data/S087/S.0807770 Stiefel manifold | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''(real)'' | ''(real)'' | ||
| − | The manifold | + | The manifold $ V _ {n,k} $ |
| + | of orthonormal $ k $- | ||
| + | frames in an $ n $- | ||
| + | dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold $ W _ {n,k} $ | ||
| + | and a quaternion Stiefel manifold $ X _ {n,k} $. | ||
| + | Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups $ O( n) $, | ||
| + | $ U( n) $ | ||
| + | and $ \mathop{\rm Sp} ( n) $, | ||
| + | respectively. In particular, $ V _ {n,1} = S ^ {n-} 1 $, | ||
| + | $ W _ {n,1} = S ^ {2n-} 1 $, | ||
| + | $ X _ {n,1} = S ^ {4n-} 1 $ | ||
| + | are the spheres, the Stiefel manifold $ V _ {n,2} $ | ||
| + | is the manifold of unit vectors tangent to $ S ^ {n-} 1 $, | ||
| + | the Stiefel manifolds $ V _ {n,n} $, | ||
| + | $ W _ {n,n} $, | ||
| + | $ X _ {n,n} $ | ||
| + | are identified with the groups $ O( n) $, | ||
| + | $ U( n) $, | ||
| + | $ \mathop{\rm Sp} ( n) $, | ||
| + | and $ V _ {n,n-} 1 $— | ||
| + | with the group $ \mathop{\rm SO} ( n) $. | ||
| + | Sometimes non-compact Stiefel manifolds, consisting of all possible $ k $- | ||
| + | frames in $ \mathbf R ^ {n} $, | ||
| + | $ \mathbf C ^ {n} $ | ||
| + | or $ \mathbf H ^ {n} $, | ||
| + | are considered. | ||
These manifolds were introduced by E. Stiefel [[#References|[1]]] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [[#References|[1]]], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [[#References|[2]]], [[#References|[3]]]). In particular, | These manifolds were introduced by E. Stiefel [[#References|[1]]] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [[#References|[1]]], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [[#References|[2]]], [[#References|[3]]]). In particular, | ||
| − | + | $$ | |
| + | H ^ \star ( W _ {n,k} , \mathbf Z ) = \Lambda _ {\mathbf Z} ( x _ {2n-} 1 , x _ {2n-} 3 \dots x _ {2(} n- k)+ 1 ), | ||
| + | $$ | ||
| − | + | $$ | |
| + | H ^ \star ( X _ {n,k} , \mathbf Z ) = \Lambda _ {\mathbf Z} ( x _ {4n-} 1 , x _ {4n-} 5 \dots x _ {4(} n- k)+ 3 ), | ||
| + | $$ | ||
| − | + | $ H ^ \star ( V _ {n,k} , \mathbf Z _ {2} ) $ | |
| + | is a commutative algebra with generators $ x _ {n-} k \dots x _ {n-} 1 $ | ||
| + | and relations | ||
| − | + | $$ | |
| + | x _ {i} x _ {j} = \left \{ | ||
| − | + | \begin{array}{lll} | |
| + | x _ {i+} j & \textrm{ for } &i+ j \leq n- 1, \\ | ||
| + | 0 & \textrm{ for } &i+ j > n- 1 \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
| − | + | (everywhere above, $ x _ {l} $ | |
| + | denotes an element of order $ l $). | ||
| + | Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding $ n- k- 1 $, | ||
| + | $ 2( n- k) $ | ||
| + | and $ 4( n- k)+ 2 $, | ||
| + | respectively. Moreover, | ||
| + | |||
| + | $$ | ||
| + | \pi _ {n-} k ( V _ {n,k} ) \cong \left \{ | ||
| + | |||
| + | \begin{array}{ll} | ||
| + | \mathbf Z & \textrm{ if } k= 1 \textrm{ or } n- k \textrm{ is even }, \\ | ||
| + | \mathbf Z _ {2} & \textrm{ if } k> 1 \textrm{ or } n- k \textrm{ is odd } ; \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right .$$ | ||
| + | |||
| + | $$ | ||
| + | \pi _ {2(} n- k)+ 1 ( W _ {n,k} ) \cong \pi _ {4(} n- k)+ 3 ( X _ {n,k} ) \cong \mathbf Z . | ||
| + | $$ | ||
The computation of other homotopy groups of Stiefel manifolds is discussed in [[#References|[5]]]. | The computation of other homotopy groups of Stiefel manifolds is discussed in [[#References|[5]]]. | ||
| Line 23: | Line 89: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Stiefel, "Richtungsfelder und Fernparallelismus in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777038.png" />-dimensionalen Mannigfaltigkeiten" ''Comm. Math. Helv.'' , '''8''' : 4 (1935–1936) pp. 305–353</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, , ''Fibre spaces and their applications'' , Moscow (1958) pp. 163–246 (In Russian; translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom.'' (1971) pp. 71–122</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Stiefel, "Richtungsfelder und Fernparallelismus in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777038.png" />-dimensionalen Mannigfaltigkeiten" ''Comm. Math. Helv.'' , '''8''' : 4 (1935–1936) pp. 305–353</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, , ''Fibre spaces and their applications'' , Moscow (1958) pp. 163–246 (In Russian; translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom.'' (1971) pp. 71–122</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
For homotopy groups of Stiefel manifolds see also . | For homotopy groups of Stiefel manifolds see also . | ||
| − | Another (and better) frequently used notation for the Stiefel manifolds | + | Another (and better) frequently used notation for the Stiefel manifolds $ V _ {n,k } $, |
| + | $ W _ {n,k } $ | ||
| + | and $ X _ {n,k } $ | ||
| + | is $ V _ {k} ( \mathbf R ^ {n} ) $, | ||
| + | $ V _ {k} ( \mathbf C ^ {n} ) $, | ||
| + | $ V _ {k} ( \mathbf H ^ {n} ) $, | ||
| + | generalizing to $ V _ {k} ( E ) $ | ||
| + | where $ E $ | ||
| + | is an appropriate vector space. | ||
As homogeneous spaces these Stiefel manifolds are equal to, respectively, | As homogeneous spaces these Stiefel manifolds are equal to, respectively, | ||
| − | + | $$ | |
| + | V _ {k} ( \mathbf R ^ {n} ) = \ | ||
| + | O( | ||
| + | \frac{n)}{O(} | ||
| + | n- k) = \ | ||
| + | |||
| + | \frac{ \mathop{\rm SO} ( n) }{ \mathop{\rm SO} ( n- k) } | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | V _ {k} ( \mathbf C ^ {n} ) = U( | ||
| + | \frac{n)}{U(} | ||
| + | n- k) = | ||
| + | \frac{ \mathop{\rm SU} ( n) }{ \mathop{\rm SU} ( n- k) } | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | V _ {k} ( \mathbf H ^ {n} ) = | ||
| + | \frac{ \mathop{\rm Sp} ( n) }{ \mathop{\rm Sp} ( n- k) } | ||
| + | . | ||
| + | $$ | ||
| − | The natural quotient mapping | + | The natural quotient mapping $ O( n) \rightarrow V _ {k} ( \mathbf R ^ {n} ) $, |
| + | etc., assigns to an orthogonal, etc., matrix the $ k $- | ||
| + | frame consisting of its first $ k $ | ||
| + | columns. | ||
There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. [[Grassmann manifold|Grassmann manifold]]): | There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. [[Grassmann manifold|Grassmann manifold]]): | ||
| − | + | $$ | |
| + | V _ {k} ( E) \rightarrow \mathop{\rm Gr} _ {k} ( E) , | ||
| + | $$ | ||
| − | which assign to a | + | which assign to a $ k $- |
| + | frame the $ k $- | ||
| + | dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces: | ||
| − | + | $$ | |
| + | \mathop{\rm Gr} _ {k} ( \mathbf R ^ {n} ) = \ | ||
| + | O( | ||
| + | \frac{n)}{O(} | ||
| + | k)\times O( n- k) , | ||
| + | $$ | ||
etc. | etc. | ||
| − | Given an | + | Given an $ n $- |
| + | dimensional (real, complex, quaternionic) [[Vector bundle|vector bundle]] $ E $ | ||
| + | over a space $ X $, | ||
| + | the associated Stiefel bundles $ V _ {k} ( E) $ | ||
| + | have the fibres $ V _ {k} ( E _ {x} ) $ | ||
| + | over $ x \in X $, | ||
| + | where $ E _ {x} $ | ||
| + | is the fibre of $ E $ | ||
| + | over $ x $. | ||
| + | Similarly one has the Grassmann bundle $ \mathop{\rm Gr} _ {k} ( E) $, | ||
| + | whose fibre over $ x \in X $ | ||
| + | is the Grassmann manifold $ \mathop{\rm Gr} _ {k} ( E _ {x} ) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989)</TD></TR><TR><TD valign="top">[a3a]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777069.png" />" ''Quarterly J. Math.'' , '''7''' (1956) pp. 249–268</TD></TR><TR><TD valign="top">[a3b]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777070.png" />" ''Quarterly J. Math.'' , '''9''' (1958) pp. 8–27</TD></TR><TR><TD valign="top">[a3c]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777071.png" />" ''Quarterly J. Math.'' , '''10''' (1959) pp. 17–37; 241–260</TD></TR><TR><TD valign="top">[a3d]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777072.png" />" ''Quarterly J. Math.'' , '''11''' (1960) pp. 1–16</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989)</TD></TR><TR><TD valign="top">[a3a]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777069.png" />" ''Quarterly J. Math.'' , '''7''' (1956) pp. 249–268</TD></TR><TR><TD valign="top">[a3b]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777070.png" />" ''Quarterly J. Math.'' , '''9''' (1958) pp. 8–27</TD></TR><TR><TD valign="top">[a3c]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777071.png" />" ''Quarterly J. Math.'' , '''10''' (1959) pp. 17–37; 241–260</TD></TR><TR><TD valign="top">[a3d]</TD> <TD valign="top"> G.F. Paechter, "The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087770/s08777072.png" />" ''Quarterly J. Math.'' , '''11''' (1960) pp. 1–16</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)</TD></TR></table> | ||
Revision as of 14:55, 7 June 2020
(real)
The manifold $ V _ {n,k} $ of orthonormal $ k $- frames in an $ n $- dimensional Euclidean space. In a similar way one defines a complex Stiefel manifold $ W _ {n,k} $ and a quaternion Stiefel manifold $ X _ {n,k} $. Stiefel manifolds are compact real-analytic manifolds, and also homogeneous spaces of the classical compact groups $ O( n) $, $ U( n) $ and $ \mathop{\rm Sp} ( n) $, respectively. In particular, $ V _ {n,1} = S ^ {n-} 1 $, $ W _ {n,1} = S ^ {2n-} 1 $, $ X _ {n,1} = S ^ {4n-} 1 $ are the spheres, the Stiefel manifold $ V _ {n,2} $ is the manifold of unit vectors tangent to $ S ^ {n-} 1 $, the Stiefel manifolds $ V _ {n,n} $, $ W _ {n,n} $, $ X _ {n,n} $ are identified with the groups $ O( n) $, $ U( n) $, $ \mathop{\rm Sp} ( n) $, and $ V _ {n,n-} 1 $— with the group $ \mathop{\rm SO} ( n) $. Sometimes non-compact Stiefel manifolds, consisting of all possible $ k $- frames in $ \mathbf R ^ {n} $, $ \mathbf C ^ {n} $ or $ \mathbf H ^ {n} $, are considered.
These manifolds were introduced by E. Stiefel [1] in connection with systems of linearly independent vector fields on smooth manifolds. First started in [1], studies on the topology of Stiefel manifolds led later to the complete calculation of their cohomology rings (see [2], [3]). In particular,
$$ H ^ \star ( W _ {n,k} , \mathbf Z ) = \Lambda _ {\mathbf Z} ( x _ {2n-} 1 , x _ {2n-} 3 \dots x _ {2(} n- k)+ 1 ), $$
$$ H ^ \star ( X _ {n,k} , \mathbf Z ) = \Lambda _ {\mathbf Z} ( x _ {4n-} 1 , x _ {4n-} 5 \dots x _ {4(} n- k)+ 3 ), $$
$ H ^ \star ( V _ {n,k} , \mathbf Z _ {2} ) $ is a commutative algebra with generators $ x _ {n-} k \dots x _ {n-} 1 $ and relations
$$ x _ {i} x _ {j} = \left \{ \begin{array}{lll} x _ {i+} j & \textrm{ for } &i+ j \leq n- 1, \\ 0 & \textrm{ for } &i+ j > n- 1 \\ \end{array} \right .$$
(everywhere above, $ x _ {l} $ denotes an element of order $ l $). Real, complex and quaternion Stiefel manifolds are aspherical in dimensions not exceeding $ n- k- 1 $, $ 2( n- k) $ and $ 4( n- k)+ 2 $, respectively. Moreover,
$$ \pi _ {n-} k ( V _ {n,k} ) \cong \left \{ \begin{array}{ll} \mathbf Z & \textrm{ if } k= 1 \textrm{ or } n- k \textrm{ is even }, \\ \mathbf Z _ {2} & \textrm{ if } k> 1 \textrm{ or } n- k \textrm{ is odd } ; \\ \end{array} \right .$$
$$ \pi _ {2(} n- k)+ 1 ( W _ {n,k} ) \cong \pi _ {4(} n- k)+ 3 ( X _ {n,k} ) \cong \mathbf Z . $$
The computation of other homotopy groups of Stiefel manifolds is discussed in [5].
References
| [1] | E. Stiefel, "Richtungsfelder und Fernparallelismus in  -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 |
| [2] | A. Borel, , Fibre spaces and their applications , Moscow (1958) pp. 163–246 (In Russian; translated from French) |
| [3] | N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962) |
| [4] | V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian) |
| [5] | Itogi Nauk. Algebra. Topol. Geom. (1971) pp. 71–122 |
Comments
For homotopy groups of Stiefel manifolds see also .
Another (and better) frequently used notation for the Stiefel manifolds $ V _ {n,k } $, $ W _ {n,k } $ and $ X _ {n,k } $ is $ V _ {k} ( \mathbf R ^ {n} ) $, $ V _ {k} ( \mathbf C ^ {n} ) $, $ V _ {k} ( \mathbf H ^ {n} ) $, generalizing to $ V _ {k} ( E ) $ where $ E $ is an appropriate vector space.
As homogeneous spaces these Stiefel manifolds are equal to, respectively,
$$ V _ {k} ( \mathbf R ^ {n} ) = \ O( \frac{n)}{O(} n- k) = \ \frac{ \mathop{\rm SO} ( n) }{ \mathop{\rm SO} ( n- k) } , $$
$$ V _ {k} ( \mathbf C ^ {n} ) = U( \frac{n)}{U(} n- k) = \frac{ \mathop{\rm SU} ( n) }{ \mathop{\rm SU} ( n- k) } , $$
$$ V _ {k} ( \mathbf H ^ {n} ) = \frac{ \mathop{\rm Sp} ( n) }{ \mathop{\rm Sp} ( n- k) } . $$
The natural quotient mapping $ O( n) \rightarrow V _ {k} ( \mathbf R ^ {n} ) $, etc., assigns to an orthogonal, etc., matrix the $ k $- frame consisting of its first $ k $ columns.
There are canonical mappings from the Stiefel manifolds to the Grassmann manifolds (cf. Grassmann manifold):
$$ V _ {k} ( E) \rightarrow \mathop{\rm Gr} _ {k} ( E) , $$
which assign to a $ k $- frame the $ k $- dimensional subspace spanned by that frame. This exhibits the Grassmann manifolds as homogeneous spaces:
$$ \mathop{\rm Gr} _ {k} ( \mathbf R ^ {n} ) = \ O( \frac{n)}{O(} k)\times O( n- k) , $$
etc.
Given an $ n $- dimensional (real, complex, quaternionic) vector bundle $ E $ over a space $ X $, the associated Stiefel bundles $ V _ {k} ( E) $ have the fibres $ V _ {k} ( E _ {x} ) $ over $ x \in X $, where $ E _ {x} $ is the fibre of $ E $ over $ x $. Similarly one has the Grassmann bundle $ \mathop{\rm Gr} _ {k} ( E) $, whose fibre over $ x \in X $ is the Grassmann manifold $ \mathop{\rm Gr} _ {k} ( E _ {x} ) $.
References
| [a1] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [a2] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a3a] | G.F. Paechter, "The groups 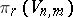 " Quarterly J. Math. , 7 (1956) pp. 249–268 " Quarterly J. Math. , 7 (1956) pp. 249–268 |
| [a3b] | G.F. Paechter, "The groups 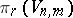 " Quarterly J. Math. , 9 (1958) pp. 8–27 " Quarterly J. Math. , 9 (1958) pp. 8–27 |
| [a3c] | G.F. Paechter, "The groups 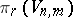 " Quarterly J. Math. , 10 (1959) pp. 17–37; 241–260 " Quarterly J. Math. , 10 (1959) pp. 17–37; 241–260 |
| [a3d] | G.F. Paechter, "The groups 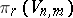 " Quarterly J. Math. , 11 (1960) pp. 1–16 " Quarterly J. Math. , 11 (1960) pp. 1–16 |
| [a4] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. 4, 78 |
| [a5] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
Stiefel manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stiefel_manifold&oldid=49604