Steinberg symbol
Let  be the group
be the group  (
( ,
,  any field). (Much of what follows holds for arbitrary simple algebraic groups, not just for
any field). (Much of what follows holds for arbitrary simple algebraic groups, not just for  .) For
.) For  ,
,  ,
,  , let
, let 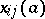 denote the element of
denote the element of 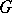 which differs from the identity matrix only in the
which differs from the identity matrix only in the 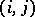 -entry, which is
-entry, which is  rather than
rather than  . The following relations hold for all
. The following relations hold for all  as above and
as above and 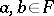 :
:
a) 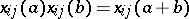 ;
;
b) 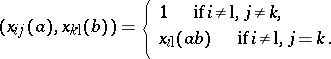 Here,
Here, 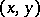 denotes the commutator
denotes the commutator 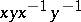 .
.
R. Steinberg [a4] proved that if 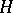 denotes the abstract group defined by these generators and relations and
denotes the abstract group defined by these generators and relations and 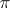 is the resulting homomorphism of
is the resulting homomorphism of  onto
onto  , then
, then 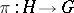 is a universal central extension of
is a universal central extension of 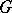 : its kernel is central and it covers all central extensions uniquely (cf. also Extension of a group). It follows that every projective representation of
: its kernel is central and it covers all central extensions uniquely (cf. also Extension of a group). It follows that every projective representation of 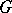 lifts uniquely to a linear representation of
lifts uniquely to a linear representation of 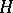 , and, at least when
, and, at least when 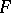 is finite, that
is finite, that  is just the Schur multiplicator of
is just the Schur multiplicator of 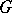 , which was the motivation for Steinberg's study.
, which was the motivation for Steinberg's study.
Now, in the group  , let
, let 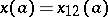 ,
, 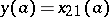 ,
, 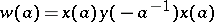 ,
, 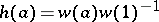 and finally
and finally 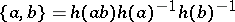 for all
for all 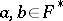 , the group of units of
, the group of units of  . Since
. Since 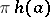 works out to the matrix
works out to the matrix 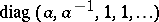 , it follows that
, it follows that 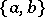 is always in
is always in 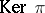 . As is mostly shown in [a4], these elements generate
. As is mostly shown in [a4], these elements generate 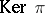 and they satisfy:
and they satisfy:
c) 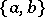 is multiplicative as a function of
is multiplicative as a function of  or of
or of  ;
;
d) 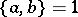 if
if 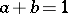 (and
(and 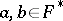 ). Matsumoto's theorem [a2] states that c) and d) form a presentation of
). Matsumoto's theorem [a2] states that c) and d) form a presentation of 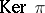 . Thus,
. Thus, 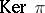 is independent of
is independent of  and hence may be (and will be) written
and hence may be (and will be) written 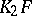 . The symbol
. The symbol  is called the Steinberg symbol, as is also any symbol in any Abelian group
is called the Steinberg symbol, as is also any symbol in any Abelian group 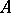 for which c) and d) hold (which corresponds to a homomorphism of
for which c) and d) hold (which corresponds to a homomorphism of 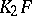 into
into  ).
).
As a first example, if  is finite, then
is finite, then  is trivial, with a few exceptions (see [a4]). Hence a) and b) form a presentation of
is trivial, with a few exceptions (see [a4]). Hence a) and b) form a presentation of 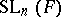 (
( ) and
) and  , as above, is an isomorphism.
, as above, is an isomorphism.
If  is a differential field, then
is a differential field, then 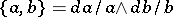 defines a symbol into
defines a symbol into 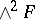 .
.
Consider next the field 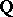 and its completions
and its completions 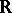 and
and 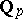 (one for each prime number
(one for each prime number 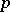 ), which are topological fields (cf. also Topological field). According to J. Tate (see [a3]),
), which are topological fields (cf. also Topological field). According to J. Tate (see [a3]),
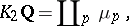 |
where 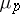 is the group of roots of unity in
is the group of roots of unity in 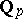 , which is cyclic, of order
, which is cyclic, of order  if
if 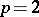 and of order
and of order  if
if 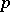 is odd. The factor for
is odd. The factor for 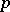 odd arises from the symbol
odd arises from the symbol 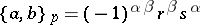 on
on 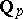 , and hence also on
, and hence also on 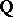 , in which
, in which 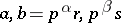 , with
, with  ,
,  units in
units in 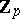 . Since
. Since 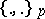 generates the group of continuous symbols on
generates the group of continuous symbols on 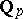 into
into  [a3], one of the interpretations of this result is that the fundamental group of
[a3], one of the interpretations of this result is that the fundamental group of 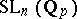 is cyclic of order
is cyclic of order 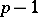 . And similarly for
. And similarly for 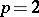 . For
. For 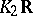 one again gets the group of roots of unity, generated by
one again gets the group of roots of unity, generated by  , which is
, which is  if
if  and
and  are both negative and is
are both negative and is  otherwise. Fitting
otherwise. Fitting 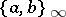 into Tate's formula above is the last step in a beautiful proof by him (see [a3]) of Gauss' quadratic reciprocity law (cf. also Quadratic reciprocity law). All of these ideas (as well as the norm residue symbol, for which c) and d) also hold) figure in a deep study of the group
into Tate's formula above is the last step in a beautiful proof by him (see [a3]) of Gauss' quadratic reciprocity law (cf. also Quadratic reciprocity law). All of these ideas (as well as the norm residue symbol, for which c) and d) also hold) figure in a deep study of the group 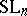 (and other groups) over arbitrary algebraic number fields and their completions initiated by C. Moore and completed by H. Matsumoto in [a2].
(and other groups) over arbitrary algebraic number fields and their completions initiated by C. Moore and completed by H. Matsumoto in [a2].
The definition of 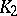 has been extended by J. Milnor [a3] to arbitrary commutative rings
has been extended by J. Milnor [a3] to arbitrary commutative rings 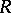 as follows. Let
as follows. Let 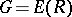 denote the group of
denote the group of  -matrices over
-matrices over 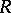 generated by the matrices
generated by the matrices  defined earlier, but with no upper bound on
defined earlier, but with no upper bound on 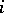 or
or 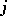 . The relations a) and b) continue to hold and they again define a universal central extension, whose kernel is called
. The relations a) and b) continue to hold and they again define a universal central extension, whose kernel is called  . The motivation comes from algebraic
. The motivation comes from algebraic  -theory, where this definition fits in well with earlier definitions of
-theory, where this definition fits in well with earlier definitions of 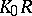 and
and 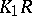 (see [a3]) via natural exact sequences, product formulas and so on. The Steinberg symbol
(see [a3]) via natural exact sequences, product formulas and so on. The Steinberg symbol 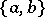 still exists, but only if
still exists, but only if  and
and 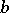 commute and are in
commute and are in 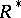 . For some rings there are enough values of
. For some rings there are enough values of 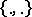 to generate
to generate 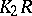 , e.g., for
, e.g., for 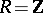 (in which case
(in which case 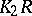 is of order
is of order  generated by
generated by 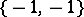 ), or for any semi-local ring or for any discrete valuation ring (in which case R.K. Dennis and M.R. Stein [a1] have given a complete set of relations, which include c) and d) above). For other rings, new symbols are needed. The Dennis–Stein symbol is defined by
), or for any semi-local ring or for any discrete valuation ring (in which case R.K. Dennis and M.R. Stein [a1] have given a complete set of relations, which include c) and d) above). For other rings, new symbols are needed. The Dennis–Stein symbol is defined by
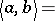 |
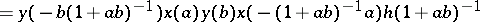 |
for all commuting pairs 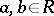 such that
such that 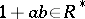 . There are various identities pertaining to
. There are various identities pertaining to  and connecting it to
and connecting it to 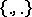 .
.
These symbols, and yet others not defined here, have been used to calculate 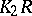 , or at least to prove that it is non-trivial, for many rings arising in
, or at least to prove that it is non-trivial, for many rings arising in 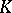 -theory, number theory, algebraic geometry, topology, and other parts of mathematics.
-theory, number theory, algebraic geometry, topology, and other parts of mathematics.
References [a1] and [a3] give good overall views of the subjects discussed.
References
| [a1] | R.K. Dennis, M.R. Stein, "The functor 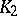 : A survey of computations and problems" , Algebraic : A survey of computations and problems" , Algebraic 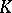 -Theory II , Lecture Notes in Mathematics , 342 , Springer (1973) pp. 243–280 -Theory II , Lecture Notes in Mathematics , 342 , Springer (1973) pp. 243–280 |
| [a2] | H. Matsumoto, "Sur les sous-groupes arithmétiques des groupes semisimples déployés" Ann. Sci. École Norm. Sup. (4) , 2 (1969) pp. 1–62 |
| [a3] | J. Milnor, "Introduction to algebraic 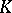 -theory" , Ann. of Math. Stud. , 72 , Princeton Univ. Press (1971) -theory" , Ann. of Math. Stud. , 72 , Princeton Univ. Press (1971) |
| [a4] | R. Steinberg, "Générateurs, relations et revêtements de groupes algébriques" , Colloq. Théorie des Groupes Algébriques (Bruxelles, 1962) , Gauthier-Villars (1962) pp. 113–127 |
Steinberg symbol. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steinberg_symbol&oldid=16963