Stefan problem
A problem that arises when studying physical processes related to phase transformation of matter. The simplest two-phase Stefan problem is formulated in thermo-physical terms as follows ([1], [2]): Find the distribution of the temperature 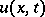 and the law of motion of the dividing boundary
and the law of motion of the dividing boundary 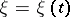 (for example, the boundary "ice-water" in freezing water) from the equation of heat conductivity:
(for example, the boundary "ice-water" in freezing water) from the equation of heat conductivity:
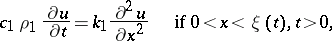 |
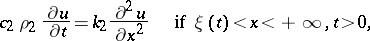 |
with the boundary condition
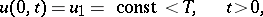 |
the initial condition
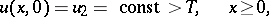 |
and the conditions on the freezing boundary
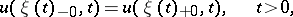 |
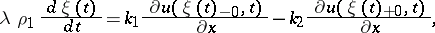 |
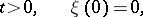 |
where 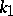 and
and 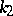 are the coefficients of heat conductivity,
are the coefficients of heat conductivity, 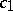 and
and 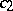 are the specific heats,
are the specific heats, 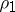 and
and 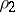 are the densities of the solid and the corresponding liquid phase,
are the densities of the solid and the corresponding liquid phase, 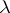 is the latent heat of melting per unit of mass, and
is the latent heat of melting per unit of mass, and 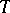 is the temperature of freezing. This problem has a self-similar solution
is the temperature of freezing. This problem has a self-similar solution 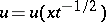 ,
, 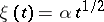 ,
, 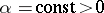 .
.
A sufficiently-general formulation of the Stefan problem in the three-dimensional spatial case reduces to a boundary value problem for a quasi-linear parabolic equation of the second order with piecewise-continuous coefficients having discontinuities of the first kind on previously-unknown but sought-for surfaces, on which the value of the required function is defined, and which also satisfy the differential Stefan condition. The existence and uniqueness of classical and generalized solutions of the Stefan problem have been studied ([3]–[6]); for methods of approximate solution of the Stefan problem, see [2], [4], [6].
One of the first to study this type of problem was J. Stefan [1].
References
| [1] | J. Stefan, "Ueber einige Probleme der Theorie der Wärmeleitung" Sitzungsber. Wiener Akad. Math. Naturwiss. Abt.  , 98 (1889) pp. 473–484 , 98 (1889) pp. 473–484 |
| [2] | A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) |
| [3] | O.A. Oleinik, "A method of solution of the general Stefan problem" Soviet Math. Dokl. , 1 : 6 (1960) pp. 1350–1354 Dokl. Akad. Nauk SSSR , 135 : 5 (1960) pp. 1054–1057 |
| [4] | B.M. Budak, A.B. Uspenskii, "A difference method with front straightening for solving Stefan-type problems" USSR Comp. Math. Math. Phys. , 9 : 6 (1969) pp. 83–103 Zh. Vychisl. Mat. i Mat. Fiz. , 9 : 6 (1969) pp. 1299–1315 |
| [5] | B.M. Budak, M.Z. Moskal, "On a classical solution of a multidimensional multiphase Stefan type problem in a domain with piecewise smooth boundary" Soviet Math. Dokl. , 13 : 2 (1970) pp. 427–432 Dokl. Akad. Nauk SSSR , 191 : 4 (1970) pp. 751–754 |
| [6] | B.M. Budak, F.P. Vasil'ev, A.B. Uspenskii, "Difference methods for solving certain boundary value problems of Stefan type" , Numerical Methods in Gas Dynamics , Moscow (1965) pp. 139–183 (In Russian) |
Comments
The problem was formulated by Stefan in [1] and [a1], but it was first studied many years before by G. Lamé and B.D. Clapeyron in a joint paper [a2].
The mathematical theory of the classical Stefan problem in one space dimension has been developed between 1947 and 1967 mainly by L. Rubinstein (see [a3]), A. Friedman (see [a4]), Jiang Li-shang, J.R. Cannon and C.D. Hill (see [a5]).
Other fundamental papers on the generalized solution of the Stefan problem are [a6]–[a8]. The reduction to a variational inequality has also received great attention [a9], [a10].
In the 1970's and 1980's many generalizations have been studied, not only concerning the conditions on the free boundary or the differential equation (see Stefan condition), but also considering the possibility of supercooling or superheating phenomena, possibly producing singularities of the solution (see e.g. [a11]–[a13]) or the occurrence of regions (called mushy regions) where the temperature is equal to the melting temperature and in which the thermal energy (or, more precisely, the enthalpy) satisfies a hyperbolic equation (see [a14]–[a16]).
Important references are also the survey papers [a17] (general theory), [a18]–[a19] (numerical methods).
The Stefan problem is related to many other free boundary problems, like the problem of gas flow through porous media (see [a20]). A useful guide to the extensive literature on the Stefan problem is [a21].
See also Differential equation, partial, free boundaries; Differential equation, partial, discontinuous coefficients; Differential equation, partial, with singular coefficients.
References
| [a1] | J. Stefan, "Ueber die Theorie der Eisbildung, insbesondere ueber die Eisbildung im Polarmeere" Ann. Physik Chemie , 42 (1891) pp. 269–286 |
| [a2] | G. Lamé, B.P. Clapeyron, "Mémoire sur la solidification par refroidissement d'un globe liquide" Ann. Chimie Physique , 47 (1831) pp. 250–256 |
| [a3] | L.I. Rubinstein, "The Stefan problem" , Amer. Math. Soc. (1971) (Translated from Russian) |
| [a4] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [a5] | J.R. Cannon, "The one-dimensional heat equation" , Addison-Wesley (1984) |
| [a6] | S.L. Kamenomostskaya, "On the Stefan problem" Mat. Sb. , 53 (1961) pp. 489–514 (In Russian) |
| [a7] | A. Friedman, "The Stefan problem in several space variables" Trans. Amer. Math. Soc. , 132 (1968) pp. 51–87 |
| [a8] | A. Friedman, "One dimensional Stefan problems with nonmonotone free boundary" Trans. Amer. Math. Soc. , 133 (1968) pp. 89–114 |
| [a9] | M. Frémond, "Variational formulation of the Stefan problem. Coupled Stefan problem - frost propagation in porous media" , Computational Methods in Nonlinear Mechanics , Univ. Texas at Austin (1974) pp. 341–349 |
| [a10] | G. Duvaut, "Résolution d'un problème de Stefan (Fusion d'un bloc de glace a zero degrées)" C.R. Acad. Sci. Paris , 276 (1973) pp. 1461–1463 |
| [a11] | A. Fasano, M. Primicerio, "New results on some classical parabolic free-bounded problems" Quart. Appl. Math. , 38 (1981) pp. 439–460 |
| [a12] | A. Fasano, M. Primicerio, "A critical case for the solvability of Stefan-like problems" Math. Methods Appl. Sci. , 5 (1983) pp. 84–96 |
| [a13] | A. Fasano, S.D. Howison, M. Primicerio, J.R. Ockendon, "On the singularities of the one-dimensional Stefan problems with supercooling" Quart. Appl. Math. (to appear) |
| [a14] | A.M. Meirmanov, "An example of nonexistence of a classical solution of the Stefan problem" Soviet Math. Dokl. , 23 (1981) pp. 564–566 Dokl. Akad. Nauk USSR , 258 : 3 (1981) pp. 547–550 |
| [a15] | M. Primicerio, "Mushy regions in phase-change problems" K.H. Hoffmann (ed.) R. Gorenflo (ed.) , Applied Nonlinear Functional analysis: Variational Methods and Ill-Posed Problems , Verlag Peter Lang (1983) pp. 251–269 |
| [a16] | A. Fasano, M. Primicerio, "A parabolic-hyperbolic free boundary problem" SIAM J. Math. Anal. , 17 (1986) pp. 67–73 |
| [a17] | M. Niezgodka, "Stefan-like problems" A. Fasano (ed.) M. Primicerio (ed.) , Free boundary problems: theory and application , 1–2 , Pitman (1983) pp. 321–348 |
| [a18] | G.H. Meyer, "Numerical methods for free boundary problems" A. Fasano (ed.) M. Primicerio (ed.) , Free boundary problems: theory and application , 1–2 , Pitman (1983) pp. 590–600 |
| [a19] | R.H. Nochetto, "Numerical solutions for free boundary problems" K.H. Hoffmann (ed.) J. Sprekels (ed.) , Free boundary problems: theory and applications , 5–6 , Longman (To appear) |
| [a20] | D.G. Aronson, "The porous medium equation" A. Fasano (ed.) M. Primicerio (ed.) , Nonlinear diffusion problems , Lect. notes in math. , 1224 , Springer (1986) pp. 1–46 |
| [a21] | D.A. Tarzia, "A bibliography on moving-free boundary problems for the heat-diffusion equation" , Prog. Naz. "Equazioni di evoluzione e applicazioni fisico-matematiche" , Firenze (1988) |
Stefan problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stefan_problem&oldid=15955