Statistical estimation
One of the fundamental parts of mathematical statistics, dedicated to the estimation using random observations of various characteristics of their distribution.
Example 1.
Let 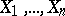 be independent random variables (or observations) with a common unknown distribution
be independent random variables (or observations) with a common unknown distribution 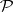 on the straight line. The empirical (sample) distribution
on the straight line. The empirical (sample) distribution 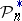 which ascribes the weight
which ascribes the weight 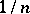 to every random point
to every random point 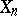 is a statistical estimator for
is a statistical estimator for 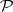 . The empirical moments
. The empirical moments
 |
serve as estimators for the moments  . In particular,
. In particular,
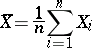 |
is an estimator for the mean, and
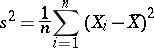 |
is an estimator for the variance.
Basic concepts.
In the general theory of estimation, an observation of 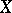 is a random element with values in a measurable space
is a random element with values in a measurable space  , whose unknown distribution belongs to a given family of distributions
, whose unknown distribution belongs to a given family of distributions 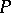 . The family of distributions can always be parametrized and written in the form
. The family of distributions can always be parametrized and written in the form 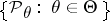 . Here the form of dependence on the parameter and the set
. Here the form of dependence on the parameter and the set  are assumed to be known. The problem of estimation using an observation
are assumed to be known. The problem of estimation using an observation 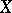 of an unknown parameter
of an unknown parameter 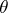 or of the value
or of the value 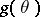 of a function
of a function 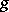 at the point
at the point 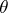 consists of constructing a function
consists of constructing a function 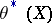 from the observations made, which gives a sufficiently good approximation of
from the observations made, which gives a sufficiently good approximation of 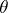
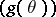 .
.
A comparison of estimators is carried out in the following way. Let a non-negative loss function 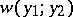 be defined on
be defined on 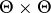
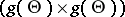 , the sense of this being that the use of
, the sense of this being that the use of 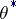 for the actual value of
for the actual value of 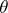 leads to losses
leads to losses 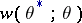 . The mean losses and the risk function
. The mean losses and the risk function 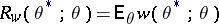 are taken as a measure of the quality of the statistic
are taken as a measure of the quality of the statistic 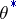 as an estimator of
as an estimator of 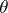 given the loss function
given the loss function 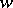 . A partial order relation is thereby introduced on the set of estimators: An estimator
. A partial order relation is thereby introduced on the set of estimators: An estimator 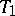 is preferable to an estimator
is preferable to an estimator 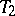 if
if 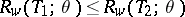 . In particular, an estimator
. In particular, an estimator 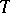 of the parameter
of the parameter 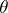 is said to be inadmissible (in relation to the loss function
is said to be inadmissible (in relation to the loss function 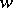 ) if an estimator
) if an estimator 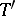 exists such that
exists such that 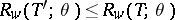 for all
for all 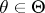 , and for some
, and for some 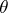 strict inequality occurs. In this method of comparing the quality of estimators, many estimators prove to be incomparable, and, moreover, the choice of a loss function is to a large extent arbitrary.
strict inequality occurs. In this method of comparing the quality of estimators, many estimators prove to be incomparable, and, moreover, the choice of a loss function is to a large extent arbitrary.
It is sometimes possible to find estimators that are optimal within a certain narrower class of estimators. Unbiased estimators form an important class. If the initial experiment is invariant relative to a certain group of transformations, it is natural to restrict to estimators that do not disrupt the symmetry of the problem (see Equivariant estimator).
Estimators can be compared by their behaviour at "worst" points: An estimator 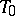 of
of 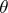 is called a minimax estimator relative to the loss function
is called a minimax estimator relative to the loss function 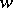 if
if
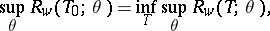 |
where the lower bound is taken over all estimators 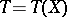 .
.
In the Bayesian formulation of the problem (cf. Bayesian approach), the unknown parameter is considered to represent values of the random variable with a priori distribution 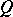 on
on  . In this case, the best estimator
. In this case, the best estimator 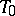 relative to the loss function
relative to the loss function 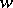 is defined by the relation
is defined by the relation
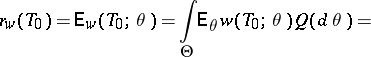 |
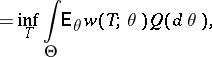 |
and the lower bound is taken over all estimators 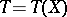 .
.
There is a distinction between parametric estimation problems, in which  is a subset of a finite-dimensional Euclidean space, and non-parametric problems. In parametric problems one usually considers loss functions in the form
is a subset of a finite-dimensional Euclidean space, and non-parametric problems. In parametric problems one usually considers loss functions in the form 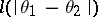 , where
, where 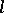 is a non-negative, non-decreasing function on
is a non-negative, non-decreasing function on 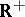 . The most frequently used quadratic loss function
. The most frequently used quadratic loss function 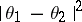 plays an important part.
plays an important part.
If 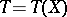 is a sufficient statistic for the family
is a sufficient statistic for the family 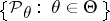 , then it is often possible to restrict to estimators
, then it is often possible to restrict to estimators 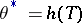 . Thus, if
. Thus, if 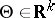 ,
, 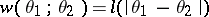 , where
, where 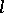 is a convex function and
is a convex function and 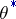 is any estimator for
is any estimator for 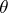 , an estimator
, an estimator 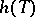 exists that is not worse than
exists that is not worse than 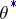 ; if
; if 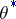 is unbiased,
is unbiased, 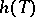 can also be chosen unbiased (Blackwell's theorem). If
can also be chosen unbiased (Blackwell's theorem). If 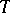 is a complete sufficient statistic for the family
is a complete sufficient statistic for the family 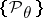 and
and  is an unbiased estimator for
is an unbiased estimator for 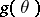 , then an unbiased estimator in the form
, then an unbiased estimator in the form 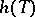 with minimum variance in the class of unbiased estimators exists (the Lehmann–Scheffé theorem).
with minimum variance in the class of unbiased estimators exists (the Lehmann–Scheffé theorem).
As a rule, it is assumed that in parametric estimation problems the elements of the family 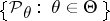 are absolutely continuous with respect to a certain
are absolutely continuous with respect to a certain 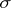 -finite measure
-finite measure 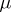 and that the density
and that the density 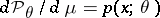 exists. If
exists. If 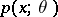 is a sufficiently-smooth function of
is a sufficiently-smooth function of 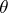 and the Fisher information matrix
and the Fisher information matrix
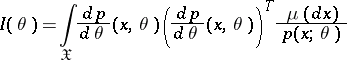 |
exists, the estimation problem is said to be regular. For regular problems, the accuracy of the estimation is bounded from below by the Cramér–Rao inequality: If 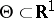 , then for any estimator
, then for any estimator 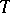 ,
,
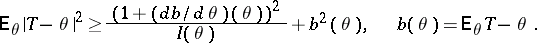 |
Examples of estimation problems 2.
The most widespread formulation is that in which a sample of size  is observed:
is observed: 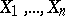 are independent identically-distributed variables taking values in a measurable space
are independent identically-distributed variables taking values in a measurable space 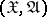 with common distribution density
with common distribution density 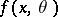 relative to a measure
relative to a measure  , and
, and 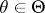 . In regular problems, if
. In regular problems, if 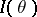 is the Fisher information on one observation, then the Fisher information of the whole sample
is the Fisher information on one observation, then the Fisher information of the whole sample 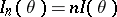 . The Cramér–Rao inequality takes the form
. The Cramér–Rao inequality takes the form
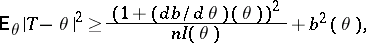 |
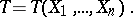 |
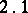 . Let
. Let 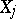 be normal random variables with distribution density
be normal random variables with distribution density
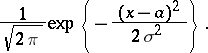 |
Let the unknown parameter be 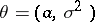 ;
; 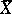 and
and 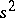 can serve as estimators for
can serve as estimators for  and
and 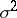 , and
, and  is then a sufficient statistic. The estimator
is then a sufficient statistic. The estimator 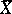 is unbiased, while
is unbiased, while 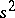 is biased. If
is biased. If 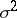 is known,
is known, 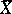 is an unbiased estimator of minimal variance, and is a minimax estimator relative to the quadratic loss function.
is an unbiased estimator of minimal variance, and is a minimax estimator relative to the quadratic loss function.
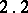 . Let
. Let 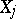 be normal random variables in
be normal random variables in 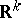 with density
with density
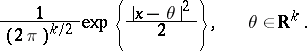 |
The statistic 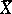 is an unbiased estimator of
is an unbiased estimator of 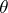 ; if
; if 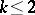 , it is admissible relative to the quadratic loss function, if
, it is admissible relative to the quadratic loss function, if 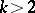 , it is inadmissible.
, it is inadmissible.
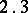 . Let
. Let 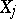 be random variables in
be random variables in  with unknown distribution density
with unknown distribution density 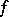 belonging to a given family
belonging to a given family 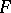 of densities. For a sufficiently broad class
of densities. For a sufficiently broad class 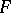 , this is a non-parametric problem. The problem of estimating
, this is a non-parametric problem. The problem of estimating 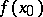 at a point
at a point 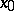 is a problem of estimating the functional
is a problem of estimating the functional  .
.
Example 3.
The linear regression model. The variables
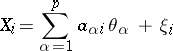 |
are observed; the  are random disturbances,
are random disturbances, 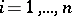 ; the matrix
; the matrix 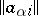 is known; and the parameter
is known; and the parameter 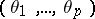 must be estimated.
must be estimated.
Example 4.
A segment of a stationary Gaussian process 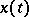 ,
, 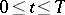 , with rational spectral density
, with rational spectral density 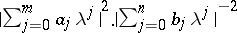 is observed; the unknown parameters
is observed; the unknown parameters 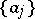 ,
, 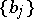 are to be estimated.
are to be estimated.
Methods of producing estimators.
The most widely used maximum-likelihood method recommends that the estimator 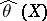 defined as the maximum point of the random function
defined as the maximum point of the random function 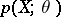 is taken, the so-called maximum-likelihood estimator. If
is taken, the so-called maximum-likelihood estimator. If 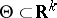 , the maximum-likelihood estimators are to be found among the roots of the likelihood equation
, the maximum-likelihood estimators are to be found among the roots of the likelihood equation
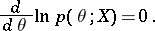 |
In example 3, the method of least squares (cf. Least squares, method of) recommends that the minimum point of the function
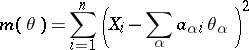 |
be used as the estimator.
Another method is to take a Bayesian estimator 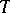 relative to a loss function
relative to a loss function 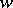 and an a priori distribution
and an a priori distribution 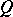 , although the initial formulation is not Bayesian. For example, if
, although the initial formulation is not Bayesian. For example, if 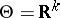 , it is possible to estimate
, it is possible to estimate 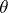 by means of
by means of
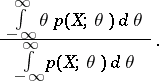 |
This is a Bayesian estimator relative to the quadratic loss function and a uniform a priori distribution.
The method of moments (cf. Moments, method of (in probability theory)) consists of the following. Let 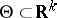 , and suppose that there are
, and suppose that there are 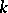 "good" estimators
"good" estimators 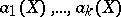 for
for 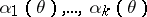 . Estimators by the method of moments are solutions of the system
. Estimators by the method of moments are solutions of the system 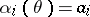 . Empirical moments are frequently chosen in the capacity of
. Empirical moments are frequently chosen in the capacity of 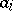 (see example 1).
(see example 1).
If the sample 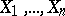 is observed, then (see example 1) as an estimator for
is observed, then (see example 1) as an estimator for 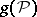 it is possible to choose
it is possible to choose  . If the function
. If the function 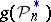 is not defined (for example,
is not defined (for example, 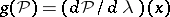 , where
, where 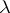 is Lebesgue measure), appropriate modifications
is Lebesgue measure), appropriate modifications 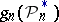 are chosen. For example, for an estimator of the density a histogram or an estimator of the form
are chosen. For example, for an estimator of the density a histogram or an estimator of the form
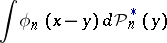 |
is used.
Asymptotic behaviour of estimators.
For the sake of being explicit a problem such as Example 2 is examined, in which 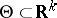 . It is to be expected that when
. It is to be expected that when 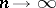 , "good" estimators will get infinitely close to the characteristic being estimated. A sequence of estimators
, "good" estimators will get infinitely close to the characteristic being estimated. A sequence of estimators  is called a consistent sequence of estimators of
is called a consistent sequence of estimators of 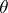 if
if 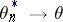 in the probability
in the probability 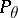 for all
for all 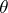 . The above methods of producing estimators lead, under broad hypotheses, to consistent estimators (cf. Consistent estimator). The estimators in example 1 are consistent. For regular estimation problems, maximum-likelihood estimators and Bayesian estimators are asymptotically normal with mean
. The above methods of producing estimators lead, under broad hypotheses, to consistent estimators (cf. Consistent estimator). The estimators in example 1 are consistent. For regular estimation problems, maximum-likelihood estimators and Bayesian estimators are asymptotically normal with mean 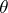 and correlation matrix
and correlation matrix 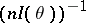 . Under such conditions, these estimators are asymptotically locally minimax relative to a broad class of loss functions, and they can be considered as being asymptotically optimal (see Asymptotically-efficient estimator).
. Under such conditions, these estimators are asymptotically locally minimax relative to a broad class of loss functions, and they can be considered as being asymptotically optimal (see Asymptotically-efficient estimator).
Interval estimation.
A random subset  of the set
of the set 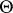 is called a confidence region for the estimator
is called a confidence region for the estimator  with confidence coefficient
with confidence coefficient 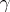 if
if  (
(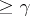 ). Many confidence regions with a given
). Many confidence regions with a given  usually exist, and the problem is to choose the one possessing certain optimal properties (for example, the interval of minimum length, if
usually exist, and the problem is to choose the one possessing certain optimal properties (for example, the interval of minimum length, if 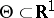 ). Under the conditions of example 2.1, let
). Under the conditions of example 2.1, let 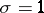 . Then the interval
. Then the interval
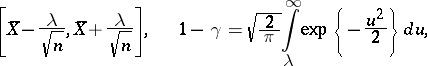 |
is a confidence interval with confidence coefficient 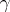 (see Interval estimator).
(see Interval estimator).
References
| [1] | R.A. Fisher, "On the mathematical foundations of theoretical statistics" Phil. Trans. Roy. Soc. London Ser. A , 222 (1922) pp. 309–368 |
| [2] | A.N. Kolmogorov, "Sur l'estimation statistique des paramètres de la loi de Gauss" Izv. Akad. Nauk SSSR Ser. Mat. , 6 : 1 (1942) pp. 3–32 |
| [3] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [4] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
| [5] | I.A. Ibragimov, R.Z. [R.Z. Khas'minskii] Has'minskii, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian) |
| [6] | N.N. Chentsov, "Statistical decision laws and optimal inference" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [7] | S. Zacks, "The theory of statistical inference" , Wiley (1975) |
| [8] | U. Grenander, "Abstract inference" , Wiley (1981) |
Comments
References
| [a1] | E.L. Lehmann, "Theory of point estimation" , Wiley (1986) |
Statistical estimation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_estimation&oldid=18593