Difference between revisions of "Stable distribution"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48797 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{MSC|60E07}} | {{MSC|60E07}} | ||
[[Category:Distribution theory]] | [[Category:Distribution theory]] | ||
| − | A probability distribution with the property that for any | + | A probability distribution with the property that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871101.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871102.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871103.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871104.png" />, the relation |
| − | |||
| − | |||
| − | |||
| − | the relation | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871105.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | holds, where | + | holds, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871106.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871107.png" /> is a certain constant, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871108.png" /> is the distribution function of the stable distribution and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s0871109.png" /> is the convolution operator for two distribution functions. |
| − | |||
| − | is a certain constant, | ||
| − | is the distribution function of the stable distribution and | ||
| − | is the convolution operator for two distribution functions. | ||
The characteristic function of a stable distribution is of the form | The characteristic function of a stable distribution is of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711010.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711014.png" /> is any real number, and |
| − | |||
| − | |||
| − | |||
| − | is any real number, and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711015.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | The number | + | The number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711016.png" /> is called the exponent of the stable distribution. A stable distribution with exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711017.png" /> is a [[Normal distribution|normal distribution]], an example of a stable distribution with exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711018.png" /> is the [[Cauchy distribution|Cauchy distribution]], a stable distribution which is a [[Degenerate distribution|degenerate distribution]] on the line. A stable distribution is an [[Infinitely-divisible distribution|infinitely-divisible distribution]]; for stable distributions with exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711020.png" />, one has the [[Lévy canonical representation|Lévy canonical representation]] with characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711021.png" />, |
| − | is called the exponent of the stable distribution. A stable distribution with exponent | ||
| − | is a [[Normal distribution|normal distribution]], an example of a stable distribution with exponent | ||
| − | is the [[Cauchy distribution|Cauchy distribution]], a stable distribution which is a [[Degenerate distribution|degenerate distribution]] on the line. A stable distribution is an [[Infinitely-divisible distribution|infinitely-divisible distribution]]; for stable distributions with exponent | ||
| − | |||
| − | one has the [[Lévy canonical representation|Lévy canonical representation]] with characteristic | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711023.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711024.png" /> is any real number. |
| − | is any real number. | ||
| − | A stable distribution, excluding the degenerate case, possesses a density. This density is infinitely differentiable, unimodal and different from zero either on the whole line or on a half-line. For a stable distribution with exponent | + | A stable distribution, excluding the degenerate case, possesses a density. This density is infinitely differentiable, unimodal and different from zero either on the whole line or on a half-line. For a stable distribution with exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711026.png" />, one has the relations |
| − | |||
| − | one has the relations | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711027.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | for | + | for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711028.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711029.png" /> is the density of the stable distribution. An explicit form of the density of a stable distribution is known only in a few cases. One of the basic problems in the theory of stable distributions is the description of their domains of attraction (cf. [[Attraction domain of a stable distribution|Attraction domain of a stable distribution]]). |
| − | where | ||
| − | is the density of the stable distribution. An explicit form of the density of a stable distribution is known only in a few cases. One of the basic problems in the theory of stable distributions is the description of their domains of attraction (cf. [[Attraction domain of a stable distribution|Attraction domain of a stable distribution]]). | ||
| − | In the set of stable distributions one singles out the set of strictly-stable distributions, for which equation (1) holds with | + | In the set of stable distributions one singles out the set of strictly-stable distributions, for which equation (1) holds with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711030.png" />. The characteristic function of a strictly-stable distribution with exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711031.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711032.png" />) is given by formula (2) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711033.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711034.png" /> a strictly-stable distribution can only be a Cauchy distribution. Spectrally-positive (negative) stable distributions are characterized by the fact that in their Lévy canonical representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711035.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711036.png" />). The Laplace transform of a spectrally-positive stable distribution exists if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711037.png" />: |
| − | The characteristic function of a strictly-stable distribution with exponent | ||
| − | |||
| − | is given by formula (2) with | ||
| − | For | ||
| − | a strictly-stable distribution can only be a Cauchy distribution. Spectrally-positive (negative) stable distributions are characterized by the fact that in their Lévy canonical representation | ||
| − | |||
| − | The Laplace transform of a spectrally-positive stable distribution exists if | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711038.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711039.png" /> is the density of the spectrally-positive stable distribution with exponent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711040.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711041.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711043.png" /> is a real number, and those branches of the many-valued functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711044.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711045.png" /> are chosen for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711046.png" /> is real and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711047.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711048.png" />. |
| − | is the density of the spectrally-positive stable distribution with exponent | ||
| − | |||
| − | |||
| − | |||
| − | is a real number, and those branches of the many-valued functions | ||
| − | |||
| − | are chosen for which | ||
| − | is real and | ||
| − | |||
| − | Stable distributions, like infinitely-divisible distributions, correspond to stationary stochastic processes with stationary independent increments. A stochastically-continuous stationary stochastic process with independent increments | + | Stable distributions, like infinitely-divisible distributions, correspond to stationary stochastic processes with stationary independent increments. A stochastically-continuous stationary stochastic process with independent increments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711049.png" /> is called stable if the increment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087110/s08711050.png" /> has a stable distribution. |
| − | is called stable if the increment | ||
| − | has a stable distribution. | ||
====References==== | ====References==== | ||
Revision as of 14:53, 7 June 2020
2020 Mathematics Subject Classification: Primary: 60E07 [MSN][ZBL]
A probability distribution with the property that for any 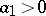 ,
, 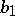 ,
, 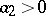 ,
, 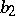 , the relation
, the relation
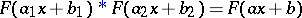 | (1) |
holds, where 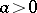 and
and 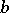 is a certain constant,
is a certain constant, 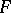 is the distribution function of the stable distribution and
is the distribution function of the stable distribution and  is the convolution operator for two distribution functions.
is the convolution operator for two distribution functions.
The characteristic function of a stable distribution is of the form
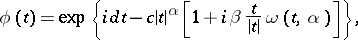 | (2) |
where 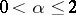 ,
, 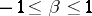 ,
,  ,
, 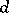 is any real number, and
is any real number, and
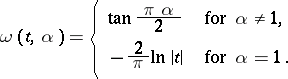 |
The number 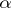 is called the exponent of the stable distribution. A stable distribution with exponent
is called the exponent of the stable distribution. A stable distribution with exponent 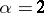 is a normal distribution, an example of a stable distribution with exponent
is a normal distribution, an example of a stable distribution with exponent 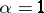 is the Cauchy distribution, a stable distribution which is a degenerate distribution on the line. A stable distribution is an infinitely-divisible distribution; for stable distributions with exponent
is the Cauchy distribution, a stable distribution which is a degenerate distribution on the line. A stable distribution is an infinitely-divisible distribution; for stable distributions with exponent 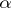 ,
, 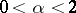 , one has the Lévy canonical representation with characteristic
, one has the Lévy canonical representation with characteristic  ,
,
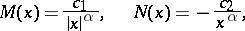 |
 |
where 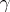 is any real number.
is any real number.
A stable distribution, excluding the degenerate case, possesses a density. This density is infinitely differentiable, unimodal and different from zero either on the whole line or on a half-line. For a stable distribution with exponent 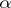 ,
, 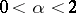 , one has the relations
, one has the relations
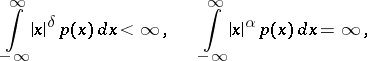 |
for 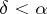 , where
, where 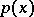 is the density of the stable distribution. An explicit form of the density of a stable distribution is known only in a few cases. One of the basic problems in the theory of stable distributions is the description of their domains of attraction (cf. Attraction domain of a stable distribution).
is the density of the stable distribution. An explicit form of the density of a stable distribution is known only in a few cases. One of the basic problems in the theory of stable distributions is the description of their domains of attraction (cf. Attraction domain of a stable distribution).
In the set of stable distributions one singles out the set of strictly-stable distributions, for which equation (1) holds with 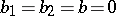 . The characteristic function of a strictly-stable distribution with exponent
. The characteristic function of a strictly-stable distribution with exponent 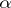 (
(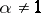 ) is given by formula (2) with
) is given by formula (2) with 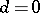 . For
. For 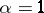 a strictly-stable distribution can only be a Cauchy distribution. Spectrally-positive (negative) stable distributions are characterized by the fact that in their Lévy canonical representation
a strictly-stable distribution can only be a Cauchy distribution. Spectrally-positive (negative) stable distributions are characterized by the fact that in their Lévy canonical representation 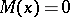 (
(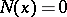 ). The Laplace transform of a spectrally-positive stable distribution exists if
). The Laplace transform of a spectrally-positive stable distribution exists if 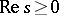 :
:
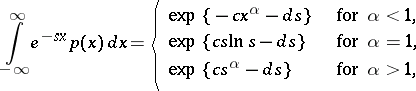 |
where 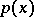 is the density of the spectrally-positive stable distribution with exponent
is the density of the spectrally-positive stable distribution with exponent 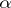 ,
, 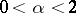 ,
, 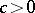 ,
, 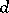 is a real number, and those branches of the many-valued functions
is a real number, and those branches of the many-valued functions 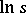 ,
, 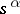 are chosen for which
are chosen for which 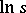 is real and
is real and 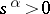 for
for 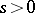 .
.
Stable distributions, like infinitely-divisible distributions, correspond to stationary stochastic processes with stationary independent increments. A stochastically-continuous stationary stochastic process with independent increments  is called stable if the increment
is called stable if the increment 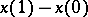 has a stable distribution.
has a stable distribution.
References
| [GK] | B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) MR0062975 Zbl 0056.36001 |
| [PR] | Yu.V. Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) MR0251754 |
| [IL] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) MR0322926 Zbl 0219.60027 |
| [S] | A.V. Skorohod, "Stochastic processes with independent increments" , Kluwer (1991) (Translated from Russian) MR0094842 |
| [Z] | V.M. Zolotarev, "One-dimensional stable distributions" , Amer. Math. Soc. (1986) (Translated from Russian) MR0854867 Zbl 0589.60015 |
Comments
In practically all the literature the characteristic function of the stable distributions contains an error of sign; for the correct formulas see [H].
References
| [H] | P. Hall, "A comedy of errors: the canonical term for the stable characteristic functions" Bull. London Math. Soc. , 13 (1981) pp. 23–27 |
Stable distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stable_distribution&oldid=49441