Sprague-Grundy function
Grundy–Sprague function, Grundy function
The function 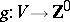 from the vertex set
from the vertex set 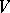 of a digraph
of a digraph 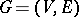 into the non-negative integers
into the non-negative integers 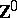 defined inductively by:
defined inductively by: 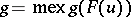 , where for any subset
, where for any subset 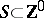 ,
, 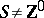 ,
, 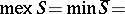 least non-negative integer not in
least non-negative integer not in 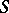 ,
, 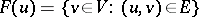 is the set of (directed) followers of
is the set of (directed) followers of  and
and 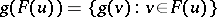 . Informally,
. Informally, 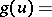 least non-negative integer not among the values
least non-negative integer not among the values 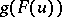 . Note that
. Note that 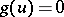 if
if  is a leaf of
is a leaf of 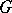 , i.e., if
, i.e., if  . In the earlier literature the function was referred to as the Grundy function, [a7]. Only later the more obscure but earlier reference [a10] became known, whence the name changed to Sprague–Grundy function, or
. In the earlier literature the function was referred to as the Grundy function, [a7]. Only later the more obscure but earlier reference [a10] became known, whence the name changed to Sprague–Grundy function, or 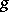 -function.
-function.
A digraph is locally walk-bounded if for every vertex 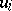 there is a bound
there is a bound 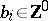 such that the length of every (directed) walk emanating from
such that the length of every (directed) walk emanating from 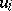 does not exceed
does not exceed 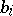 . Every locally walk-bounded digraph has a unique
. Every locally walk-bounded digraph has a unique  -function. Moreover,
-function. Moreover, 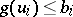 . In particular, every finite acyclic digraph has a unique
. In particular, every finite acyclic digraph has a unique 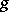 -function.
-function.
Many two-player impartial games can be described by means of their game graph (see Two-person zero-sum game), which is a digraph 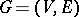 whose vertices are all the game positions, and
whose vertices are all the game positions, and 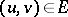 if and only if there is a legal move from position
if and only if there is a legal move from position  to position
to position  . The
. The 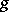 -function determines the strategy of such games if the game does not have cycles, i.e., no game position can be repeated. For a normal play, i.e., if the player making the last move wins, the connection is given by:
-function determines the strategy of such games if the game does not have cycles, i.e., no game position can be repeated. For a normal play, i.e., if the player making the last move wins, the connection is given by:
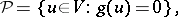 |
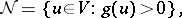 |
where 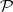 is the set of all
is the set of all  -positions of the game and
-positions of the game and 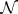 is the set of all its
is the set of all its 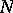 -positions. Informally, a
-positions. Informally, a 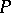 -position is any game position
-position is any game position  from which the "p" {}revious player can force a win, that is, the opponent of the player moving from
from which the "p" {}revious player can force a win, that is, the opponent of the player moving from  . An
. An  -position is any position
-position is any position  from which the "n" {}ext player can force a win, that is, the player who moves from
from which the "n" {}ext player can force a win, that is, the player who moves from  . More precisely, suppose one is given a finite or infinite game with game-graph
. More precisely, suppose one is given a finite or infinite game with game-graph 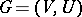 , which may be cyclic. Denote by
, which may be cyclic. Denote by 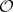 the set of all non-negative ordinals not exceeding
the set of all non-negative ordinals not exceeding 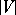 . By recursion on
. By recursion on 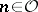 , define
, define
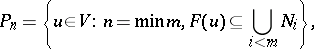 |
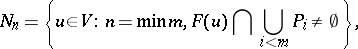 |
and 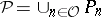 and
and 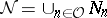 .
.
If 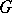 is finite, acyclic and connected, there is a depth-first
is finite, acyclic and connected, there is a depth-first 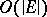 algorithm for computing
algorithm for computing 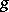 . However, there is an algorithm of the same complexity for computing
. However, there is an algorithm of the same complexity for computing 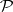 and
and 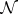 directly, so who needs
directly, so who needs 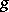 ? (Cf. also Complexity theory.)
? (Cf. also Complexity theory.)
The answer lies in the important concept of a sum of games. Let 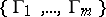 be a finite disjoint collection of games with game-graphs
be a finite disjoint collection of games with game-graphs 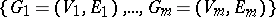 , which may have cycles or loops, or may be infinite. Then the sum-game
, which may have cycles or loops, or may be infinite. Then the sum-game 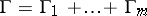 is the two-player game in which a position has the form
is the two-player game in which a position has the form 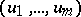 with
with 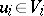 for all
for all  , and a move consists of selecting some
, and a move consists of selecting some 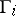 and making a legal move
and making a legal move 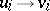 in it (
in it (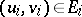 ).
).
The sum-graph 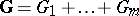 is the digraph
is the digraph  defined as follows:
defined as follows:
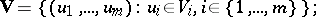 |
if 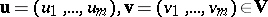 , then
, then 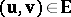 if there is some
if there is some 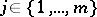 such that
such that 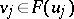 , that is,
, that is, 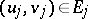 , and
, and  for all
for all 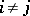 .
.
Informally, the sum of games is a game in which a move consists of selecting one of the 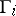 and making a move in it. For example, Nim is the sum of its heaps, and sums arise naturally in many games. The game-graph of a sum is normally exponential in the size of the
and making a move in it. For example, Nim is the sum of its heaps, and sums arise naturally in many games. The game-graph of a sum is normally exponential in the size of the 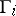 , so computing
, so computing 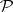 ,
, 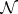 on it involves an exponential computation. But
on it involves an exponential computation. But 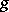 enables one to formulate a polynomial algorithm: For
enables one to formulate a polynomial algorithm: For 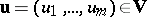 , let
, let 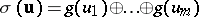 , where
, where  denotes Nim addition, also known as Xor (i.e. exclusive or), or addition over
denotes Nim addition, also known as Xor (i.e. exclusive or), or addition over 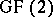 . Then
. Then 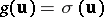 . For normal play one then has, in view of the above result,
. For normal play one then has, in view of the above result,
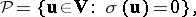 |
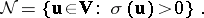 |
The polynomiality of the computation is valid for a standard game graph with input size 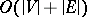 . But many of the more interesting games are succinct, i.e., have input size
. But many of the more interesting games are succinct, i.e., have input size 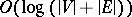 , and for them some additional property is needed to establish polynomiality. For Nim it is the fact that the
, and for them some additional property is needed to establish polynomiality. For Nim it is the fact that the 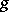 -values form an arithmetic sequence (cf. Arithmetic progression); for many octal games [a8]
-values form an arithmetic sequence (cf. Arithmetic progression); for many octal games [a8] 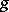 is ultimately polynomial, and for some other games special numeration systems can be exploited to recover polynomiality [a5].
is ultimately polynomial, and for some other games special numeration systems can be exploited to recover polynomiality [a5].
If the game-graph is cyclic, the game's outcome may be a draw, i.e., no player can force a win, but each has a non-losing next move. Two properties of 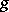 collapse when
collapse when 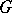 has cycles:
has cycles:
i) it may not exist or not exist uniquely; in fact, the question of the existence of  is
is 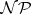 -complete [a4]; and
-complete [a4]; and
ii) it may not determine the strategy.
Fortunately, however, there is a generalized Sprague–Grundy function 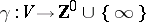 , which exists uniquely on all finite and some infinite digraphs [a9], [a3], [a2], where the symbol
, which exists uniquely on all finite and some infinite digraphs [a9], [a3], [a2], where the symbol 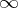 indicates a value larger than any natural number. One can define
indicates a value larger than any natural number. One can define 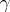 also on certain subsets of vertices. Specifically:
also on certain subsets of vertices. Specifically:
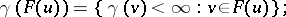 |
if 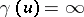 and
and 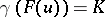 , one also writes
, one also writes 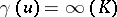 .
.
Equality of 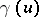 and
and 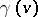 : If
: If 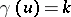 and
and 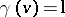 , then
, then 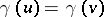 if one of the following holds:
if one of the following holds:
a) 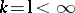 ;
;
b) 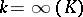 ,
, 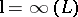 and
and 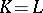 . One also uses the notations
. One also uses the notations
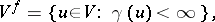 |
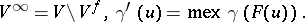 |
Further, one associates a counter function with 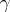 , in order to enable the winner to realize a win rather than merely maintaining a non-losing status in cycles.
, in order to enable the winner to realize a win rather than merely maintaining a non-losing status in cycles.
Given a cyclic digraph 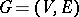 , a function
, a function 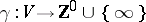 is a
is a 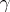 -function with counter function
-function with counter function 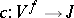 , where
, where 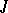 is any infinite well-ordered set, if the following three conditions hold:
is any infinite well-ordered set, if the following three conditions hold:
A) If  , then
, then 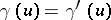 .
.
B) If 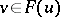 with
with 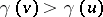 , then there exists a
, then there exists a 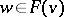 satisfying
satisfying 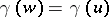 and
and 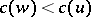 .
.
C) If 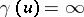 , then there is a
, then there is a 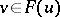 with
with 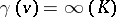 such that
such that 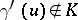 .
.
The generalized Nim-sum is defined as the Nim-sum above, augmented by:
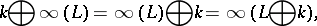 |
where  ,
, 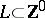 ,
, 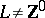 ,
, 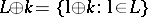 . The generalized Nim-sum of
. The generalized Nim-sum of 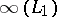 and
and 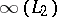 , for any subsets
, for any subsets  ,
, 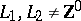 , is defined by
, is defined by
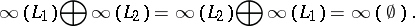 |
To handle sums of games, one sets, analogously to the above Nim addition, 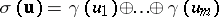 , where now
, where now  denotes generalized Nim addition. For normal play one then has
denotes generalized Nim addition. For normal play one then has
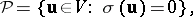 |
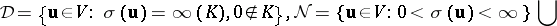 |
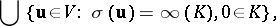 |
where 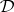 is the set of all "d" {}raw positions. For a finite connected digraph
is the set of all "d" {}raw positions. For a finite connected digraph 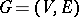 ,
, 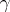 can be computed in
can be computed in 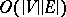 steps, which is polynomial in the size of a standard digraph.
steps, which is polynomial in the size of a standard digraph.
Many applications of the 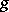 -function to games appear in [a1], and some of the results mentioned above are taken from [a6].
-function to games appear in [a1], and some of the results mentioned above are taken from [a6].
References
| [a1] | E.R. Berlekamp, J.H. Conway, R.K. Guy, "Winning ways for your mathematical plays" , I–II , Acad. Press (1982) |
| [a2] | A.S. Fraenkel, O. Rahat, "Infinite cyclic impartial games" Theoret. Computer Sci. , 252 (2001) pp. 13–22 (Special issue on Computer Games '98) |
| [a3] | A.S. Fraenkel, Y. Yesha, "Theory of annihilation games I" J. Combin. Th. B , 33 (1982) pp. 60–86 |
| [a4] | A.S. Fraenkel, "Planar kernel and Grundy with 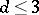 , , 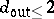 , ,  are NP-complete" Discr. Appl. Math. , 3 (1981) pp. 257–262 are NP-complete" Discr. Appl. Math. , 3 (1981) pp. 257–262 |
| [a5] | A.S. Fraenkel, "Heap games, numeration systems and sequences" Ann. Combinatorics , 2 (1998) pp. 197–210 |
| [a6] | A.S. Fraenkel, "Adventures in games and computational complexity" , Graduate Studies in Mathematics , Amer. Math. Soc. (to appear) |
| [a7] | P.M. Grundy, "Mathematics and games" Eureka , 27 (1964) pp. 9–11 (Reprint; originally: ibid. 2 (1939), 6-8) |
| [a8] | R.K. Guy, C.A.B. Smith, "The  -values of various games" Proc. Cambridge Philos. Soc. , 52 (1956) pp. 514–526 -values of various games" Proc. Cambridge Philos. Soc. , 52 (1956) pp. 514–526 |
| [a9] | C.A.B. Smith, "Graphs and composite games" J. Combin. Th. , 1 (1966) pp. 51–81 |
| [a10] | R. Sprague, "Über mathematische Kampfspiele" Tôhoku Math. J. , 41 (1935/36) pp. 438–444 |
Sprague-Grundy function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sprague-Grundy_function&oldid=19261