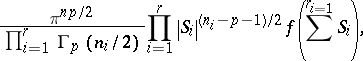|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| − | A random [[Matrix|matrix]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202301.png" /> (cf. also [[Matrix variate distribution|Matrix variate distribution]]) is said to have
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | a right spherical distribution if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202302.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202303.png" />;
| + | Out of 159 formulas, 155 were replaced by TEX code.--> |
| | | | |
| − | a left spherical distribution if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202304.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202305.png" />; and
| + | {{TEX|semi-auto}}{{TEX|part}} |
| | + | A random [[Matrix|matrix]] $X ( p \times n )$ (cf. also [[Matrix variate distribution|Matrix variate distribution]]) is said to have |
| | | | |
| − | a spherical distribution if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202306.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202307.png" /> and all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202308.png" />. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s1202309.png" /> denotes the class of orthogonal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023010.png" />-matrices (cf. also [[Orthogonal matrix|Orthogonal matrix]]). | + | a right spherical distribution if $X : = X \Lambda$ for all $\Lambda \in \mathcal{O} ( n )$; |
| | | | |
| − | Instead of saying that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023011.png" /> "has a" (left, right) spherical distribution, one also says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023012.png" /> itself is (left, right) spherical.
| + | a left spherical distribution if $X := \Gamma X$ for all $\Gamma \in \mathcal{O} ( p )$; and |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023013.png" /> is right spherical, then
| + | a spherical distribution if $X := \Gamma X \Lambda$ for all $\Gamma \in \mathcal{O} ( p )$ and all $\Lambda \in \mathcal{O} ( n )$. Here, $\mathcal{O} ( r )$ denotes the class of orthogonal $( r \times r )$-matrices (cf. also [[Orthogonal matrix|Orthogonal matrix]]). |
| | | | |
| − | a) its transpose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023014.png" /> is left spherical;
| + | Instead of saying that $X ( p \times n )$ "has a" (left, right) spherical distribution, one also says that $X ( p \times n )$ itself is (left, right) spherical. |
| | | | |
| − | b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023015.png" /> is right spherical, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023016.png" />; and
| + | If $X ( p \times n )$ is right spherical, then |
| | | | |
| − | c) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023017.png" />, its [[Characteristic function|characteristic function]] is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023018.png" />.
| + | a) its transpose $X ^ { \prime }$ is left spherical; |
| | | | |
| − | The fact that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023019.png" /> is right (left) spherical with characteristic function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023020.png" />, is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023021.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023022.png" />).
| + | b) $- X$ is right spherical, i.e. $- X := X$; and |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023023.png" />. Then:
| + | c) for $T ( p \times n )$, its [[Characteristic function|characteristic function]] is of the form $\phi ( T T ^ { \prime } )$. |
| | | | |
| − | 1) for a constant matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023025.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023027.png" />;
| + | The fact that $X ( p \times n )$ is right (left) spherical with characteristic function $\phi ( T T ^ { \prime } )$, is denoted by $X \sim \operatorname { RS } _ { p , n } ( \phi )$ (respectively, $X \sim \operatorname { LS } _ { p , n } ( \phi )$). |
| | | | |
| − | 2) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023028.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023029.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023030.png" />-matrix, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023031.png" />;
| + | Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$. Then: |
| | | | |
| − | 3) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023032.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023033.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023034.png" />, the [[Uniform distribution|uniform distribution]] on the [[Stiefel manifold|Stiefel manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023035.png" />.
| + | 1) for a constant matrix $A ( q \times p )$, $A X \sim \operatorname { RS } _ { q , n } ( \psi )$, where $\psi ( T T ^ { \prime } ) = \phi ( A ^ { \prime } T T ^ { \prime } A )$, $T ( q \times n )$; |
| | | | |
| − | The [[Probability distribution|probability distribution]] of a right spherical matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023036.png" /> is fully determined by that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023037.png" />. It follows that the uniform distribution is the unique right spherical distribution over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023038.png" />. For a right spherical matrix the density need not exist in general. However, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023039.png" /> has a density with respect to [[Lebesgue measure|Lebesgue measure]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023040.png" />, then it is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023041.png" />. | + | 2) for $X = ( X _ { 1 } , X _ { 2 } )$, where $X _ { 1 }$ is a $( p \times m )$-matrix, $X _ { 1 } \sim \operatorname { RS } _ { p , m } ( \phi )$; |
| | + | |
| | + | 3) if $X X ^ { \prime } = I _ { p }$, $p \leq n$, then $X \sim \mathcal{U} _ { p , n}$, the [[Uniform distribution|uniform distribution]] on the [[Stiefel manifold|Stiefel manifold]] $\mathcal{O} ( p , n ) = \{ H ( p \times n ) : H H ^ { \prime } = I _ { p } \}$. |
| | + | |
| | + | The [[Probability distribution|probability distribution]] of a right spherical matrix $X ( p \times n )$ is fully determined by that of $X X ^ { \prime }$. It follows that the uniform distribution is the unique right spherical distribution over $\mathcal{O} ( p , n )$. For a right spherical matrix the density need not exist in general. However, if $X$ has a density with respect to [[Lebesgue measure|Lebesgue measure]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023040.png"/>, then it is of the form $f ( X X ^ { \prime } )$. |
| | | | |
| | ==Examples of spherical distributions with a density.== | | ==Examples of spherical distributions with a density.== |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023042.png" />, the density of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023043.png" /> is | + | When $X \sim N _ { p , n } ( 0 , \Sigma \otimes I _ { n } )$, the density of $X$ is |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023044.png" /></td> </tr></table>
| + | \begin{equation*} \frac { 1 } { ( 2 \pi ) ^ { n p / 2 } } | \Sigma | ^ { - n / 2 } \operatorname { etr } \left\{ - \frac { 1 } { 2 } \Sigma ^ { - 1 } X X ^ { \prime } \right\} , X \in \mathbf{R} ^ { p \times n }, \end{equation*} |
| | | | |
| | with characteristic function | | with characteristic function |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023045.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { etr } \left\{ - \frac { 1 } { 2 } \Sigma ^ { - 1 } T T ^ { \prime } \right\}. \end{equation*} |
| | | | |
| − | Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023046.png" /> is the exponential trace function: | + | Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023046.png"/> is the exponential trace function: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023047.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { etr } ( A ) = \operatorname { exp } ( \operatorname { tr } ( A ) ). \end{equation*} |
| | | | |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023048.png" />, the density of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023049.png" /> is | + | When $X \sim T _ { p , n } ( \delta , 0 , \Sigma , I _ { n } )$, the density of $X$ is |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023050.png" /></td> </tr></table>
| + | \begin{equation*} \frac { \Gamma _ { p } \left[ \frac { \delta + n + p - 1 } { 2 } \right] } { ( 2 \pi ) ^ { n p / 2 } | \Sigma | ^ { n / 2 } \Gamma _ { p } \left[ \frac { \delta + p - 1 } { 2 } \right] }. \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023051.png" /></td> </tr></table>
| + | \begin{equation*} .\left| I _ { p } + \Sigma ^ { - 1 } X X ^ { \prime } \right| ^ { - ( \delta + n + p - 1 ) / 2 } , X \in \mathbf{R} ^ { p \times n }, \end{equation*} |
| | | | |
| | with characteristic function | | with characteristic function |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023052.png" /></td> </tr></table>
| + | \begin{equation*} \frac { B _ { - ( \delta + p - 1 ) / 2} \left( \frac { 1 } { 4 } \Sigma T T ^ { \prime } \right) } { \Gamma _ { p } \left[ \frac { 1 } { 2 } ( \delta + p - 1 ) \right] }, \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023053.png" /> is Herz's Bessel function of the second kind and of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023054.png" />. | + | where $B _ { \delta } ( \cdot )$ is Herz's Bessel function of the second kind and of order $\delta$. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023055.png" /> is right spherical and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023056.png" /> is a fixed matrix, then the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023057.png" /> depends on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023058.png" /> only through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023059.png" />. Now, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023060.png" />, then the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023061.png" /> is right spherical. | + | If $X ( p \times n )$ is right spherical and $K ( n \times m )$ is a fixed matrix, then the distribution of $X K$ depends on $K$ only through $K ^ { \prime } K$. Now, if $K ^ { \prime } K = I _ { m }$, then the distribution of $X K$ is right spherical. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023062.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023063.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023064.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023065.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023067.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023068.png" />, and therefore <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023069.png" /> is right spherical. | + | Let $X = ( X _ { 1 } , X _ { 2 } )$, with $X _ { 1 } ( p \times ( n - m ) )$, $X _ { 2 } ( p \times m )$, and let $K ^ { \prime } = ( K _ { 1 } ^ { \prime } , K _ { 2 } ^ { \prime } )$, where $K _ { 1 } ( ( n - m ) \times m ) = 0$, $K _ { 2 } ( m \times m ) = I _ { m }$. Then $K ^ { \prime } K = I _ { m }$, and therefore $X K = X _ { 2 }$ is right spherical. |
| | | | |
| − | If the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023070.png" /> is a mixture of right spherical distributions, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023071.png" /> is right spherical. It follows that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023072.png" />, conditional on a [[Random variable|random variable]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023073.png" />, is right spherical and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023074.png" /> is a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023075.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023076.png" /> is right spherical. | + | If the distribution of $X$ is a mixture of right spherical distributions, then $X$ is right spherical. It follows that if $X ( p \times n )$, conditional on a [[Random variable|random variable]] $v$, is right spherical and $Q ( q \times p )$ is a function of $v$, then $Q X$ is right spherical. |
| | | | |
| | The results given above have obvious analogues for left spherical distributions. | | The results given above have obvious analogues for left spherical distributions. |
| | | | |
| | ==Stochastic representation of spherical distributions.== | | ==Stochastic representation of spherical distributions.== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023077.png" />. Then there exists a random matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023078.png" /> such that | + | Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$. Then there exists a random matrix $A ( p \times p )$ such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023079.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table>
| + | \begin{equation} \tag{a1} X : = A U, \end{equation} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023080.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023081.png" />. | + | where $U \sim \mathcal{U} _ { p , n }$ is independent of $A$. |
| | | | |
| − | The matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023082.png" /> in the stochastic representation (a1) is not unique. One can take it to be a lower (upper) triangular matrix with non-negative diagonal elements or a right spherical matrix with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023083.png" />. Further, if it is additionally assumed that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023084.png" />, then the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023085.png" /> is unique. | + | The matrix $A$ in the stochastic representation (a1) is not unique. One can take it to be a lower (upper) triangular matrix with non-negative diagonal elements or a right spherical matrix with $A \geq 0$. Further, if it is additionally assumed that $\mathsf P ( | XX ^ { \prime } | = 0 ) = 0$, then the distribution of $A$ is unique. |
| | | | |
| − | Given the assumption that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023086.png" /> is lower triangular in the above representation, one can prove that it is unique. Indeed, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023087.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023088.png" />. Then for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023089.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023090.png" /> lower triangular matrices with positive diagonal elements and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023092.png" />: | + | Given the assumption that $A$ is lower triangular in the above representation, one can prove that it is unique. Indeed, let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ and $\mathsf{P} ( | XX ^ { \prime } | \neq 0 ) = 1$. Then for $A$, $B$ lower triangular matrices with positive diagonal elements and $U \sim \mathcal{U} _ { p , n }$, $Q \sim \mathcal{U} _ { p , n }$: |
| | | | |
| − | i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023093.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023094.png" />; | + | i) $X : = A U$ and $X = B U \Rightarrow A : = B$; |
| | | | |
| − | ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023095.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023096.png" />. | + | ii) $X : = A U$ and $X : = A Q \Rightarrow U : = Q$. |
| | | | |
| − | For studying the spherical distribution, [[singular value decomposition]] of the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023097.png" /> provides a powerful tool. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023098.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s12023099.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230100.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230101.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230102.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230103.png" />, and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230104.png" /> are the eigenvalues of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230105.png" />. | + | For studying the spherical distribution, [[singular value decomposition]] of the matrix $X ( p \times n )$ provides a powerful tool. When $p \leq n$, let $X = G \Lambda H$, where $G \in \mathcal{O} ( p )$, $H \in \mathcal{O} ( p , n )$, $\Lambda = \operatorname { diag } ( \lambda _ { 1 } , \dots , \lambda _ { p } )$, $\lambda _ { 1 } \geq \ldots \geq \lambda _ { p } \geq 0$, and the $\lambda _ { i }$ are the eigenvalues of $( X X ^ { \prime } ) ^ { 1 / 2 }$. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230106.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230107.png" />, is spherical, then | + | If $X ( p \times n )$, $p \leq n$, is spherical, then |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230108.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table>
| + | \begin{equation} \tag{a2} X : = U \Lambda V, \end{equation} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230110.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230111.png" /> are mutually independent. | + | where $U \sim \mathcal U _ { p , p }$, $V \sim {\cal U} _ { p , n }$ and $\Lambda$ are mutually independent. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230112.png" /> is spherical, then its characteristic function is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230113.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230114.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230115.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230116.png" /> are the eigenvalues of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230117.png" />. | + | If $X ( p \times n )$ is spherical, then its characteristic function is of the form $\phi ( \lambda ( T T ^ { \prime } ) )$, where $T ( p \times n )$, $\lambda ( T T ^ { \prime } ) = \operatorname { diag } ( \tau _ { 1 } , \dots , \tau _ { 1 } )$, and $\tau _ { 1 } \geq \ldots \geq \tau _ { p } \geq 0$ are the eigenvalues of $TT'$. |
| | | | |
| − | From the above it follows that, if the density of a spherical matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230118.png" /> exists, then it is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230119.png" />. | + | From the above it follows that, if the density of a spherical matrix $X$ exists, then it is of the form $f ( \lambda ( X X ^ { \prime } ) )$. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230120.png" />. If the second-order moments of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230121.png" /> exist (cf. also [[Moment|Moment]]), then | + | Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$. If the second-order moments of $X$ exist (cf. also [[Moment|Moment]]), then |
| | | | |
| − | i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230122.png" />; | + | i) $\mathsf{E} ( X ) = 0$; |
| | | | |
| − | ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230123.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230124.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230125.png" />. | + | ii) $\operatorname { cov } ( X ) = V \otimes I _ { n }$, where $V = \mathsf{E} ( {\bf x} _ { 1 } {\bf x} _ { 1 } ^ { \prime } )$, $X = ( \mathbf{x} _ { 1 } , \dots , \mathbf{x} _ { n } )$. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230126.png" /> with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230127.png" />. Then the density of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230128.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230129.png" />, is | + | Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ with density $f ( X X ^ { \prime } )$. Then the density of $S = X X ^ { \prime }$, $n \geq p$, is |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230130.png" /></td> </tr></table>
| + | \begin{equation*} \frac { \pi ^ { n p / 2 } } { \Gamma _ { p } ( n / 2 ) } | S | ^ { ( n - p - 1 ) / 2 } f ( S ) , \quad S > 0. \end{equation*} |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230131.png" /> with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230132.png" />. Partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230133.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230134.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230135.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230136.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230137.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230138.png" />. Define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230139.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230140.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230141.png" /> with probability density function | + | Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ with density $f ( X X ^ { \prime } )$. Partition $X$ as $X = ( X _ { 1 } , \dots , X _ { r } )$, $X _ { i } ( p \times n _ { i } )$, $n _ { i } \geq p$, $ i = 1 , \ldots , r$, $\sum _ { i = 1 } ^ { r } n _ { i } = n$. Define $S _ { i } = X _ { i } X_i ^ { \prime }$, $ i = 1 , \ldots , r$. Then $( S _ { 1 } , \dots , S _ { r } ) \sim L _ { r } ^ { ( 1 ) } ( f , n _ { 1 } / 2 , \dots , n _ { r } / 2 )$ with probability density function |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230142.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230142.png"/></td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230143.png" /></td> </tr></table>
| + | \begin{equation*} S _ { i } > 0 , i = 1 , \dots , r. \end{equation*} |
| | | | |
| − | The above result has been generalized further. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230144.png" /> with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230145.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230146.png" /> be a [[Symmetric matrix|symmetric matrix]]. Then | + | The above result has been generalized further. Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ with density $f ( X X ^ { \prime } )$, and let $A ( n \times n )$ be a [[Symmetric matrix|symmetric matrix]]. Then |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230147.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a3)</td></tr></table>
| + | \begin{equation} \tag{a3} X A X ^ { \prime } \sim L _ { 1 } ^ { ( 1 ) } \left( f _ { 1 } , \frac { { k } } { 2 } \right), \end{equation} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230148.png" /> is the Weyl fractional integral of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230149.png" /> (cf. also [[Fractional integration and differentiation|Fractional integration and differentiation]]), if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230150.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230151.png" />. Further, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230152.png" /> be symmetric matrices. Then | + | where $f _ { 1 } ( T ) = W ^ { ( n - k ) / 2 } f ( T )$ is the Weyl fractional integral of order $( n - k ) / 2$ (cf. also [[Fractional integration and differentiation|Fractional integration and differentiation]]), if and only if $A ^ { 2 } = A$ and $\text{rank} ( A ) = k \geq p$. Further, let $A _ { 1 } ( n \times n ) , \dots , A _ { s } ( n \times n )$ be symmetric matrices. Then |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230153.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a4)</td></tr></table>
| + | \begin{equation} \tag{a4} \left( X A _ { 1 } X ^ { \prime } , \ldots , X A _ { s } X ^ { \prime } ) \sim L _ { s } ^ { ( 1 ) } ( f _ { 1 } , \frac { n _ { 1 } } { 2 } , \dots , \frac { n _ { s } } { 2 } \right), \end{equation} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230154.png" />, if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230155.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230156.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230157.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120230/s120230158.png" />. | + | where $f _ { 1 } ( T ) = W ^ { ( n - n _ { 1 } - \ldots - n _ { s } ) / 2 } f ( T )$, if and only if $A _ { i } A _ { j } = \delta _ { i j } A$, and $\operatorname{rank} ( A _ { i } ) = n_i$, $n _ { i } \geq p$, $i,j = 1 , \dots , s$. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.P. Dawid, "Spherical matrix distributions and multivariate model" ''J. R. Statist. Soc. Ser. B'' , '''39''' (1977) pp. 254–261</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K.T. Fang, Y.T. Zhang, "Generalized multivariate analysis" , Springer (1990)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A.P. Dawid, "Spherical matrix distributions and multivariate model" ''J. R. Statist. Soc. Ser. B'' , '''39''' (1977) pp. 254–261</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> K.T. Fang, Y.T. Zhang, "Generalized multivariate analysis" , Springer (1990)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993)</td></tr></table> |
A random matrix $X ( p \times n )$ (cf. also Matrix variate distribution) is said to have
a right spherical distribution if $X : = X \Lambda$ for all $\Lambda \in \mathcal{O} ( n )$;
a left spherical distribution if $X := \Gamma X$ for all $\Gamma \in \mathcal{O} ( p )$; and
a spherical distribution if $X := \Gamma X \Lambda$ for all $\Gamma \in \mathcal{O} ( p )$ and all $\Lambda \in \mathcal{O} ( n )$. Here, $\mathcal{O} ( r )$ denotes the class of orthogonal $( r \times r )$-matrices (cf. also Orthogonal matrix).
Instead of saying that $X ( p \times n )$ "has a" (left, right) spherical distribution, one also says that $X ( p \times n )$ itself is (left, right) spherical.
If $X ( p \times n )$ is right spherical, then
a) its transpose $X ^ { \prime }$ is left spherical;
b) $- X$ is right spherical, i.e. $- X := X$; and
c) for $T ( p \times n )$, its characteristic function is of the form $\phi ( T T ^ { \prime } )$.
The fact that $X ( p \times n )$ is right (left) spherical with characteristic function $\phi ( T T ^ { \prime } )$, is denoted by $X \sim \operatorname { RS } _ { p , n } ( \phi )$ (respectively, $X \sim \operatorname { LS } _ { p , n } ( \phi )$).
Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$. Then:
1) for a constant matrix $A ( q \times p )$, $A X \sim \operatorname { RS } _ { q , n } ( \psi )$, where $\psi ( T T ^ { \prime } ) = \phi ( A ^ { \prime } T T ^ { \prime } A )$, $T ( q \times n )$;
2) for $X = ( X _ { 1 } , X _ { 2 } )$, where $X _ { 1 }$ is a $( p \times m )$-matrix, $X _ { 1 } \sim \operatorname { RS } _ { p , m } ( \phi )$;
3) if $X X ^ { \prime } = I _ { p }$, $p \leq n$, then $X \sim \mathcal{U} _ { p , n}$, the uniform distribution on the Stiefel manifold $\mathcal{O} ( p , n ) = \{ H ( p \times n ) : H H ^ { \prime } = I _ { p } \}$.
The probability distribution of a right spherical matrix $X ( p \times n )$ is fully determined by that of $X X ^ { \prime }$. It follows that the uniform distribution is the unique right spherical distribution over $\mathcal{O} ( p , n )$. For a right spherical matrix the density need not exist in general. However, if $X$ has a density with respect to Lebesgue measure on 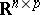 , then it is of the form $f ( X X ^ { \prime } )$.
, then it is of the form $f ( X X ^ { \prime } )$.
Examples of spherical distributions with a density.
When $X \sim N _ { p , n } ( 0 , \Sigma \otimes I _ { n } )$, the density of $X$ is
\begin{equation*} \frac { 1 } { ( 2 \pi ) ^ { n p / 2 } } | \Sigma | ^ { - n / 2 } \operatorname { etr } \left\{ - \frac { 1 } { 2 } \Sigma ^ { - 1 } X X ^ { \prime } \right\} , X \in \mathbf{R} ^ { p \times n }, \end{equation*}
with characteristic function
\begin{equation*} \operatorname { etr } \left\{ - \frac { 1 } { 2 } \Sigma ^ { - 1 } T T ^ { \prime } \right\}. \end{equation*}
Here, 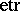 is the exponential trace function:
is the exponential trace function:
\begin{equation*} \operatorname { etr } ( A ) = \operatorname { exp } ( \operatorname { tr } ( A ) ). \end{equation*}
When $X \sim T _ { p , n } ( \delta , 0 , \Sigma , I _ { n } )$, the density of $X$ is
\begin{equation*} \frac { \Gamma _ { p } \left[ \frac { \delta + n + p - 1 } { 2 } \right] } { ( 2 \pi ) ^ { n p / 2 } | \Sigma | ^ { n / 2 } \Gamma _ { p } \left[ \frac { \delta + p - 1 } { 2 } \right] }. \end{equation*}
\begin{equation*} .\left| I _ { p } + \Sigma ^ { - 1 } X X ^ { \prime } \right| ^ { - ( \delta + n + p - 1 ) / 2 } , X \in \mathbf{R} ^ { p \times n }, \end{equation*}
with characteristic function
\begin{equation*} \frac { B _ { - ( \delta + p - 1 ) / 2} \left( \frac { 1 } { 4 } \Sigma T T ^ { \prime } \right) } { \Gamma _ { p } \left[ \frac { 1 } { 2 } ( \delta + p - 1 ) \right] }, \end{equation*}
where $B _ { \delta } ( \cdot )$ is Herz's Bessel function of the second kind and of order $\delta$.
If $X ( p \times n )$ is right spherical and $K ( n \times m )$ is a fixed matrix, then the distribution of $X K$ depends on $K$ only through $K ^ { \prime } K$. Now, if $K ^ { \prime } K = I _ { m }$, then the distribution of $X K$ is right spherical.
Let $X = ( X _ { 1 } , X _ { 2 } )$, with $X _ { 1 } ( p \times ( n - m ) )$, $X _ { 2 } ( p \times m )$, and let $K ^ { \prime } = ( K _ { 1 } ^ { \prime } , K _ { 2 } ^ { \prime } )$, where $K _ { 1 } ( ( n - m ) \times m ) = 0$, $K _ { 2 } ( m \times m ) = I _ { m }$. Then $K ^ { \prime } K = I _ { m }$, and therefore $X K = X _ { 2 }$ is right spherical.
If the distribution of $X$ is a mixture of right spherical distributions, then $X$ is right spherical. It follows that if $X ( p \times n )$, conditional on a random variable $v$, is right spherical and $Q ( q \times p )$ is a function of $v$, then $Q X$ is right spherical.
The results given above have obvious analogues for left spherical distributions.
Stochastic representation of spherical distributions.
Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$. Then there exists a random matrix $A ( p \times p )$ such that
\begin{equation} \tag{a1} X : = A U, \end{equation}
where $U \sim \mathcal{U} _ { p , n }$ is independent of $A$.
The matrix $A$ in the stochastic representation (a1) is not unique. One can take it to be a lower (upper) triangular matrix with non-negative diagonal elements or a right spherical matrix with $A \geq 0$. Further, if it is additionally assumed that $\mathsf P ( | XX ^ { \prime } | = 0 ) = 0$, then the distribution of $A$ is unique.
Given the assumption that $A$ is lower triangular in the above representation, one can prove that it is unique. Indeed, let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ and $\mathsf{P} ( | XX ^ { \prime } | \neq 0 ) = 1$. Then for $A$, $B$ lower triangular matrices with positive diagonal elements and $U \sim \mathcal{U} _ { p , n }$, $Q \sim \mathcal{U} _ { p , n }$:
i) $X : = A U$ and $X = B U \Rightarrow A : = B$;
ii) $X : = A U$ and $X : = A Q \Rightarrow U : = Q$.
For studying the spherical distribution, singular value decomposition of the matrix $X ( p \times n )$ provides a powerful tool. When $p \leq n$, let $X = G \Lambda H$, where $G \in \mathcal{O} ( p )$, $H \in \mathcal{O} ( p , n )$, $\Lambda = \operatorname { diag } ( \lambda _ { 1 } , \dots , \lambda _ { p } )$, $\lambda _ { 1 } \geq \ldots \geq \lambda _ { p } \geq 0$, and the $\lambda _ { i }$ are the eigenvalues of $( X X ^ { \prime } ) ^ { 1 / 2 }$.
If $X ( p \times n )$, $p \leq n$, is spherical, then
\begin{equation} \tag{a2} X : = U \Lambda V, \end{equation}
where $U \sim \mathcal U _ { p , p }$, $V \sim {\cal U} _ { p , n }$ and $\Lambda$ are mutually independent.
If $X ( p \times n )$ is spherical, then its characteristic function is of the form $\phi ( \lambda ( T T ^ { \prime } ) )$, where $T ( p \times n )$, $\lambda ( T T ^ { \prime } ) = \operatorname { diag } ( \tau _ { 1 } , \dots , \tau _ { 1 } )$, and $\tau _ { 1 } \geq \ldots \geq \tau _ { p } \geq 0$ are the eigenvalues of $TT'$.
From the above it follows that, if the density of a spherical matrix $X$ exists, then it is of the form $f ( \lambda ( X X ^ { \prime } ) )$.
Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$. If the second-order moments of $X$ exist (cf. also Moment), then
i) $\mathsf{E} ( X ) = 0$;
ii) $\operatorname { cov } ( X ) = V \otimes I _ { n }$, where $V = \mathsf{E} ( {\bf x} _ { 1 } {\bf x} _ { 1 } ^ { \prime } )$, $X = ( \mathbf{x} _ { 1 } , \dots , \mathbf{x} _ { n } )$.
Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ with density $f ( X X ^ { \prime } )$. Then the density of $S = X X ^ { \prime }$, $n \geq p$, is
\begin{equation*} \frac { \pi ^ { n p / 2 } } { \Gamma _ { p } ( n / 2 ) } | S | ^ { ( n - p - 1 ) / 2 } f ( S ) , \quad S > 0. \end{equation*}
Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ with density $f ( X X ^ { \prime } )$. Partition $X$ as $X = ( X _ { 1 } , \dots , X _ { r } )$, $X _ { i } ( p \times n _ { i } )$, $n _ { i } \geq p$, $ i = 1 , \ldots , r$, $\sum _ { i = 1 } ^ { r } n _ { i } = n$. Define $S _ { i } = X _ { i } X_i ^ { \prime }$, $ i = 1 , \ldots , r$. Then $( S _ { 1 } , \dots , S _ { r } ) \sim L _ { r } ^ { ( 1 ) } ( f , n _ { 1 } / 2 , \dots , n _ { r } / 2 )$ with probability density function
\begin{equation*} S _ { i } > 0 , i = 1 , \dots , r. \end{equation*}
The above result has been generalized further. Let $X \sim \operatorname { RS } _ { p , n } ( \phi )$ with density $f ( X X ^ { \prime } )$, and let $A ( n \times n )$ be a symmetric matrix. Then
\begin{equation} \tag{a3} X A X ^ { \prime } \sim L _ { 1 } ^ { ( 1 ) } \left( f _ { 1 } , \frac { { k } } { 2 } \right), \end{equation}
where $f _ { 1 } ( T ) = W ^ { ( n - k ) / 2 } f ( T )$ is the Weyl fractional integral of order $( n - k ) / 2$ (cf. also Fractional integration and differentiation), if and only if $A ^ { 2 } = A$ and $\text{rank} ( A ) = k \geq p$. Further, let $A _ { 1 } ( n \times n ) , \dots , A _ { s } ( n \times n )$ be symmetric matrices. Then
\begin{equation} \tag{a4} \left( X A _ { 1 } X ^ { \prime } , \ldots , X A _ { s } X ^ { \prime } ) \sim L _ { s } ^ { ( 1 ) } ( f _ { 1 } , \frac { n _ { 1 } } { 2 } , \dots , \frac { n _ { s } } { 2 } \right), \end{equation}
where $f _ { 1 } ( T ) = W ^ { ( n - n _ { 1 } - \ldots - n _ { s } ) / 2 } f ( T )$, if and only if $A _ { i } A _ { j } = \delta _ { i j } A$, and $\operatorname{rank} ( A _ { i } ) = n_i$, $n _ { i } \geq p$, $i,j = 1 , \dots , s$.
References
| [a1] | A.P. Dawid, "Spherical matrix distributions and multivariate model" J. R. Statist. Soc. Ser. B , 39 (1977) pp. 254–261 |
| [a2] | K.T. Fang, Y.T. Zhang, "Generalized multivariate analysis" , Springer (1990) |
| [a3] | A.K. Gupta, T. Varga, "Elliptically contoured models in statistics" , Kluwer Acad. Publ. (1993) |
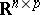 , then it is of the form $f ( X X ^ { \prime } )$.
, then it is of the form $f ( X X ^ { \prime } )$.
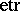 is the exponential trace function:
is the exponential trace function: